As you guys may notice, there is a big gap between Div1C and Div1D. We apologize for our inaccurate measure of the difficulty of Div1 D and Div1F1. In fact, many testers solved this problem during their VP. I think it's because CNOIers trained such kind of problems more, I mean combinatorics and counting. As you can see this round contains a lot of math things, Div1 DEF really sound like math problems. Previously, we think problems should more like this (math, finding lemma, observation) rather than graph+data structures+strings. This is because we want to do something new. In peoples mind, CN rounds usually means data structures+(graph/string/FFT) which is not interesting at all.
I discovered that many participants asked about Div2B. Honestly, I was confused as well when I was testing the round. I told this to the author but later we decide to keep that discription. This ended up in a big trouble which we haven't thought about before.
There are also some problems about the test data. System test is not strong enough and some strange code passed the final test. We notice this by checking 3 suspicious challenges. It turns out that the reason it that only the author of each problem made the data of his problem.
We will design more contests in the future. And we will try to avoid these problems. If you have anything that you want to say to us or any uncomfortable experience you encountered during the contest, just let us know.








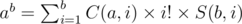
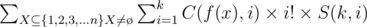
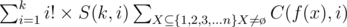
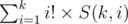 we can use the following
we can use the following 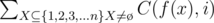 we use tree DP. Let's define
we use tree DP. Let's define 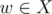 for every selected edge
for every selected edge