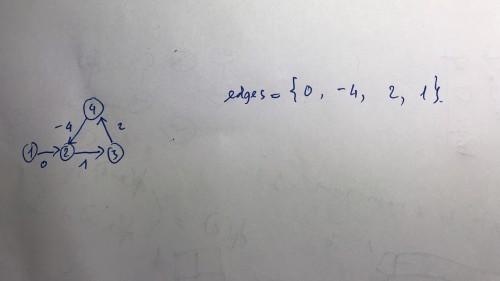I was gotten verdict wrong answer expected YES, found NO [4968th token] but I can't seek to this token because the web just show limited token. I wonder if I can get full test case of a problem to debug myself and if yes, how? Thanks community!!
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
I struggle to understand the statement of this problem. Could you help me re-declare this statement, thanks a lot.
I'm solving this Vietnamese problem which ask to calculate sum of first $$$n$$$ Tribonacci Number.
Tribonacci Number:
Let $$$S_n$$$ is the sum of first $$$n$$$ Tribonacci.
.
How to calculate $$$S_n$$$ with time complexity less than linear.
I have searched for it and found out we can use matrix multiplication to solve it with $$$O(log\ n)$$$. But with Fibonacci, we can based on relation between $$$F_n$$$ and $$$S_n$$$, $$$S_n = F_{n+2} - 1$$$. This article.
Could you help me figure out the relation between $$$T_n$$$ and $$$S_n$$$ in Tribonacci Number.
Thanks for your reading.
I see many people write your own pow function with module like this:
int pow(int a, int b, int m){
int ans = 1;
while(b){
if (b&1) ans = (ans*a) % m;
b /= 2;
a = (a*a) % m;
}
return ans;
}
and my pow function:
int pow(int a, int b, int m){
int ans = 1;
while(b){
ans *= a;
b--;
}
return ans;
}
The complexity of solution 1 is $$$O(log(b))$$$ ans solution 2 (my solution) is $$$O(b)$$$. I would like to know if it's the main reason to do that because I feel the 2nd solution easier to grasp and in the small situation (ex: b < 100), the second one is also good enough? Does it have any other reason?
I have solved UVa-10499 Traffic.
The problem ask to find out all shortest path from vertex 1, if vertices are affected by negative cycle, it means the shortest path become undefined and we print ?. I solved it with Bellman-Ford algorithm and it passed but I feel my approach is incorrect and I found a counter-example.
My approach: In the nth-relaxation, if vertices are shorten, I assign shortest path to them equal $$$-\infty$$$.
for(auto e:edges){
int u, v, w; tie(u, v, w) = e;
if (d[u]+w < d[v]) {
d[v] = -INF;
}
}
My fully solution: https://ideone.com/TfuoGz
For example, I have this graph and edges are stored in this order, the weight of edges represent the edges.
and in the n-th relaxation, I am just able to assign $$$-\infty$$$ to vertex 3, but vertex 2 and 4 are also affected by negative cycle.
Does the system test is weak or I understand something wrong? Could you suggest me the approach to solve this kind of problems.
Thank you!
I want to practice on Dijikstra topic, and I would love to solve problems on Codeforces too. How can I search for problems relate Dijikstra Topic on Codeforces. Thank you!
I am trying to solve ABC Path problem on SPOJ. I don't know where i missed. Why SPOJ don't give me test cases which my code is wrong on. Could you help me figure out it.
My code
Idea:
$$$dp[i][j]$$$: The longest consecutive sequence when we start at character $$$(i,j)$$$.
I use DFS to compute dp table.
After that, I iterate all characters $$$c[i][j]$$$ in the matrix, if c[i][j]=='A', I take the answer ans = max(ans, dp[i][j]).
Thank you!!!
The problem VK2012 B — File List.
I solved it by using greedy, but this problem was tagged dp and the editorial instructed dp approach such that:
is [i] — can we cut the prefix of length i .
Initially, is [0] = 1, the remaining zeros.
Now iterate over i in ascending order and if is [i] = 1, try to make the transition to i + 1 .. i + 12
I still can't solve it by DP, could you give me a more detailed explanation to solve this problem using DP? Thanks in advance!
I see a lot of people handling nCk with module(1e9+7) like that?
vector<ll> inv(h+w+1);
vector<ll> fact(h+w+1);
vector<ll> fact_inv(h+w+1);
inv[1] = 1;
for(int i=2; i<h+w+1; i++){
inv[i] = MOD - (MOD/i) * inv[MOD%i] % MOD;
}
fact[0] = 1;
fact_inv[0] = 1;
for(int i=1; i<h+w+1; i++){
fact[i] = fact[i-1]*i % MOD;
fact_inv[i] = fact_inv[i-1]*inv[i] % MOD;
}
auto comb = [&](int n, int k){
if (n<0 || k<0) return 0LL;
if (n < k) return 0LL;
return fact[n]*fact_inv[n-k] % MOD * fact_inv[k] % MOD;
};
What I can infer is that inv[i] is 1/i. Now, i don't understand the way they calculate inv[i]? Let me a more detailed explanation about that. Thanks in advance!
Hi Codeforces Community, I have just solved this problem.
Link problems
Even though I solved it by myself, i still feel i'm missing anything, i feel uncomfortable.
The problem requires we find out k ranges (size = m) in the way that sum of all elements in every ranges is maximal. I came up with the ideal that:
$$$f(i,j)$$$ is the maximum sum of all elements in j range (size = m) when we have already gone to a[i]. So
The answer will be $$$f(n,k)$$$.
I still feel like i don't understand it absolutely. As usual, i try to form my DP problem to a graph and find the shortest (or longest) path depended on statement.
I want to ask the way you approach for a DP problem.
Thanks in advance, i am studying dynamic programming.
I read many people's solutions and I realized the technique that helps me count effectively. This technique is:
If i want to increase all elements in range $$$[l;r]$$$ in array $$$cnt[]$$$, i will set $$$cnt[l]++$$$ and $$$cnt[r+1]--$$$, after that i will calculate cumulative sum from left to right, $$$cnt[i]+= cnt[i-1], \forall i \in [1:n]$$$.
The same approach is applied for 2d counting arrray. If i want to increase every cell in rectangle with top-left $$$(x_1, y_1)$$$ and bottom-right $$$(x_2, y_2)$$$. I will set cnt[x1][y1]++; cnt[x1][y2+1]--; cnt[x2+1][y1]--; cnt[x2+1][y2+1]++; and then calculate the partial sum of this 2d counting array.
I want to get more information for this technique. Could you help me the name of it or any link that is relevant. Thanks in advance.
This is the link of problem: D. White Line.
For the best i understand up to now, let's focus on row.
I will base on the range [l;r] each row of black to determine whether which cells that we click will erase this row or not. These cells are in the rectangle from $$$(l1, l2)$$$ (top left) to $$$(r1-1, r2-1)$$$ (bottom right), $$$l1, l2, r1, r2$$$ is defined in the code i extracted from @kcm1770's solution.
for(int i=0; i<n; ++i) {
int l=0;
while(l<n&&s[i][l]=='W')
++l;
if(l>=n) {
++b[0][0];
continue;
}
int r=n-1;
while(~r&&s[i][r]=='W')
--r;
if(r-l+1>k)
continue;
//i-k+1, i
//r-k+1, l
int l1=max(i-k+1, 0), r1=i+1;
int l2=max(r-k+1, 0), r2=l+1;
++b[l1][l2];
--b[l1][r2];
--b[r1][l2];
++b[r1][r2];
}
I see a lot of people do the same approach. I don't know how they come up with the way set ++ & -- like that. This is all of magic for me. Could you tell me about some similar problems using that or some concepts involve.
I have recently learn about Kruskals' Algorithm to solve Minimum Spanning Tree. I click problems under the tutorial and that leads me to 2500 tag problem. I tend to solve it but after seeing *2500 tag, i lose all of my confident =)). Lmao!!! Could you give me some advice. Thanks in advance.
I have read editorial all day but i can't figure out how it works. Could you give me a understandable explanation for this problem. Thanks in advance.
The problem link: https://csacademy.com/contest/archive/task/binary-flips/statement/
The Editorial link: https://csacademy.com/contest/archive/task/binary-flips/solution/
For me, i read editorial and think:
D(N,K,P) is the number of ways flips K times to construct a matrix with P columns all 1.
and when we discover $$$i\ col (all 1) * N + j\ row (all 1) * M - 2ij$$$ equals to S, we add D(N,K,i)* D(M,K,j) but i am pretty confused that: What guarantee K operations that construct i col 1 also construct j row 1. What wrong with my understand?
I have read Editorial and Code Example but I still don't understand the solution. Could you help me to explain more details. Thanks in advanced.
Link problem: https://csacademy.com/contest/archive/task/array-elimination/
| Name |
|---|