The answer for the problem is calculated with a formula ((a - 1 + b) 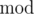 n + n)
n + n) 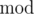 n + 1.
n + 1.
Such solution has complexity O(1).
There is also a solution with iterations, modelling every of |b|'s Vasya's moves by one entrance one by one in desired direction, allowed to pass all the tests.
This solution's complexity is O(|b|).
Let's consider the participants from every region separately. So for every region we just need to sort all of its participants by their score in non-increasing order. The answer for a region is inconsistent if and only if the score of the second and the third participant in this order are equal, otherwise the answer is the first and the second participant in this order.
The solution complexity is 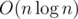 .
.
Our task is to take largest amount of toys Tanya doesn't have yet the way the sum of their costs doesn't exceed m. To do that one can perform greedy algorithm: let's buy the cheepest toy Tanya doesn't have at every step, while the amount of money left are sufficient to do that. The boolean array used can be a handle in that, storing true values in indices equal to toy types which Tanya does have at the moment. As soon as 109 money is sufficient to buy no more than 105 toys 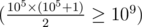 , used is enough to be sized 2 × 105 (we won't buy the toys with types numbered greater). So we just need to iterate over the number of type we want to buy, and if corresponding value in used is equal to false, we should buy it, otherwise we can't.
, used is enough to be sized 2 × 105 (we won't buy the toys with types numbered greater). So we just need to iterate over the number of type we want to buy, and if corresponding value in used is equal to false, we should buy it, otherwise we can't.
The solution complexity is 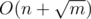 .
.
One can use the <> data structure (C++ \texttt{std::set}, for example), for storing the types Tanya has at the moment. In this case the complexity is 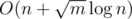 .
.
From the track description follows that Maria moves the way that the water always located to the right from her, so she could fall into the water only while turning left. To check if the turn is to the left, let's give every Maria's moves directions a number: moving to the north — 0, moving to the west — 1, to the south — 2 and to the east — 3. Then the turn is to the left if and only if the number of direction after performing a turn dir is equal to the number before performing a turn oldDir plus one modulo 4 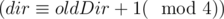 .
.
This solution has complexity O(n).
One can solve this problem in alternative way. Let the answer be equal to x (that means that the number of inner corners of 270 degrees equals x, but the number of inner corners of 90 degrees to n - x). As soon as the sum of the inner corners' values of polygon of n vertices is equal to 180 × (n - 2), then x × 270 + (n - x) × 90 equals to 180 × (n - 2). This leads us to 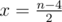 , being the answer for the problem calculated in O(1).
, being the answer for the problem calculated in O(1).
One should notice, that for every connected component of the graph the problem could be solved independently, so we just need to solve the problem for any connected graph.
Let this connected graph (of n vertices) contain n - 1 edge (such is called a tree). If one maintain a DFS from any of its vertex, every edge will be oriented, and each of them could given to its ending vertex, this way every vertex (except the one we launched DFS from, that is the root) will be satisfied by an edge. In this case the answer is equal to 1.
Let's then deal with a case when the graph contains more than n - 1 edges. This graph contains at least one cycle. Let's take arbitrary vertex from any of the cycles and launch a DFS (as above) from it. All vertices except chosen will be satisfied, so we are to give an edge to the chosen vertex. As soon as chosen vertex belongs to a cycle, at least one of its edge will not be taken to account in the DFS, so it can be given to a root. This way all the vertices will be satisfied.
Now we are able to solve the task for any connected graph, so we are to divide the graph into a connected components — this can be easily done by DFS or BFS.
The solution complexity is O(n + m).
In this task one should find a connected area, in which the product of the minimum value of the cells and the number of the cells is equal to k. To find such, let's sort all the n × m cells by their values by non-increasing order. Then we will consecutively add them in this order one by one, maintaining a connected components on their neighbouring relations graph. It's enough to use Disjoint Set Union structure to do so, storing additionally size of every component.
Let ai, j be the last added element in some component id, so ai, j has the minimum value among all the cells in component id (according to our ordering). If ai, j does not divide k, then the component id could not consist of desired area. Otherwise (ai, j is divisor of k), let's find need = k / ai, j — desired area size (if it contains ai, j), and if CNTid is not less than need, then the component id contains desired area, which could be easily found by launching a DFS in a neighbouring relation graph from ai, j, visiting only the ap, q ≥ ai, j and exactly need of them.
The solution complexity is 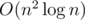 .
.
Let the answer for the problem be the sum

where calc(l, r) is the number of ways to cut the top part of the fence the way its leftmost part is in position l and the rightmost in position r. If l = r, that is the case when the cutted top part consists of part of only one board, then calc(l, r) = hl - 1.
Let r > l, then
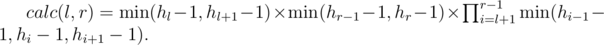
In other words, the number of ways to cut the top part of some board is equal to minimum value among heights of it and its neighbours minus one, otherwise the cutted part will be inconsistent. Leftmost board and rightmost board are considered separately, because each of them does have only one neighbouring board. So the answer looks like
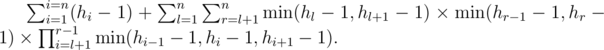
The first summand is easy to calculate, so let's take a look at the second. Let us modify it as the following:
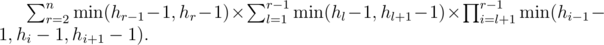
Let
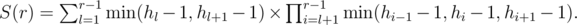
Let's take a look how does the S(r) change after increasing r by one:
S(r + 1) = S(r) × min(hr - 1 - 1, hr - 1, hr + 1 - 1) + min(hr - 1, hr + 1 - 1).
This way this sum is easy to maintain if consecutively increase r from 2 to n.
The solution complexity is O(n).










