Am I the only one seeing this?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |

Am I the only one seeing this?
Again, Im writing this both to help others and test myself so I will try to explain everything at a basic level. Any feedback is appreciated.
Disjoint Set(DS) data structures are representations of sets (which are all disjoint, sharing no elements) with certain functions:
FindSet(x): finds the set of element x
UniteSets(x,y): unites the sets x and y
MakeSet(x): makes a set with element x
Disunion(list): removes all elements from other sets and makes a new set with these elements
(Note: the disunion operation is not as commonly used as the other operations and is not implemented efficiently, with an O(n) runtime.)
DS is used in various algorithms, such as Kruskal's minimum spanning tree finder.
This post will proceed with a naive implementation, and then progress to an efficient solution.
We construct a forest (group of disjoint trees). Each element has a parent node and a list of children. (The list of children can be omitted if we are not intending to disunite sets.)
Define P(x): a function which maps an element to its "parent" element. In each set there will be exactly one parent, and P(parent) = parent, this is how a set is referred to.
Each element e starts as being in its own set, with P(e)=e. We can make an element easily with this element, and we can unite two sets X,Y with the following method.
Given two elements x,y, iterate P on each until P(x)=x, P(y)=y. Then set P(x)=y and add x to y's children. Now all elements that were children of x are children of y, so we have successfully united the two sets.
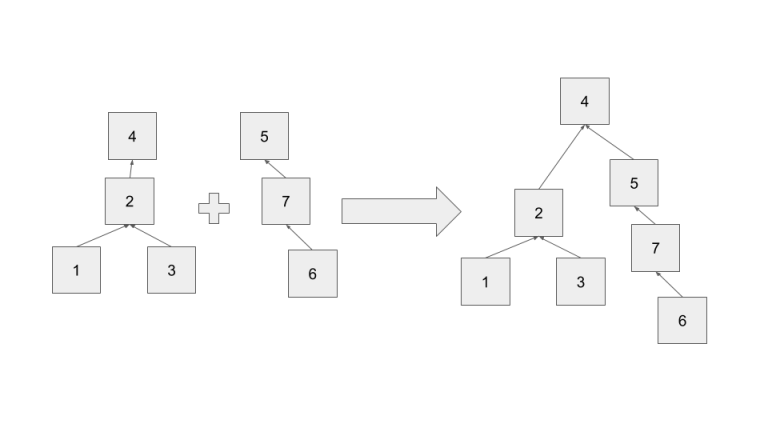
To disunite two sets, iterate through every node N (from farthest from root to root) that we are intending to breakaway. Change P of N's children to P(N) unless N=P(N) and N has more than one child or P(N) is going to be removed as well. If N=P(N)& N has more than one child (if it had one it could be removed with no consequence) instead make one of P(N)'s children the root. (Make sure not to select a child that is going to be removed, if all children are going to be removed go one level deeper.) If P(N) is going to be moved, repeat the procedure for P(N), with all of N's children included under P(N). As every node is processed at most once, the runtime is O(N(cost of removing from children + cost of adding to children)+(cost of building the new set, or n^2)).
Lets look at their runtimes:
FindSet : O(n), as in worst case the structure is a linked list.
UniteSets: O(n), as its runtime is determined by two FindSet calls.
MakeSet: O(1).
Disunion: O(n(cost of removing from children + cost of adding to children)+ n^2). Don't get too caught up memorizing the above algorithm, it is unwieldy and slow compared to the actual solution.
Looking at the first version of our DS one possible optimization becomes appearant. Our DS is a forest, so if all the trees were balanced, with a height of log N (something like a binary tree) then both FindSet and, as a result, UniteSets, will take O(log N) time.
As we build our sets from singular elements, our tree structure is determined by UniteSets. This points to potentially editing UniteSets to improve our runtime. Instead of arbitarily combining two sets, we can be smarter. Notice the height of the resulting tree is max(height(x)+1,height(y)) as height(x) and height(y)-1 are the heights of the two subtrees of root y after unification. Looking at this equation we notice some inefficency, if height(x)>height(y) then the height of the resulting tree is greater than if x became the new root. Thus, if we choose the taller tree's root as the final root, we have a more efficent solution.
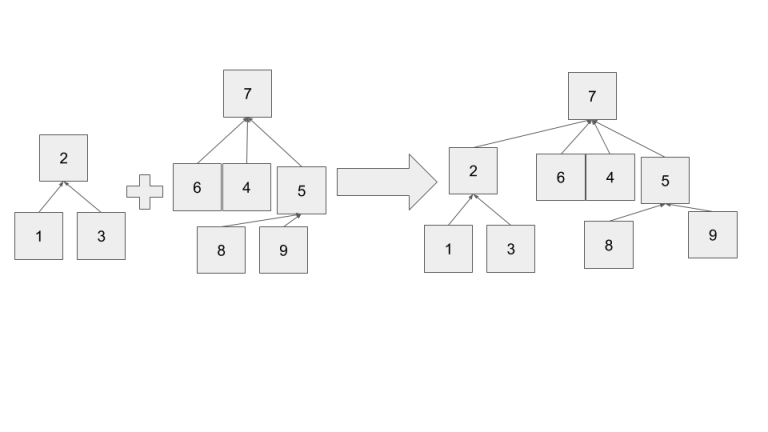
It turns out that this makes the tree's have a height of O(log N). Let the current maximum height of the whole DS be h. To increase h, we need to combine a tree with height h with another tree of height h (otherwise the max height wouldn't change.) Thus, a tree of height h+1 requires the sum of the elements in the trees of height h. Thus we get a recurrence, # of nodes in tree of height h+1 = 2*# of nodes in tree of height h. As it takes 2^n nodes to form a tree of height n, the height of a tree with N nodes is log N.
Lets look at the updated runtimes:
FindSet : O(log n), as in worst case the structure is a binary tree.
UniteSets: O(log n), as its runtime is determined by two FindSet calls.
MakeSet: O(1).
Disunion: O(n(cost of removing from children + cost of adding to children)).
The runtimes with optimization 1 are pretty good (Disunion will always be O(n) at worst as removing n arbitrary nodes requires touching all n nodes), but can we make them better? With path compression, we can make them even faster (and decrease the memory needed.) However, this heuristic makes analyzing the runtimes kind of complicated based on what you are using the DS for.
The inspiration for this optimization comes from inefficency in FindSet, namely that calling FindSet(x) with the same x multiple times still requires iterating up the tree. This inspires a dp solution, where we memoize the final parent of x. Then, realize that we kind of already do that with P. Instead of creating a seperate array, we can just update P.
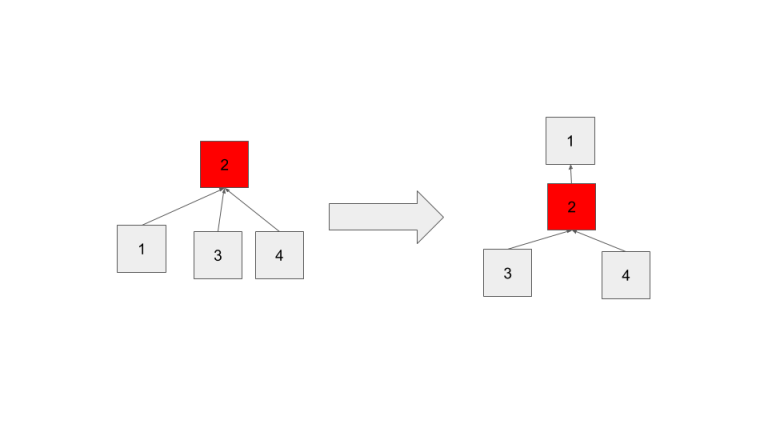
When we do path compression we do just that, for every node n from x to the root, set P(n)=root. That way, each of the nodes on the root are only 1 step from finding their parent. For these nodes FindSet becomes O(1).
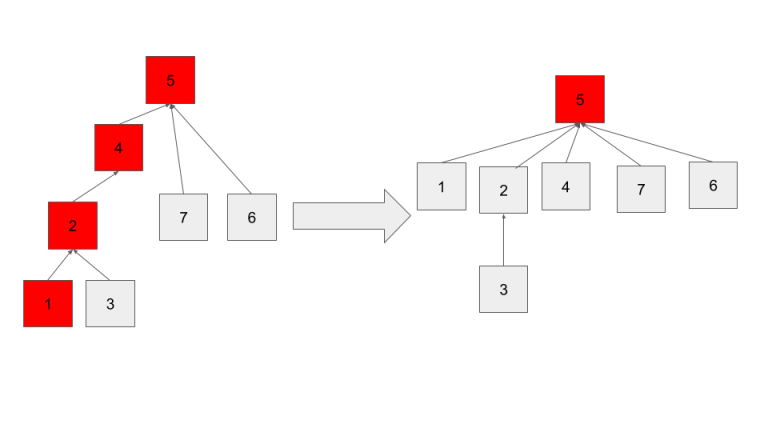
The above image shows path compression after calling findSet(1).
When we unite this set with other sets the distance from these nodes to their root could increase again, and thus our O(1) time progressively becomes ruined. Regardless, allowing path compression results in a much flatter tree, and thus on average reduces the runtime.
Note that with path compression, we can improve our disunion algorithm. We no longer need to store the children of each node. To disunion, run FindSet on every node in order to compress every node. This makes every tree have a height of two. Removing most nodes is now trivial, as they are leaves. Removing the roots is a little harder, but this can be accomplished intelligently. After compressing all the nodes, we again look at every node, and if a we process a node that is not a root whose parent is being disunioned and a root, instead make the non-root node the new root. Then, all the trees have a root that is not being removed (unless the whole tree is being removed, in which case we don't have to worry about it). After compressing all the nodes again, all disunioned nodes can be removed trivially and heights can be recalculated.
Lets look at our final runtimes:
FindSet : O(α(n)) (This and UniteSets' worst case is the reverse Ackermann function, as uniting two sets with path compression shortens the trees every union. This is effectively constant.)
UniteSets: O(α(n))
MakeSet: O(1).
Disunion: O(n).
All with O(n) space!
This implementation (especially disunion) isn't the most efficient/consise as readability has been emphasized. Also note that MakeSet has not been included as it doesn't even require a method proper, just setting par[x]=x. All the methods function as described above. par[x]= parent of x, rnk[x] = height of x (aka rank of x, notice that by default a set of height h has a rnk of h-1). Disunion functions by removing all elements with rm[x]=1, and setting their par to nroot.
#include <bits/stdc++.h>
#define MAXN 100000
using namespace std;
int par[MAXN],rnk[MAXN],N;
bool rm[MAXN];
int getPar(int x){
if(par[x]==x)return x;
par[x]=getPar(par[x]);
return par[x];
}
int unitePar(int x,int y){
int p1=getPar(x),p2=getPar(y);
if(rnk[p1]>rnk[p2]){
par[p2]=p1;
rnk[p1]=rnk[p2]+1;
}
else{
par[p1]=p2;
rnk[p2]=max(rnk[p2],rnk[p1]+1);
}
}
void disunion(int nroot){
int p;
for(int i=0;i<N;++i)getPar(i);
for(int i=0;i<N;++i){
p=getPar(i);
if(rm[p]&&!rm[i]){
par[p]=i;
par[i]=i;
}
}
for(int i=0;i<N;++i)getPar(i);
for(int i=0;i<N;++i){
if(rm[i]){
par[i]=nroot;
rm[i]=0;
}
}
memset(rnk,0,sizeof(rnk));
for(int i=0;i<N;++i){
p=getPar(i);
if(p!=i)rnk[p]=1;
}
}
Edit: fixed the final runtimes of findset and unitesets, thanks to farmersrice for pointing this out
Im writing this both to help others and test myself so I will try to explain everything at a basic level. Any feedback is appreciated.
A Fenwick Tree (a.k.a. Binary Indexed Tree, or BIT) is a fairly common data structure. BITs are used to efficiently answer certain types of range queries, on ranges from a root to some distant node. They also allow quick updates on individual data points.
An example of a range query would be this: "What is the sum of the numbers indexed from [1,x]?"
An example of an update would be this: "Increase the number indexed by x by v."
A BIT can perform both of these operations in O(log N) time, and takes O(N) memory.
(least significant bit will be abbreviated to LSB and in this post means the bit with the first one in the binary representation. Length of an interval ending at index x is shown by len(x))
BITs take advantage of the fact that ranges can be broken down into other ranges, and combined quickly. Adding the numbers 1 through 4 to the numbers 5 through 8 is the same as adding the numbers 1 through 8. Basically, if we can precalculate the range query for a certain subset of ranges, we can quickly combine them to answer any [1,x] range query.
The binary number system helps us here. Every number N can be represented in log N digits in binary. We can use these digits to construct a tree like so:
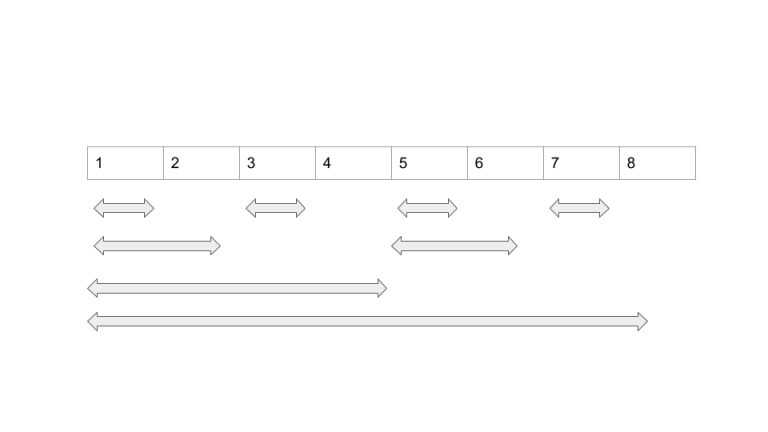
The length of an interval that ends at index I is the same as the LSB of that number in binary. (We exclude zero as its binary representation doesn't have any ones.) For example, interval ending at 7 (111) has a length of one, 4 (100) has a length of four, six (110) has a length of 2.
This gives the tree some interesting properties which make log N querying and updating possible.
A range query can be defined recursively [1,x] = [1,a-1] + [a,x] where [a,x] is the interval ending at x. x's which are powers of two are base cases as they contain the range [1,x] precalced. a is never below 1 as it is defined as the least sig bit in x, and x-LSB is either positive or a base case.
let len(index) = length of the interval ending at index.
We use the above recursion [1,x] = [1,a-1] + [a,x]. as len(x) = LSB in x, and a-1 = x - len(x), the least significant bit in a-1 is greater than len(x) (unless x is a power of two, in which case it is only one interval). (Subtracting len(x) from x removes this bit.) Since len(a-1) > len(x), len(a-1) >= 2 * len(x). This means that we approach 1 at an exponential rate, so it takes log N intervals to construct [1,x].
(Note that visualizing x as a binary integer, and recognizing that at each step in the recursion the LSB is turned to zero, and that we end when x reaches 0, means that it takes n steps (where n is the number of bits) at most, and these n bits represent 2^n numbers, so we can reach the logarithmic number of intervals this way too.)
This is essential to proving that updating takes log N operations.
Looking at the pictures this seems true, lets proceed with a proof by contradiction.
Assume intervals ending at a and b with len(a)=len(b) intersect, and without loss of generality let b>a. If these intersect, that means b-len(b)<a. Note that - len(b) is just removing the least sig bit. As len(a) = len(b) both a and b are indentical from the least sig bit to their start. This also means that as b > a, the binary number above these digits for b is greater than a. Removing the least sig bit from b doesn't change b>a as, in binary, the greater number is determined by the leftmost digit, as every digit carries more weight than all the previous digits combined.
Basically: b = [B]10...00 and a=[A]10...00 with [B]>[A]. b-len(b) = [B]00...00 which is still greater than a, so b cannot intersect a.
As there are a log N number of interval lengths, and no two lengths of the same size intersect, this means that any index is covered by at most log N intervals. Thus, updating an index requires updates to at most log N intervals.
In the above proofs we have found the method for querying efficently, but we still don't know how to update the nodes.
First note that as our ranges are defined by their rightmost endpoint, the range ending at x is the first range that contains x. So we need an algorithm that can quickly find the next largest range that contains x, and repeat until there are no more such ranges. The next range that contains x must be larger than the current one, so we know the next range's lsb > lsb of x. It turns out that the function next range = x + len(x) works. This is because this function increments the lsb to the next valid one.
Some people might notice a slight problem here, if we have a number like 111000, adding 1000 to that number gets 1000000, skipping a bunch of possible ranges. This is fine as the ranges that are skipped do not cover x. Trying to include the skipped ranges by removing ones just gets numbers that are lower than x, e.g. 110000<111000. Adding numbers to the end before increasing the lsb also doesn't work, as this moves the range ending further than the lsb increase does, e.g. 1110000 ends at 1100000 which is > 111000. The only way to increment to the next largest valid range is with x+=len(x).
Here is the procedure for updating a node x: update BIT[x], then add len(x) to x, repeat until x exceeds the size of the tree.
As every index only has one interval ending in it, it is possible to represent the BIT as an array. BIT[i] = the value of the interval ending at i.
Both update and query rely on getting len(x), or the lsb of x, easily. Thankfully, the bit operation (x&-x) returns the lsb.
Here's why:
let a=[A]10...00, then (thanks to 2-complements) -a = [A inverted]01...11 + 1 or [A inverted]10...00. Bitwise ANDing the two gets 000010...000, or the lsb of a.
Here is the actual implementation, using sum as the range query. (Note that we increment x so our tree is rooted at 1, as rooting at 0 causes problems.
int BIT[MAXN];void update(int x,int val) { ++x; while(x<=N) { BIT[x]+=val x+=(x&-x); } }
int query(int x) { ++x; int res=0; while(x>0) { res+=BIT[x]; x-=(x&-x); } return res; }
(I can't for the life of me figure out why the code isn't formatting properly... sorry.)(A little interesting fact is that x&=(x-1) functions the same as x-=(x&-x))
Thats it! Note that you can query for ranges [a,b] by performing query(b)-query(a-1). The same code can also be adapted to other range queries, but there are some pitfalls to look out for. Updating min and max doesn't always work, as you need to know the values in the range which you are updating, unlike in sum where all you need to know is the range's sum. For the same reasons you cannot query arbitary ranges [a,b] with the like you can with sums.
As a little aside, BITs are like a lightweight form of a segment tree. They take up less space (by a constant factor) and are quicker to code, but they are not as versatile as segment trees.
Again, this is my first time blog so any feedback is appreciated.
| Name |
|---|


