895A - Pizza Separation
We can notice that if one of the sectors is continuous then all the remaining pieces also form a continuous sector.If angle of the first sector is equal to x then difference between angles of first and second sectors is |x - (360 - x)| = |2 * x - 360| = 2 * |x - 180|. So for each possible continuous sector we can count it's angle and update answer.
Time complexity O(n2) or O(n).
895B - XK Segments
First, we need to understand how to find the number of integers in [l, r] segment which are divisible by x. It is r / x–(l - 1) / x. After that we should sort array in ascending order. For each left boundary of the segment l = a[i] we need to find minimal and maximal index of good right boundaries. All right boundaries r = a[j] should satisfy the following condition a[j] / x–(a[i] - 1) / x = k. We already know (a[i] - 1) / x, a[j] / x is increasing while a[j] increases. So we can do binary search on sorted array to find minimal/maximal index of good right boundaries and that mean we can find the number of good right boundaries.
Time complexity O(n * log(n)).
895C - Square Subsets
We can notice that x is a perfect square of some integer if and only if each prime number enters decomposition of x into prime factors even times. There are only 19 prime numbers less than 70. Now we should find the bitmask for each integer in [1, 70] by the following way: There is 1 in bit representation of mask in k-th place if k-th prime number enters decomposition of that number odd times. Else there is 0. For each integer between 1 and 70 we need to find the number of ways we can take odd and even amount of it from a. Let f1[i], f0[i] be that number of ways relatively. Let dp[i][j] be the number of ways to choose some elements which are <= i from a, and their product has only those prime numbers in odd degree on whose index number j has 1 in binary representation. Initially dp[0][0] = 1.
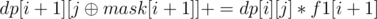
dp[i + 1][j] + = dp[i][j] * f0[i + 1]
The answer is dp[70][0].
Time complexity is O(max*2^cnt(max)), where max is maximal integer a[i], and cnt(max) is the number of prime numbers less than max.
895D - String Mark
Suppose that we can calculate the function f(s) equal to the number of permutations of the string a strictly less than s. Then the answer is f(b) - f(a) - 1. Now we need to understand how to find f(s). First we should count the number of occurrences of each letter in the string a, cnt[26].Than we can iterate through the position of the first different symbol in the permutation a and the string s and update the number of remaining symbols cnt[26]. For each such position, we need to iterate through the symbol in the permutation of a which will stand in this position. It must be less than the character at this position in the s string. For each such situation we can calculate and add to the answer the number of different permutations that can be obtained using symbols not currently involved. Their number is stored in cnt[26]. In its simplest form, this solution works in O(n * k2), where k is the size of the alphabet. Such a solution can't pass the tests, but it can be optimized to O(n * k), and that is enough to solve the problem.
Time complexity O(n * k), where k is the size of alphabet.
895E - Eyes Closed
For each position we need to maintain mathematical expectation of the value on it. Initially, for position i, it is a[i]. Let's process the query of the first type. Each number from the interval [l1, r1] remains on its place with probability (r1 - l1) / (r1 - l1 + 1). The probability that it will be replaced by a number from [l2, r2] is 1 / (r1 - l1 + 1). The mathematical expectation of the number to which it will be replaced is the arithmetic mean of sum of the mathematical expectation of numbers in [l2, r2], let it be x. Then, to update the expectation of a number from [l1, r1], we need to multiply it by (r1 - l1) / (r1 - l1 + 1) and add x / (r1 - l1 + 1) to it. That is, the query of the first type is reduced to the query multiplying all the numbers in a segment and adding to them a number. To process the second type query, you must find the sum of the numbers in the segment. All these queries can be processed with the help of segment tree.
Time complexity O(x + q * log(n))









