Given the side length of one equilateral triangle and 3 radii R1, R2, R3 which produce 3 sectors inside the triangle. Calculate the area of the triangle which is not covered by the sectors.
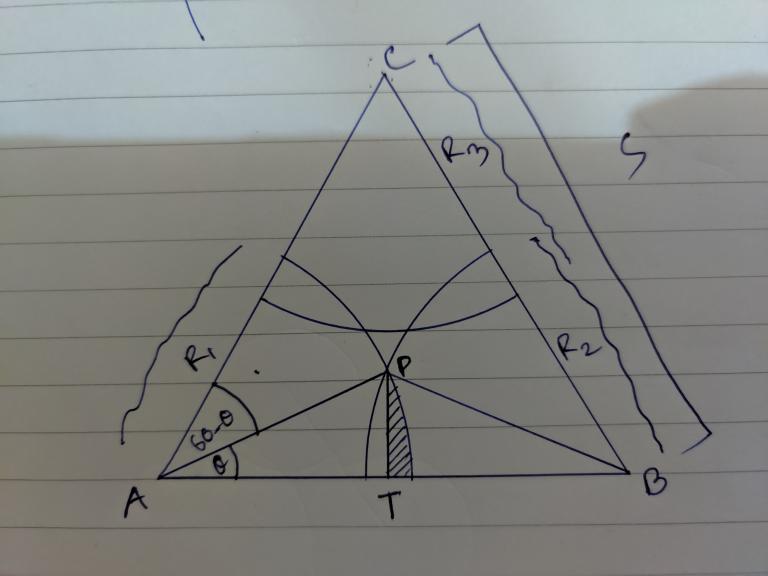
My idea is
We can see there can be three cases.
- any radius from R1, R2, R3 is greater than or equal to S for which the answer will be Zero
- if
R1+R2<S and R2+R3<S and R3+R1<Sso the answer will be Area of ABC — Area of 3 sectors - if one sector intersects with another...
For this case, I will check if every pair of circle intersects or not. For this let's denote P as the intersection point. and let's draw a line PT which is perpendicular to the line AB. so from triangle APT and the new sector with an angle60-Thetaso I can get the dashed area from Previous sector Area — (new sector area + triangle APT). with same this approach, I can get the opposite dashed area too which is calculated twice in the addition of sectors area since they intersect. So I'll subtract it from the original sector area.
I'm getting WA with this approach. can you please help me find my mistake :) I'll be glad.
My solution
Problem Link (Problem J)
you can submit your solution for this problem here to check if it gets AC Judge










