Hi codeforces!
Quick Sort is a sorting algorithm (duh).
History:
A bit about its history, It was developed by a British computer scientist Tony Hoare (Not that it helps in understanding the algorithm)
Application / Where to use Quick Sort:
There are many sorting algorithms then why do we need to learn/ use quick-sort? Quick sort is used in places where we need to efficiently sort the elements. It is also used when there are restrictions in space availability.
What is the time complexity of quick sort:
Quick sort has an average time complexity of O(n log n) but if we don't chose the pivot correctly, the worst case time complexity is O(n^2).
How Quick Sort works:
Quick sort can be related in the real life like this. Suppose a student comes to a teacher and asks her to tell the student s who are better than him and the ones who are weaker than him. Now the teacher looks at the class in the order they are sitting, and for each student tells whether that student is stronger or weaker. As the students may not be sitting in the right order, we only get a relative comparison and we cannot sort the items. Quick sort makes use of this principle.
Now lets move to quick sort, in quick sort we chose an element as a pivot element which is similar to the person who came to the query in the above example. and we check for each element whether it is smaller or larger than the pivot one. if we find two such pairs of elements such that one lies to the left of the pivot and is still bigger than the pivot and one which lies in the right side of the pivot but is numerically smaller than the pivot, we swap those two elements.
Example:
I feel that this can be understood better with an example:
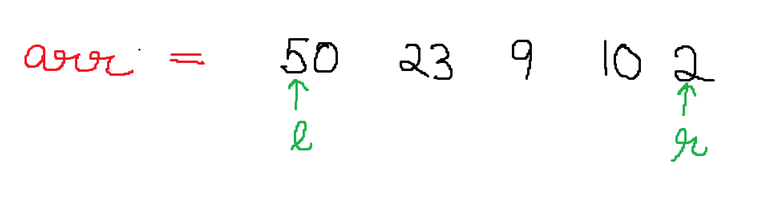
Now we chose a pivot element. Lets say we chose 9.Now we take 2 points one from index 0 and one form index n-1. Now we go increase the l till we reach an element which is more than the pivot. In our example we would not need to move as arr[0] itself is larger than the pivot.
Now we move r backwards until we get a element which is smaller than the pivot element. In our case we dont have to move as arr[n-1] is lesser than the pivot element. Once we have got this we swap the elements are l and r. After the first swap the array looks like this.
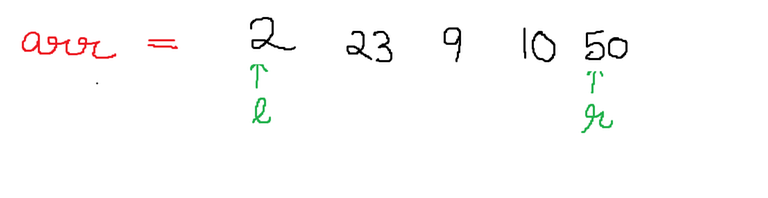
As we continue on the same pivot we realize that 23 and 9 are misplaced too and have to swapped. so after the second swap the array looks like:
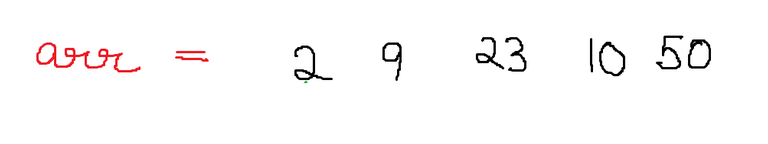 .
.
Now we partition the array into two smaller arrays.
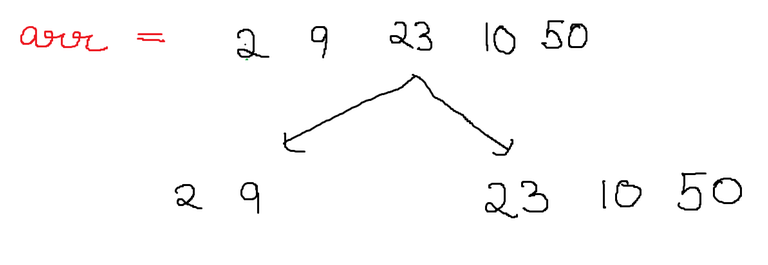
Now we can repeat the same operations on the smaller arrays. It is for this reason Quick sort is an example of Divide and Conquer Algorithm.
.
Code for QuickSort
#include<bits/stdc++.h>
using namespace std;
int partition(int arr[], int l, int r , int pivot){
while(l<=r){
while(arr[l]<pivot){
l++;
}
while(arr[r]>pivot){
r--;
}
if(l<=r){
swap(arr[l],arr[r]);
l++;
r--;
}
}
return l;
}
void quick_sort(int arr[], int l , int r){
if(l>=r){
return;
}
int pivot = arr[l+(r-l)/2];
int partition_index = partition(arr,l,r,pivot);
quick_sort(arr,0,partition_index-1);
quick_sort(arr,partition_index,r);
}
int main() {
int arr[5] = {50,23,9,10,2};
cout<<"Previously:"<<endl;
for(int i = 0;i<5;i++){
cout<<arr[i]<<" ";
}
cout<<endl;
quick_sort(arr,0,4);
cout<<"After Sorting"<<endl;
for(int i = 0;i<5;i++){
cout<<arr[i]<<" ";
}
return 0;
}
Space Complexity
Space Complexity of Quick sort
The space complexity is calculated based on the space used in the recursion stack. The worst case space used will be O(n) . The average case space used will be of the order O(log n). The worst case space complexity becomes O(n), when the algorithm encounters its worst case where for getting a sorted list, we need to make n recursive calls.
Hope you learnt something new or revised an old topic!
Now that you have made it this far here is a rainbow bunny for u!











