Problem analysis v 0.9.
In this problem we need to understand how exactly numbers from 1 to n rearrange when we write firstly all odd numbers and after them all even numbers. To find out which number stands at position k one needs to find the position where even numbers start and output either the position of the odd number from the first half of the sequence or for the even number from the second half of the sequence.
In the heavy metal problem one needs to find the number of the substrings in the string S with a given prefix A and given suffix B. If we mark black all the starting positions of the entries of the string A in S, and white all the starting positions of the entries of the string B, then we come to the following problem: count the number of pairs <black position, white position> (in this order). To solve this it is enough to iterate from left to right counting the number of the passed black positions. Meeting black position we increment this number by one, meeting white position we add to the answer the number of pairs with this white position, which is exactly our memorized number of the already passed black positions.
This problem were more about accuracy then about ideas or coding. It is important to not forget any cases here.
On each step we replace one of the numbers x, y by their sum x + y until the pair becomes m-perfect (id est one of them becomes not lesser than m). It is clear that one sould replace lesser number from the pair x, y. Indeed lets say the pair x1 ≤ y1 dominates the pair x2 ≤ y2, if y1 ≥ y2 and x1 ≥ y2. In this case if one can get m-perfect pair from x2, y2 by certain sequence of actions, then one can get m-perfect pair from x1, y1 by the same or shorter sequence of actions. If x ≤ y, then the pair x + y, y dominates the pair x + y, x. Hence path from x + y, y to m-perfect is not longer than from x + y, x, and we may assume that we choose exactly this pair.
Consider following cases:
x ≤ 0, y ≤ 0 In this case our numbers do not increase in the process. Hence either the pair is alredy m-perfect or it will never be.
x > 0 and y > 0 In this case for each m pair will after several steps become m-perfect. To count precise number of those steps one needs to launch emulation. If x > 0 and y > 0, then pair "grows exponentionaly>> (more formally: easy to show that starting from secnd step sum x + y grows in at least 3 / 2 times each step) and emulation works pretty fast. However in the case x < 0 and y > 0 (or vice versa) pair might change very slowly. Most bright example is x = - 1018, y = 1. Thus one needs to count number of steps until both numbers becomes positive before launching emulationt. For x < 0 and y > 0 number of those steps is exactly
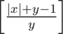 .
.
One may reformulate the problem ass follows. Non-negative integers A(x, y) are placed in the vertices of two-dimensional lattice 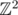 We may imagine this construction as a function
We may imagine this construction as a function 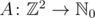 . On each step for each vertex P = (x, y) with A(x, y) ≥ 4 we perform operation φP, which substracts 4 from A(x, y) and adds 1 to A(x, y - 1), A(x, y + 1), A(x - 1, y), A(x + 1, y). We may think that operation φP applies to the whole function A. We need to find values of A after the iterations stops.
. On each step for each vertex P = (x, y) with A(x, y) ≥ 4 we perform operation φP, which substracts 4 from A(x, y) and adds 1 to A(x, y - 1), A(x, y + 1), A(x - 1, y), A(x + 1, y). We may think that operation φP applies to the whole function A. We need to find values of A after the iterations stops.
Key idea is that operactions φP and φQ for all points P and Q commutes, that is φP(φQ(A)) = φQ(φP(A)). This means that the order of operations is unimportant. In particular, we may assume that from each given vertex run all possible four-groups of ants and not only one. After this observation one may run full emulation of the process. As an exercise contestants may check that ants will never leave square 200 × 200 with center in the origin 0 with given constraints.
In this problem we need to find 2n2 transfusions from initial configuration to the desired one. First of all we propose the following: if in each connected component overall volume of the water in initial configuration is the same as in desired one, then answer exist. We call the vessel ready, if current volume of its water equals desired one. Let us describe solution which is probably easier to code. We will make vessels ready one by one. Consider the pair of non-ready vessels s and t (there is more water in s than desired, and less water in t than desired), such that they are connected by the path P, and if one transfuses d litres from s to t then one of the vessels becomes ready. Now we need to find a way to transfuse d litres by path P from s to t. One may write recursive function pour(s, t, d) for this aim. Let t' stand before t in this path, then function works as follows: transfuses from t' to t as many water as possible (not more than d of course), then calls pour(s, t', d) and on the final step transfuses from t' to t all that left. It is easy to check that all such transfusions are correct. This algorithm makes 2len transfusions on the path of length len, so total number of transfusions is not greater than 2n2.
For each numner x denote sequence of its powers within [1..n] as Pow(x): 
Game proceeds as follows: on each step one player takes still available number x from 1 to n and prohibits whole set Pow(x). Who can't make his turn loses.
This game may be decomposed in the sum of lesser games. Indeed, lets call number x simple (and corresponding sequence Pow(x) simple), if it is not a power of any number y < x. Then: 1. for each 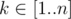 there is simple x, such that
there is simple x, such that 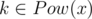 ; 2. for each simple distinct x and y sets Pow(x) and P(y) do not intersect. Indeed, for a given k there is exactly one simple x such that k is power of x. This may be showed from fundamental theorem of arithmetic: if
; 2. for each simple distinct x and y sets Pow(x) and P(y) do not intersect. Indeed, for a given k there is exactly one simple x such that k is power of x. This may be showed from fundamental theorem of arithmetic: if 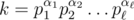 and d = gcd(α1, α2, ..., αn), then
and d = gcd(α1, α2, ..., αn), then 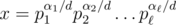 .
.
Hence set [1..n] decomposes into primitive sets Pow(x), on each of those Pow(x) game proceeds independetly. Now one may use Sprague–Grundy theory to see that mexx of our game is just xor of all mexx of games on simple Pow(x). For fixed x, if Pow(x) = {x, x2, ..., xs}, then mexx of the game on Pow(x) depends only on s, but not on x. In our case s runs from 1 to 29, mexx for all such s may be directly precalculated. Now it is enough to find numbers q(s) of simple x with a given size of Pow(x) equal to s (actually we are interested in parity of q(s) not in q(s) itself).
Our constraints allows to do it directly: run x from 2 to  , if it is not crossed out, determine the size Pow(x) [increment corresponding q(s)], and cross out all numbers from Pow(x).
, if it is not crossed out, determine the size Pow(x) [increment corresponding q(s)], and cross out all numbers from Pow(x).
This cycle finds all simple sequences of length at least 2. Quantity of non-crossed numbers is the number of all simple sequences of length 1. Now it is enough to look at parities of q(s) and xor coressponding mexx.
However one may find all q(s) for  . Indeed lets look at the number
. Indeed lets look at the number 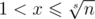 and sequence {x, x2, x3, x4, ..., xs}. This sequence is not simple iff it is containd in some larger simple sequence. But number of subsequenes of size s in a given sequence of size t > s is easy to find: it is just [t / s]. Recalling that simple sequences do not intersect one gets the reccurent formula:
and sequence {x, x2, x3, x4, ..., xs}. This sequence is not simple iff it is containd in some larger simple sequence. But number of subsequenes of size s in a given sequence of size t > s is easy to find: it is just [t / s]. Recalling that simple sequences do not intersect one gets the reccurent formula:
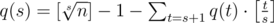 .
.
Now it is easy to find all q(s) from q(29) to q(1).
Remark: while coding it is important to remeber simple number x = 1.
317E - Princess and Her Shadow
In this problem princess Vlada should simply catch the Shadow. Here is the idea of a solution. If there is only one tree, then using it as a barrier to the shadow it is not hard to catch the shadow. Similar technique works if Vlada and Shadow are far from the square where all the trees grow. But what can she do in the dark depths of the forest? If there is no path at all between Vlada and Shadow, then there is no way to catch it. Otherwise consider a shortest path from Vlada to the Shadow and make Vlada follow it. This path gives Vlada a queue of the steps that she should perform. Additionaly if shadow moves, then we add her move to the queue (simply speaking Vlada follows the shadow). This is where the algorithmic part ends. Now we state that either Vlada catches the shadow in the desired number of steps, or steps out of the "forest square". To proof this we note that the length of the path between Vlada and Shadow may only decrease. And if it does not decrease long enough, then once in k steps (k is the length of the path) Vlada and Shadow shifts at the same vector over and over, and at some moment leaves the "forest square". Note that if the trees allow our heroes to step out of the "forest square" at the beginning, then we may just get them out from the start. But taking this approach we still need to catch the Shadow in a "labyrinth forest".
Apologies for the delay. There are probably misprints and mistakes here (thousands of them!), please feel free to point them out.










