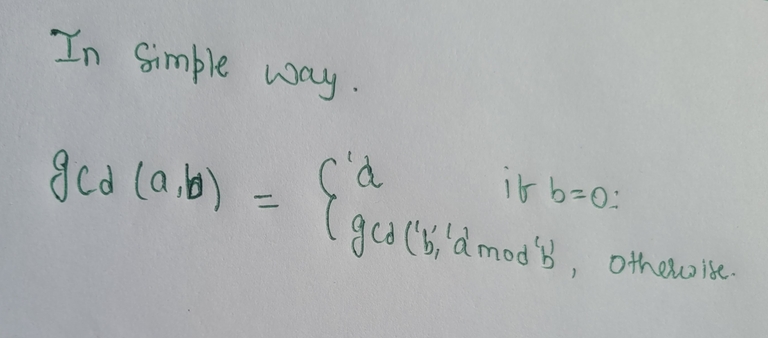Knapsack is a standard problem of dp (Dynamic programming) in which you need to pack a set of items, with given values and sizes (such as weights or volumes), into a container with a maximum capacity.

Identification

You have a container with a maximum capacity given. and given two arrays one array contains value and other containing weight/limits respectively. You have to find optimal value you can obtain within the bag's size limit. and we have a choice along arrays.

Knapsack can be divided into three sub problem.

1. Fractional Knapsack :- Easily solved using Greedy. In this problem you have given all thing that kanpsack have but you can use value in fraction means if you have given a weight $$$4kg$$$ with value of $$$10$$$ then we can use $$$1kg$$$ with a weight of $$$2.5$$$.

2. 0-1 Knapsack :- In this we can use one weight only one time also we can't break into pices. we have to use dp to find solution of this type of problem as we have a choice among array that we can choose it or not, so there must be overlapping subproblem so we have to store value that we had have already obtained.

3. Unbounded Knapsack:- In this type of problem we have no restriction on number of time a element, that means we can use a element any number of times to obtain it. But we can't break a piece into smaller pieces like in fractional knapsack. int this problem we have choice that we can choose a weight or not so this is also solved using DP.

0-1 Knapsack

Problem statment.

Given N items where each item has some weight and profit associated with it and also given a bag with capacity W,The task is to put the items into the bag such that the sum of profits associated with them is the maximum possible.

profit_array[]={1, 4, 2, 3, 5}, Weight_array[]={1, 8 , 5, 7, 9}, W(maximum capacity of bag)= 5.

Thinking process;

we can surely look that we have many choice in which we can get $$$5$$$ as weight like weight = $$$3+2$$$ in which we can get overall profit of $$$7+5$$$, if we choose $$$4+1$$$ we can get a value of $$$8+1$$$, like that.

we have to make choice on every element that we can choose it/pick it or not, here come the recursion in the figure in which we can write a code for a case then it will solve automatic.

we have two choice on every element that we can choose it or not.

Dry Run

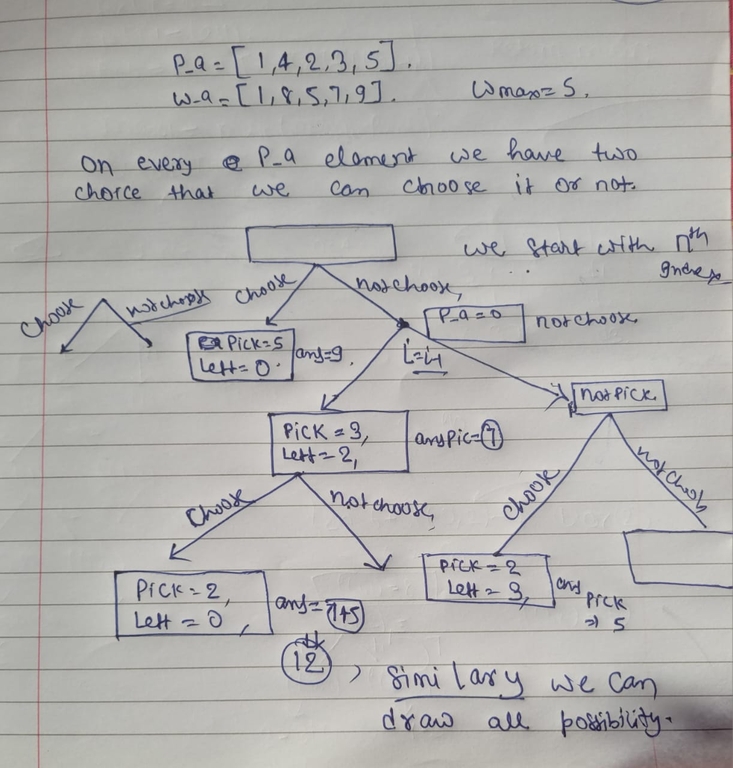
lets describe base case and some restricted area

1. We are starting from $$$n-1$$$ index then if reach at $$$0th$$$ index then we have to return it

2. In every case when we are going to choose an index then we have to check that the index we hve choosen its weight is less than or equal to weight avaliable in bag.

Code With recursion

int rec(vector<int> &Weight, vector<int> &value, int i, int w)
{
    if (i == 0)
    {
        if (Weight[0] <= w)
            return value[0];
        return 0;
    }
    int pick = INT_MIN;
    if (Weight[i] <= w) pick = value[i] + rec(Weight, value, i - 1, w - Weight[i], dp);
    int not_pick = rec(Weight_arr, value, i - 1, w, dp);
    return max(pick, not_pick);
}
int knapsack0_1 (vector<int> weight, vector<int> value, int n, int maxWeight)
{
    return fn(weight, value, n - 1, maxWeight);
}

Time Complexity: O(2N)

Here come the Dp in figure in which we solve overlapping problem only one time and store it in a matrix.

For this we have to make a matrix of which store value at parameter which is changing like in this problem changing parameter is $$$index$$$ and $$$maxWeight$$$ so we have to make 2-D vector of size [index+1][maxWeight+1] and give a value that will never come in figure and we can easily identify it that this index id solved or not, let initilize with $$$-1$$$,

And in code we have to solve when dp[index][maxWeight]==-1 otherwise we can return dp[index][maxWeight] because in recursion if we reach at a place then it dosen't matter that from where we come.

Code with DP (Memoization Approach)

int fn(vector<int> &Weight, vector<int> &value, int i, int w, vector<vector<int>> &dp)
{
    if (i == 0)
    {
        if (Weight[0] <= w)
            return val[0];
        return 0;
    }
    if (dp[i][w] != -1)return dp[i][w];
    int pick = INT_MIN;
    if (Weight[i] <= w)
        pick = value[i] + fn(Weight, value, i - 1, w - Weight[i], dp);
    int notpick = fn(Weight, value, i - 1, w, dp);
    return dp[i][w] = max(pick, notpick);
}
int knapsack0_1 (vector<int> weight, vector<int> value, int n, int maxWeight)
{
    vector<vector<int>> dp(n + 1, vector<int>(maxWeight + 1, -1));
    return fn(weight, value, n - 1, maxWeight, dp);
}

Time Complexity: O(N * W).

Auxiliary Space: O(N),Stack space required for recursion

Auxiliary Space: O(N * W) + O(N). The use of a 2D array data structure for storing intermediate states and O(N) auxiliary stack space(ASS) has been used for recursion stack

we have many similar problem related to 0-1_knapsack like

1. Subset sum Problem (problem)

2. Partition Equal Subset Sum (Problem)

3. Target sum (Problem)

4. Partition array into two arrays to minimize sum difference (Problem)

5. Count subset sum (Problem)

You can solve many problem D and E on (Atcode DP sheet)

1446A - Knapsack

Thanks.

GCD

• Gcd of two natural number $$$a$$$ and $$$b$$$ is defined as the largest number which is a divisor of both $$$a$$$ and $$$b$$$.

• Mathematically it is defined as: GCD(a, b)= max{k>0: (k/a) and (k/b)}.(Here $$$k$$$/$$$a$$$ means $$$k$$$ divides  $$$a$$$).

  Ways to find GCD

  Brute Force

• We can find gcd of two number by checking for all integer less than both number.

• We never use this approach to find gcd because this run in O(n) time complexity.

  Euclidean algorithm

• The Euclidean algorithm was formulated as follows: subtract the smaller number from the larger one until one of the numbers is zero. Indeed, if   $$$g$$$ divides   $$$a$$$ and   $$$b$$$, it also divides   $$$a-b$$$. On the other hand, if   $$$g$$$ divides   $$$a-b$$$ and   $$$b$$$, then it also divides   $$$a = b + (a-b)$$$, which means that the sets of the common divisors of   $$${a, b}$$$ and   $$${b,a-b}$$$ coincide.

• $$$a$$$ remains the larger number until   $$$b$$$ is subtracted from it at least   $$$\left\lfloor\frac{a}{b}\right\rfloor$$$ times. Therefore, to speed things up,   $$$a-b$$$ is substituted with $$$a-\left\lfloor\frac{a}{b}\right\rfloor b = a \bmod b$$$.

Implementation Using Code

1. Recursive Code

    int gcd (int a, int b) {
       if (b == 0)
        return a;
       else
     return gcd (b, a % b);
     }

This code run in O(log min(a, b)) Time complexity and in Recursive Stack space complexity.

2. Iterative Solution

    int gcd (int a, int b) {
      while (b) {
        a %= b;
        swap(a, b);
      }
      return a;
    }

This code run in O(log min(a, b)) Time complexity and But it take a constant space complexity as we have only define two variable only. This solution is is more faster than recursive one because of recursive call take more time than normal iteration.

Binary GCD

Above method works in time complexity of O(log n).we can more optimize this as we all know that The slow part of the normal algorithm are the modulo operations. Modulo operations, although we see them as   $$$O(1)$$$, are a lot slower than simpler operations like addition, subtraction or bitwise operations.. Here comes the Binary GCD in role.

This uses three very popular properties of GCD

• If both numbers are even, then we can factor out a two of both and compute the GCD of the remaining numbers:   $$$\gcd(2a, 2b) = 2 \gcd(a, b)$$$.
• If one of the numbers is even and the other one is odd, then we can remove the factor 2 from the even one:   $$$\gcd(2a, b) = \gcd(a, b)$$$ if   $$$b$$$ is odd.
• If both numbers are odd, then subtracting one number of the other one will not change the GCD:   $$$\gcd(a, b) = \gcd(b, a-b)$$$

Implementation Using Code

    int gcd(int a, int b) {
      if (!a || !b)
        return a | b;
      unsigned shift = __builtin_ctz(a | b);
      a >>= __builtin_ctz(a);
      do {
        b >>= __builtin_ctz(b);
        if (a > b)
            swap(a, b);
        b -= a;
      } while (b);
     return a << shift;
    }

Thanks.