Hello everyone,
in this blog I'm trying to convince you that editorials are useful, especially if you read them "correctly".
"Algorithm $$$1$$$" vs "Algorithm $$$2$$$"
This is what many users do when reading the editorial for one problem (let's call it "algorithm $$$1$$$"):
- Read it.
- Repeat until able to implement the solution.
- Implement the solution; possibly forget about any previous attempt to solve that problem without editorial, and any detail in the editorial that seems unrelated to the implementation of the solution.
- Possibly, read the comments trying to find out how it is possible to come up with the solution in the editorial.
This is what you should do in my opinion (let's call it "algorithm $$$2$$$"):
- Keep the editorial open until you are able to implement the solution, using both your ideas and editorial's ideas: sometimes, this just means opening the editorial for $$$1$$$ second, because you had already found most of the ideas on your own.
- Implement the solution.
- Re-read the editorial carefully, and pretend you can modify it; ask yourself which parts of the editorial you would modify.
- Possibly, read the comments to find additional insights / ideas.
(I'm not saying "algorithm $$$2$$$" is the best way to use editorials. It's just a method that works for me, and seems strictly better than "algorithm $$$1$$$". Feel free to find your own way to use editorials.)
Examples:
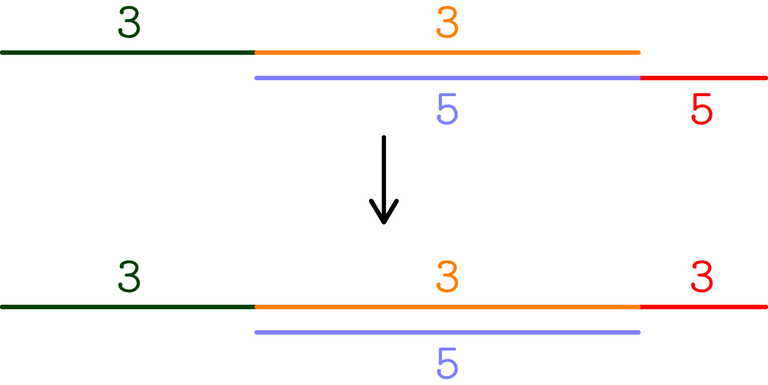
1909B - Make Almost Equal With Mod
Algorithm $$$1$$$:
- Read the editorial.
- Understand that, for some unintuitive reason (i.e., some math formulas), you only need to check $$$k = 2^i$$$.
- Implement the solution.
- Read the comments; find out that an alternative solution is printing $$$k = 2 \cdot \gcd(|a_i - a_{i+1}|)$$$. Convince yourself that you could come up with that by trial and error, and lots of small examples on paper (i.e., do some "proof by examples").
Algorithm $$$2$$$:
- Look at the picture for some time (between $$$1$$$ second and $$$5$$$ minutes), understand what's going on, understand the solution.
- Implement the solution.
- Re-read the editorial carefully. Read the comments and find out that an alternative solution is printing $$$k = 2 \cdot \gcd(|a_i - a_{i+1}|) =: 2g$$$. This seems a completely different solution, but let's check if you can use the editorial to prove it fast.
- We have to prove $$$f(2g) = 2$$$. But $$$f(g) = 1$$$ because all the $$$a_i$$$ modulo $$$g$$$ are the same. Then, either $$$f(2g) = 1$$$ or $$$f(2g) = 2$$$ (according to the editorial). But $$$f(2g) \neq 1$$$ because otherwise $$$\gcd(|a_i - a_{i+1}|)$$$ would be a multiple of $$$2g$$$.
With both algorithm $$$1$$$ and algorithm $$$2$$$ you would learn two solutions, but only with algorithm $$$2$$$ you would have a "full" understanding of them.
- With algorithm $$$1$$$, you could get conclusions such as "when number $$$2$$$ appears in the statement, consider binary representation" or "when $$$\text{mod}$$$ appears in the statement, consider $$$\text{gcd}$$$" which seem random and not so practical.
- With algorithm $$$2$$$, you have an intuitive visualization and an actual proof of the solution. You have also used the proof in the editorial to prove another (seemingly unrelated) solution (so proofs are not useless!). You learned the "binary" trick, but you also got better at proving stuff.
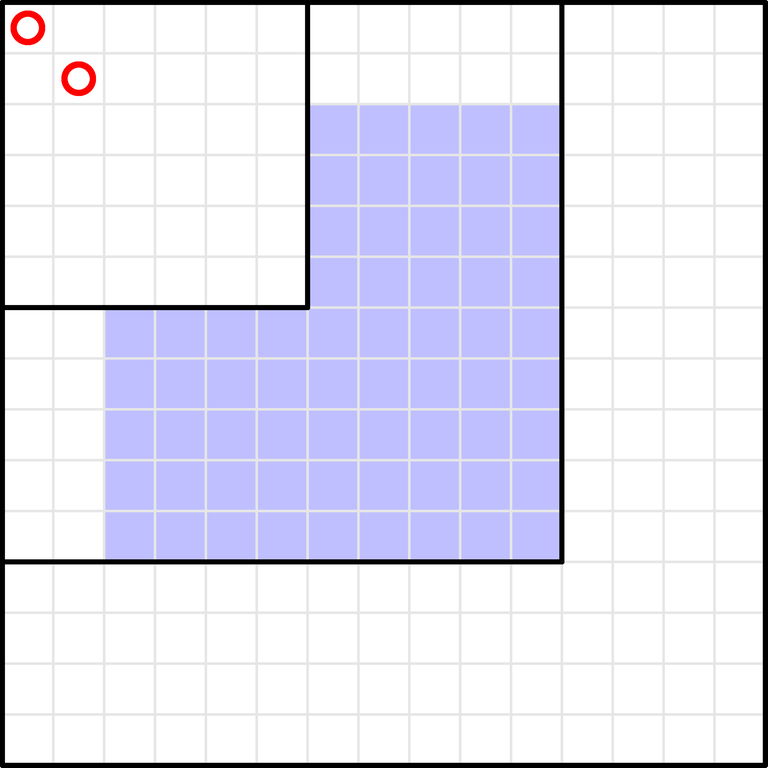
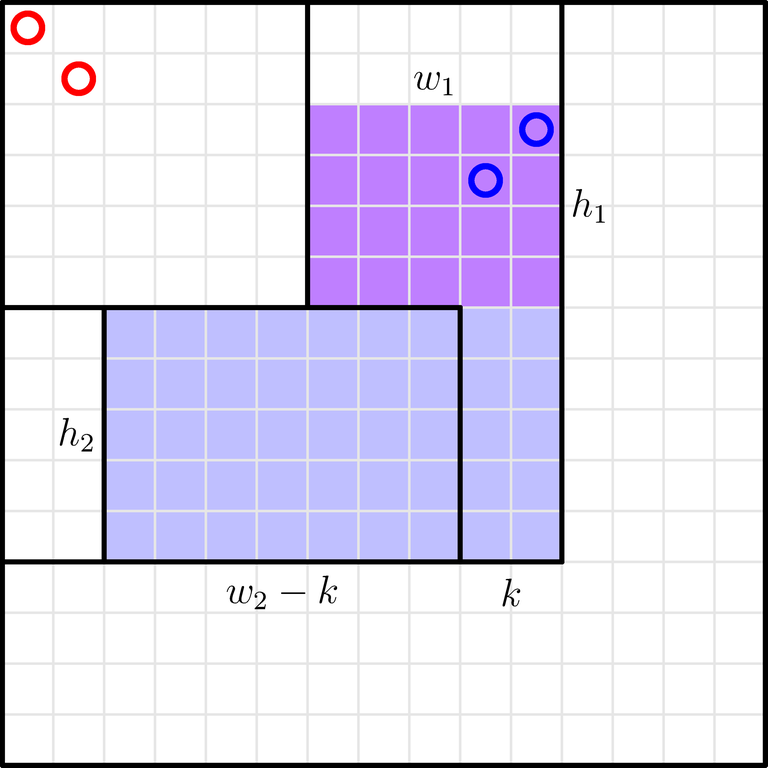
1909C - Heavy Intervals
Algorithm $$$1$$$:
- Read the editorial.
- Understand that, for some unintuitive reason (i.e., a proof which seems unnecessarily long), you need a bracket matching.
- Implement the solution.
- Read the comments; find out that many people tried to sort $$$l$$$ and $$$r$$$ in ascending order, but somehow it does not work.
Algorithm $$$2$$$:
- Look at the picture for some time (between $$$1$$$ second and $$$5$$$ minutes), understand what's going on, understand the solution.
- Implement the solution.
- Re-read the editorial carefully. Ask yourself why the proof is so long. In particular, why do we need "Keep swapping endpoints until you get the "regular" bracket matching. You can show that the process ends in a finite number of steps"? Can't you just swap a single pair of endpoints to show that intersecting segments are never optimal?
- Read the comments; find out that many people tried to sort $$$l$$$ and $$$r$$$ in ascending order. Realize a fun fact: sorting $$$l$$$ and $$$r$$$ in ascending order is the worst possible ordering (assuming you sort $$$c$$$ correctly).
Conclusions
Editorials are not evil! But, if you are not improving, ask yourself if you are reading them correctly.









 Ciao, Codeforces! We're glad to invite you to take part in
Ciao, Codeforces! We're glad to invite you to take part in