Statement
We are given an array $$$a$$$ of length $$$n$$$. For some reason, we need answer $$$q$$$ queries. For the $$$i$$$-th, we need to return the contiguous subarray $$$a[l_i, r_i]$$$ of size $$$k_i=r_i-l_i+1$$$ in sorted order.
Solutions
Naive solution: $$$O(1)$$$ preparation, $$$O(klog(k))$$$ per query
We can just copy the subarray and sort it using various sorting algorithms. Using comparison sorting algorithms (quick sort, merge sort, std::sort, ...) will get us $$$O(klog(k))$$$. Using distribution sorts (radix sort, counting sort, ...) will get us $$$O(k\times constant)$$$ but these are generally not much better than comparison sorts due to high constants.
Merge sort tree: $$$O(nlog(n))$$$ preparation, $$$O(log(n)+klog(k))$$$ or $$$O(log(n)+klog(log(k)))$$$ or $$$O(log(n)+k)$$$ per query
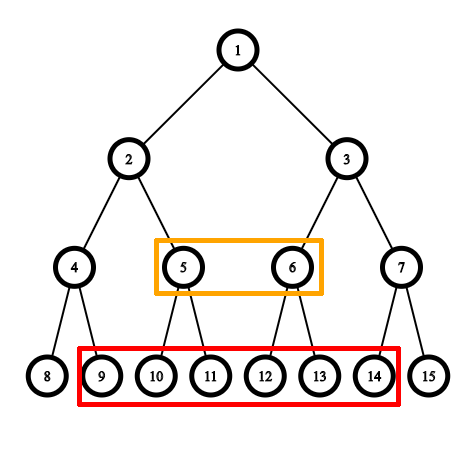
To make the math easier to work with, we will assume that the segment tree is a Perfect Binary Tree.
Recall that when querying a range of size $$$k$$$, we need at most $$$2log_2(k)=O(log(k))$$$ nodes to completely represent the range $$$[l, r]$$$$$$(r=l+k-1)$$$. Further more, we will have at most 2 nodes that have size $$$2^i$$$ for each $$$0\leq i <log(k)$$$.
Using a merge sort tree, we can obtain $$$O(log(k))$$$ sorted subarrays that together represent the range. Doing this take $$$O(log(n)+log(k))=O(log(n))$$$. We need to somehow merge these sorted subarrays into one sorted subarray.
If we just merge the subarrays one by one randomly, we'll need $$$O(klog(k))$$$ because we need to merge $$$O(log(k))$$$ times, each time we need $$$O(k)$$$ to merge. This is even worse than the naive solution because we need to spend $$$O(log(n))$$$ to get the subarrays.
We can try to merge all the arrays at the same time. To do this, we need to find the correct value among $$$O(log(k))$$$ values from each array. Using a priority queue (std::priority_queue, std::set, heap, ...), we can get this value in $$$O(log(log(k)))$$$ each time and get $$$O(klog(log(k)))$$$ to merge all of them. Total complexity per query is then $$$O(log(n)+klog(log(k)))$$$.
To do better, realize that when we merge the subarrays one by one, we can choose the order in which we merge them and potentially get a better run time. Because we have at most 2 nodes of each size $$$2^i$$$ for $$$0\leq i < log(k)$$$, if we always merge two smallest subarrays the total complexity is $$$O(k+log(n))$$$.
[Featured solution] Alternative Merge sort tree: $$$O(nlog(n))$$$ preparation, $$$O(log(n)+k)$$$ per query.
This solution deal with merging subarrays by reducing the number of subarrays we need to merge instead of trying to merge them in a good way.
If we also store the original indices of the sorted elements in each node, for a query $$$[l, r]$$$ we can answer it by iterating over the sorted elements and only keep the elements with indices inside $$$[l, r]$$$. This is, however, $$$O(n)$$$.
If the size $$$k=r-l+1$$$ is big enough compared to $$$n$$$ (i.e. $$$k/n \geq constant$$$) then the operation complexity is also $$$O(k)$$$.
We can then try to reduce the number of nodes we need to merge by iterating instead of going to children nodes when the queried range is big enough compared to the node size.
The segment tree model will then be something like:
If the queried range contains no element in this node, return nothing.
If the queried range contains at least $$$constant$$$ of the total amount of elements in this node, iterate the current note and return the correct sorted subarray.
Otherwise, go to the children node and do find the sorted subarrays and merge them.
If we choose the $$$constant=\frac{1}{2}$$$, there is at most 2 nodes we need to iterate. Iterating and merging the results from these nodes will take $$$O(k)$$$ and make the complexity for each query $$$O(log(n)+k)$$$.
Applications
Due to its linear to query size complexity, these algorithms probably have very little usage (if any) in Competitive programming. They probably can only be used on problems with a big restriction on the sum of queries size ($$$O(n\sqrt{n})$$$ for example).
One problem in which we can try to use the above algorithms is 963D - Частота строки but we have to answer the queries online.
Author's notes
963D - Частота строки was the inspiration for me to search for an algorithm to answer this type of query.
I couldn't find any tutorial/algorithm online (maybe I didn't search hard enough) so I tried making my own and it worked. I thought I should share them with you despise their apparent unusefulness. I have likely missed some potential applications (problems that can be solved), so please try looking for them and please share with us if you do find any.
If you find any mistake, please let me know. If you do know any efficient algorithm to answer this type of query (or related ones) please share with us.
Special thanks to:
- JettyOller for answering my questions about Suffix Automaton.
- You for reading this blog.