[problem:440884A]
Try what can you achieve with the given operation.
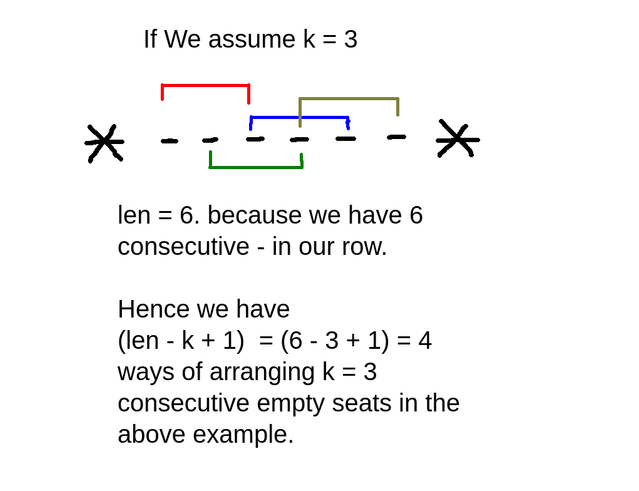
Given a sequence of numbers, the minimum value that can be obtained by applying the given bitwise AND operation is a1 & a2 & a3 & ... & an, since ANDing can't turn on any off bits but can only turn off on bits. By repeatedly applying the operation on suitable intervals, Mocha can make each number in the sequence a1 & a2 & a3 & ... & a4 . This can be achieved by performing the operation on each l, r possible pairs.
[submission:203874032]
[problem:440884B]
Try graph/tree traversal.
To solve this problem, we represent the repost chain as a directed acyclic graph (DAG), where each node represents a user and a directed edge from node A to node B represents a repost event where user A reposted from user B. We use a recursive DFS algorithm to traverse the DAG and find the longest path. We start by adding the initial post by Polycarp as the root node of the DAG and then iterate through the repost events in the input, adding each user to the DAG with a directed edge from the reposting user to the original poster. We then use a recursive DFS function to traverse the DAG and find the length of the longest path from the root node to any other node. Finally, we return the maximum length of any path in the DAG, which corresponds to the length of the longest repost chain.
BFS Solution [submission:204222640] DFS Solution [submission:204117650]
[problem:440884C]
This problem can be solved using a graph traversal algorithm such as Breadth-First Search (BFS). We can create an undirected graph where each stamp represents an edge between two cities. Then we can start BFS from any city and traverse the graph until we find one of the end cites, then
Since there are only two possible routes, we can stop BFS once we find a path that connects the two endpoints. We can then output the indexes of the cities along this path.
Overall, the time complexity of this solution is O(n), where n is the number of stamps in the envelope.
[submission:204338953]
[problem:440884D]
Run BFS to find the a path between start cell and the lower rightmost cell.
[submission:203876708]
Try to solve without graph traversal.
[problem:440884E]
Start from the end position of the mouse's move and return all cells that are p distance away from it.
[submission:203836678]