All teams received an email stating that only onsite teams attending World Finals in Russia would be eligible for medals. The remote teams would be placed in a separate "open division" that would not be eligible for medals but would get titles such as "high honors" and "honors". This last minute change has left us reconsidering our decision to compete remotely.
You also need to be fully vaccinated (with proof of vaccination) to be able to attend World Finals in Russia.








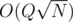
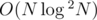 by maintaining a set in each node and merging the smaller set into the larger ones.
by maintaining a set in each node and merging the smaller set into the larger ones. 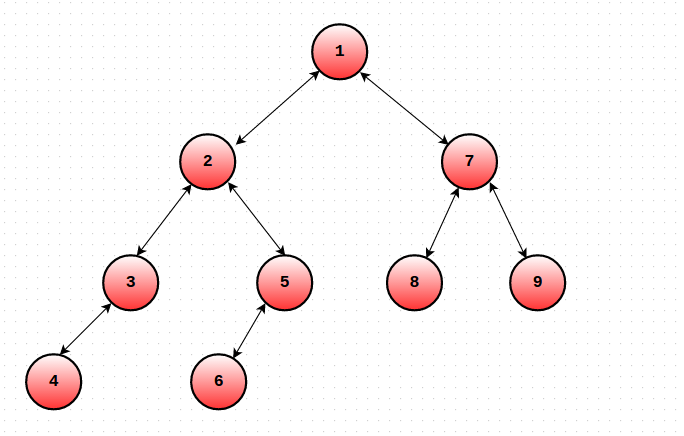
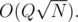 This modified DFS order works brilliantly to handle any type path queries and works well with Mo's algo. We can use a similar approach to solve many types of path query problems.
This modified DFS order works brilliantly to handle any type path queries and works well with Mo's algo. We can use a similar approach to solve many types of path query problems. 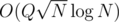 by using the above technique and maintaining a BIT or Segment Tree.
by using the above technique and maintaining a BIT or Segment Tree.
