Hello codeforces! Recently I was solving solar storm from NOI 2020's preliminary round on oj.uz. I made the following submission, which unfortunately WAed.
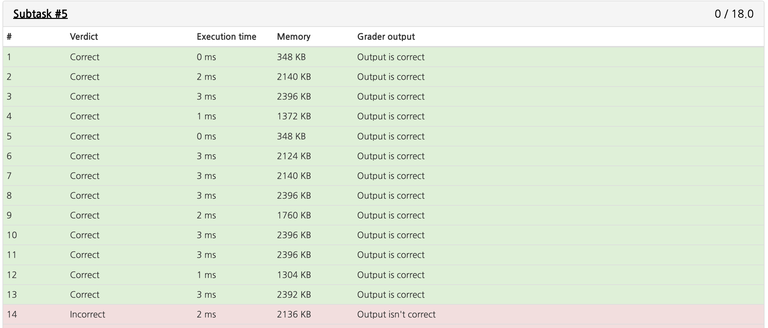
So I tried debugging it. I made several attempts, after which I decided to just look at the test data to see what I was failing. And this is the weirdest part, according to the official checker, my answer for 5-14 matches the optimal answer.

Multiple AC codes gave the exact same output that mine is givng.
(Note that I did also use the checker, and it also said that my answer was right.)
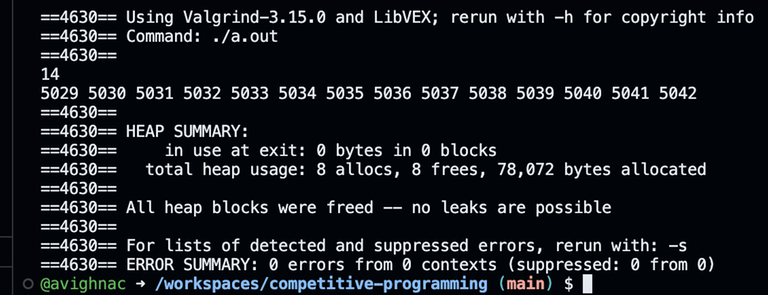
So then I thought of the next obvious issue: some kind of undefined behaviour? I checked this using valgrind (after commenting out my fast IO), and, unfortunately, there is none.
I also looked at the code of some AC submissions, and thier logic is almost identical to mine, so at this point, I really have no clue what I'm doing wrong, or what I can even do to debug this further (is there some way to see what my code was outputting when it received the wrong answer?) Please let me know if you do. Thank you!