This is my solution to the problem 167D - Wizards and Roads, which I wanna to explain in a more detailed way. First, thanks to Dmitry_Egorov and I learned the solution to this problem from his blog.
But I tried a lot by myself because maybe I can not quite understand some details of Dmitry_Egorov's proposed solution.
Link:http://codeforces.com/blog/entry/4214
First one, I wanna to talk about the Cartesian tree. A Cartesian tree is a tree which behaves like a binary search tree and also a heap. We name the variable regarding the BST property "KEY" and name the variable regarding the heap property "VALUE"; So, VALUE of every node is less (or more) than the VALUEs of its sons. KEY of every node is more than KEY of its left node and less than KEY of its right node. Talking about this special property, you may find out that: the smallest VALUE between L and R can be found by finding LCA of two nodes which have KEY as L and R respectively.
If given a list of VALUEs and KEYs, how to build a Cartesian tree.? First, we can sort the array in regard of KEY. And we insert node into the tree in the increasing order of KEY : Because the node which is ready to insert is bigger than all the nodes which have been inserted before when comparing their KEYs, the new node will on the very right side of the tree. In order to find a proper place to insert the node (where the heap property can be satisfied), we will examine the nodes along the very right side and find the first node that has a VALUE less than the VALUE of the new node. Thus, we will add the new node there, as a right son of the father of the previous node. And link the previous node (including all the subtrees) to the left of the new node, (leaving the right son of the new node blank).
We can use a stack to implement this process, which can be solved in O(N); Put every new node into the stack. If the new node has a VALUE larger then the VALUE of the node at the top of the stack: That's all, suspend it to the right of that node. And push the node in the stack. If not: Examine the node at the top of the stack, if its VALUE is larger than the VALUE of the new node, pop it. And the final node which is poped from the stack is the "PREVIOUS NODE" mentioned above, One more thing, If at this moment, the stack is empty, the new node will be the current root. (So no more work will be done on the father of the "PREVIOUS NODE")
Return to the problem now: According to the problem, the roads and cities can be established in the way like a tree. This tree is a Cartesian tree because the tree node has two variables: X is something like KEY, has the property of BST Y is something like VALUE, has the property of Heap; The edges are built in this way: Find the highest point (regarding to the biggest Y) and link it to the highest point towards left and towards right. And do the same to the left and right part.
For the X,Y showed below, for example, we can build a tree like this: 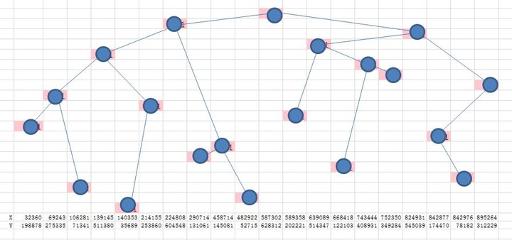
The way to build the tree is the same as the way to build a normal Cartesian tree. And considering the queries(L and R) We gonna to find the very left node in the segment and the very right node. Suppose they are L0 and R0; From L0 and R0, go upward along the tree. But we need to pay attention to this process, we may temporarily leave the segment but finally return to some node in the segment We need to modify the son information of that node, skip the nodes outside the segment, directly pointing to the lateset node in the segment. And we need to save all the modified nodes because when we start process a new query, all the information should be restored.
To get the answer, we can use a very simple DP method. Donate DP0[X] is the answer if we do not take node X into account DP1[X] is the answer if we take node X into account. Thus,
DP0[X]=DP0[Leftson of X]+DP0[Rightson of X]
if X has a leftson:
DP1[X]=DP0[Leftson of X]+DP1[Rightson of X]+1
if X has a rightson:
DP1[X]=DP1[Leftson of X]+DP0[Rightson of X]+1 (Find the max of the following two values)
Finally,Good luck to solve this problem.










