Hello, I'd like to share a cool trick, i came across recently. No doubt some people will be familiar with this, but i believe many won't be, simply because when it comes to Lazy Propagation most people use segment trees in contest. This method, although not as flexible, is far simpler. Not to mention a lot easier to code with a lot less lines of code. Also while Fenwick Tree and Segment Tree have the same complexities, in practice Fenwick Tree is usually faster.
Before we begin, I'd like to say that you should have at least a decent understanding of binary indexed trees (BITs).
We know by now, that BIT can be used to support following two operations:
1) Query(i) — queries element at position i.
2) Update(i, j, d) — adds d to the elements from i to j.
Some people call this "range update, single query", what we would like to accomplish is "range Update, range Query".
1) RangeQuery(i, j) — returns the sum from i to j.
2) RangeUpdate(i, j, d) — adds d to the elements from i to j.
Just to illustrate RangeUpdate function suppose our array has 5 elements, all initialized to zero, and we call RangeUpdate(2, 3, 3). Our array should turn from {0, 0, 0, 0, 0} to {0, 3, 6, 6, 6}.
In order to achieve this we'd need to examine what should happen when we call the function Update(i, j, d). For some arbitrary index, denoted as idx, we can differentiate three cases:
Case 1) idx < i, these elements remain unchanged.
Case 2) i ≤ idx ≤ j, element at index i is increased by d, element at index i + 1 is increased by 2·d and so on... So element at index idx is increased by (idx - i + 1)·d = idx·d - (i - 1)·d.
Case 3) idx > j, every element here is increased by a constant amount, (j - i + 1)·d = 0·idx - ( - j + i - 1)·d.
Here i have intentionally written values at every index as idx·C1 - C2, where C1 and C2 are constants and idx is the only independent variable. We can use two BITs to keep track of C1 and C2 values, let's call them bitAdd and bitSub, and our answer is simply idx·bitAdd.Query(idx) - bitSub.Query(idx).
Finally to put it all together here is how we are going to implement lazy propagation:
RangeUpdate(i, j, d):
Case 1) idx < i, we do nothing with bitAdd and bitSub, since elements here don't change.
Case 2) i ≤ idx ≤ j, we call bitAdd.upate(i, j, d) and we call bitSub.update(i, j, (i - 1) * d).
Case 3) idx > j, we only call bitSub.update(j + 1, n, ( - j + i - 1) * d).
RangeQuery(i, j):
We know that Sum[1..idx] = idx·bitAdd.Query(idx) - bitSub.Query(idx).
RangeQuery(i, j) = Sum[1..j] - Sum[1..i - 1]
Here is my (untested) implementation of the idea : http://ideone.com/mGlJs2
Please feel free to post any questions that you might still have, and to point out any spelling\grammar mistakes :)









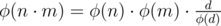 where
where 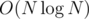 , is it possible to do it in
, is it possible to do it in 
