Hi,
I want to know is there any dynamic programming or any other approach to find if there is any subset with a given xor(just like we have dynamic programming approach to find if there is any subset with a given sum) ?
UPD: I have solved this problem with a similar approach to subset sum dynamic programming.











I know how to solve it, if your set contains only one number
You can solve this problem by solving system of linear equations(Gauss method) modulo 2.
x[i][j] = 1 if (a[i] & (1 << j) > 0) else 0.
BTW. Who know how calculate number of subsets with given xor?
2n - rank
Oh, thanks)
Hi Neodym,can you please explain a bit more or give some resource from where I can read this??
Thanks.
You should make linear transformations with your matrix(system of linear equations) — one string -> this string minus another string. Of course, all transformations modulo 2. Your goal is to get matrix with no more than one nonzero element in every column. So, some variables will depend on other variables (like x1 = x4 + x5) and some variables will independent. Number of this independent variables is a rank of matrix. Key words for search: "Gauss method", "matrixes", "system of linear equations".
hi Neodym,
So,if I solve the system of linear equations where left hand side is the matrix which represents all bits from each a[i] per row and right side the value (i.e the given xor) and if we can find the rank of that system of linear equation matrix by gaussian elimination,then no of subsets with the given xor will be 2^(n-rank) ?? Is my understanding correct??
Thanks a lot,by the way!!! :) you have really explained it nice. :) I just want to verify my understanding.
Assume each element in the set is of length m bits and there are n elements in the set. The linear system of equation represents AX = B. Now we have n rows and m columns in the left hand side matrix, A.
What does the vector X represent which has m rows? What is the right hand side vector which has n rows?
Can you please explain!
Update: Everything is clear for me now! A contains the elements in matrix form m x n (one column for each element in the set) B vector contains the given xor value m x 1 (one bit per entry) X vector contains the bool value if each element of set is present in subset or not (one entry per element in set)
@Neodym How did you get this result ?
I've been asked this question lots of times, and now I tried to give as most correct answer as I could.
Unfortunetely, codeforces latex redactor does not support all opportunities of tex, so I've shared a document on OneDrive.com: http://1drv.ms/1muktg0
Feel free to ask on it, maybe I'll update this document.
This link became broken for some unknown reason — maybe, OneDrive links are valid only for some short time? — and I was asked to post new valid link, so here it is:)
https://1drv.ms/b/s!AiYoGrthrGItf0x4zb00w17bKfQ
As usual, feel free to ask me anything=)
Thanks a LOT for This.
You can also look at the editorial for XorCards problem. It has a nice explanation there.
Hi sping128,Thanks a lot. Topcoder tutorials always explain it very nicely.Thanks again :) Though I have solved this particular one in SPOJ without gauss-jordan,but I really want to learn how to use gauss-jordan to solve such problems.
Similar problem: SPOJ-XMAX
this can be solved very easily using just recursion + memoization. no need of Gauss method or any such thing.
if u assume that
iis the current index andmaskis the XOR of all elements currently in the set, the recursive function will look likeint solve (int i, int mask). all u need to do is addsolve(i+1, mask^a[i])(no of subsets if we add the current element to the set) andsolve(i+1, mask)(no of subsets if we don't add it).ofcourse u need to memoize this to reduce the time complexity from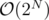 to
to 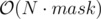 .
.
I got AC this way only.But I think mostly xor related problems are to be done with gaussian elimination,so it'll be better to learn that :)
i have applied this idea but getting wrong ans on judge at 5 test case can you help
include<bits/stdc++.h>
using namespace std;
define LL long long
LL MIN = -1;
LL arr[100009]; LL val[100009];
int n;
LL dp(int i){ if(i==n){return 0LL;} if(val[i] != MIN){return val[i];}
}
int main(){ #ifndef ONLINE_JUDGE freopen("input.in","r",stdin); freopen("output.out","w",stdout); #endif
}
It would be nice if someone shares their code using gaussian elimination as it would serve a great reference.
Here I used Gauss elimination to calculate determinant in Java: http://codeforces.com/blog/entry/19750
Here is C++ code for solving system of equations: http://e-maxx.ru/algo/linear_systems_gauss
This problem(find a subset with given xor) can be solved in log^2 maxA using linear basis.
Can u send some reference for that. Thanks in advance