1689A - Lex String
Author: wxhtzdy
Greedily take the smallest character in both strings. What's the exception to this?
We can't take the smallest character in both strings when we've already took $$$k$$$ elements from the string we chose. Denote $$$A$$$ as the number of characters we've took from string $$$a$$$ in the last few consecutive moves and denote $$$B$$$ the same for $$$b$$$. If $$$A=k$$$, then we have to take the smallest character in string $$$b$$$ instead of possibly $$$a$$$. If $$$B=k$$$, then we have to take the smallest character in string $$$a$$$ instead of possibly $$$b$$$.
Remember to reset $$$A$$$ to $$$0$$$ when you take a character from $$$b$$$. Similarly, reset $$$B$$$ to $$$0$$$ when you take a character from $$$a$$$.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t; cin>>t;
while (t--)
{
int n,m,k; cin>>n>>m>>k;
string a,b,c; cin>>a>>b;
sort(a.begin(),a.end(),greater<char>());
sort(b.begin(),b.end(),greater<char>());
int ak=0,bk=0;
while (!a.empty() && !b.empty())
{
bool gde=b.back()<a.back();
if (gde && bk==k) gde=0;
if (!gde && ak==k) gde=1;
if (gde) c.push_back(b.back()),bk++,ak=0,b.pop_back();
else c.push_back(a.back()),ak++,bk=0,a.pop_back();
}
cout<<c<<"\n";
}
}
1689B - Mystic Permutation
Author: n0sk1ll
When is it impossible to find such permutation?
It is impossible only for $$$n=1$$$. In every other case, iterate over each position in order from $$$1$$$ to $$$n$$$ and take the smallest available number. What's the exception to this?
The exception is the last two elements. We can always take the smallest available number for each $$$q_i$$$ satisfying $$$i<n-1$$$. To do this we maintain an array of bools of already taken numbers, and then iterate over it to find the smallest available number satisfying $$$p_i\neq q_i$$$ which is also not checked in the array, and then check it (we took it).
Now consider $$$(p_{n-1},p_{n})$$$ and we want $$$(q_{n-1},q_{n})$$$ to be lexicographically minimal while satisfying $$$p_{n-1}\neq q_{n-1}$$$ and $$$p_{n}\neq q_{n}$$$. Let $$$a$$$ and $$$b$$$ be the last two unused numbers in the array of bools with $$$a<b$$$. We try to take $$$(q_{n-1},q_{n}) = (a,b)$$$. If $$$a=p_{n-1}$$$ or $$$b=p_{n}$$$, then we take $$$(q_{n-1},q_{n}) = (b,a)$$$. If $$$(a,b)$$$ isn't valid, then $$$(b,a)$$$ is. The proof is left as an exercise to the reader.
This solution runs in $$$O(n^2)$$$ and can be optimized to $$$O(n \ log \ n)$$$.
#include <bits/stdc++.h>
using namespace std;
bool took[1005];
int p[1005];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t; cin>>t;
while (t--)
{
int n; cin>>n;
for (int i=1;i<=n;i++) cin>>p[i];
for (int i=1;i<=n;i++) took[i]=0;
if (n==1)
{
cout<<"-1\n";
continue;
}
for (int i=1;i<=n-2;i++)
{
int k=1;
while (took[k] || k==p[i]) ++k;
cout<<k<<" "; took[k]=1;
}
int a=-1,b=-1;
for (int i=1;i<=n;i++) if (!took[i])
{
if (a==-1) a=i;
else b=i;
}
if (a!=p[n-1] && b!=p[n]) cout<<a<<" "<<b<<"\n";
else cout<<b<<" "<<a<<"\n";
}
}
#include <bits/stdc++.h>
using namespace std;
int t,n,A[1010],B[1010];
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(int i=1; i<=n; i++)
{
scanf("%d",&A[i]);
B[i] = i;
}
if(n==1)
{
printf("-1\n");
continue;
}
for(int i=1; i<n; i++)
{
if(A[i]==B[i]) swap(B[i],B[i+1]);
}
if(A[n]==B[n]) swap(B[n-1],B[n]);
for(int i=1; i<=n; i++) printf("%d ",B[i]);
printf("\n");
}
return 0;
}
Riblji_Keksic found the O(n) solution.
1689C - Infected Tree
Author: n0sk1ll
We always delete a vertex directly connected to an infected one.
Use dp.
Let $$$u_1,u_2,...,u_k$$$ be the sequence of removed vertices such that the infection cannot spread anymore. If vertex $$$u_i$$$ was never directly connected to an infected vertex, then we could have deleted its parent instead of $$$u_i$$$ and we would have got a better solution. Hence, we may assume we always delete a vertex directly connected to an infected one.
Now, we may use some dynamic programming ideas. Let $$$dp_i$$$ be the maximum number of vertices we can save in the subtree of vertex $$$i$$$ if that vertex is infected and we use operations only in the subtree. We can assume the second as the tree is binary and we have two choices — save the subtree of one child by deleting it and infect the other, or the other way around. In each case, the infection will be "active" in at most one subtree of some vertex.
If $$$c_1$$$ and $$$c_2$$$ are the children of vertex $$$i$$$, the transition is
where $$$s_i$$$ denotes the number of vertices in the subtree of $$$i$$$.
The answer to the problem is $$$dp_1$$$. Complexity is $$$O(n)$$$.
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> g(300005);
int ch[300005],dp[300005];
void dfs(int p, int q)
{
ch[p]=1,dp[p]=0; int s=0;
for (auto it : g[p]) if (it!=q)
{
dfs(it,p); s+=dp[it];
ch[p]+=ch[it];
}
for (auto it : g[p]) if (it!=q)
{
dp[p]=max(dp[p],s-dp[it]+ch[it]-1);
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t; cin>>t;
while (t--)
{
int n; cin>>n;
for (int i=1;i<=n;i++) g[i].clear();
for (int i=1;i<n;i++)
{
int u,v; cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1,0);
cout<<dp[1]<<"\n";
}
}
1689D - Lena and Matrix
Author: n0sk1ll
There are not a lot of useful black squares.
Consider this algorithm: iterate over all squares in the matrix and find the most distant black square.
Let's find out how to do that efficiently. In fact, only 4 (not necessarily distinct) black squares will be useful: one square which minimizes $$$i-j$$$, one square which maximizes $$$i-j$$$, one square which minimizes $$$i+j$$$ and one square which maximizes $$$i+j$$$, where $$$(i,j)$$$ denotes the black cell's coordinates. In other words, we would like to find the most distant "border".
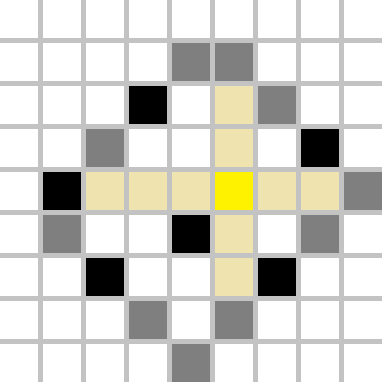
Let's look at the example above. The cell we choose to recolour to yellow creates four regions (the top-left rectangle, the top-right rectangle, the bottom-left rectangle and the bottom-right rectangle, which are created by two lines parallel with coordinate axes passing through our yellow point). The most distant border will be fully contained inside one region, hence we should find the distance from our yellow cell to any cell on that border, and that is the maximum possible distance.
The complexity is $$$O(n\cdot m)$$$.
#include <bits/stdc++.h>
using namespace std;
char tab[1003][1003];
pair<int,int> a={-1,-1},b={-1,-1},c={-1,-1},d={-1,-1};
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t; cin>>t;
while (t--)
{
a={-1,-1},b={-1,-1},c={-1,-1},d={-1,-1};
int n,m; cin>>n>>m;
for (int i=0;i<n;i++) cin>>tab[i];
vector<pair<int,int>> interesting;
for (int i=0;i<n;i++) for (int j=0;j<m;j++) if (tab[i][j]=='B')
{
if (a.first==-1 || i+j>a.first+a.second) a={i,j};
if (b.first==-1 || i+j<b.first+b.second) b={i,j};
if (c.first==-1 || i-j>c.first-c.second) c={i,j};
if (d.first==-1 || i-j<d.first-d.second) d={i,j};
}
interesting.push_back(a);
interesting.push_back(b);
interesting.push_back(c);
interesting.push_back(d);
int ans=1e9; pair<int,int> opt;
for (int i=0;i<n;i++) for (int j=0;j<m;j++)
{
int dist=0;
for (auto it : interesting) dist=max(dist,abs(i-it.first)+abs(j-it.second));
if (dist<ans) ans=dist,opt={i,j};
}
cout<<opt.first+1<<" "<<opt.second+1<<"\n";
}
}
1689E - ANDfinity
Author: wxhtzdy
Increase every $$$0$$$ by $$$1$$$ initially.
Check if the answer is $$$0$$$: check whether the graph is already connected.
Check if the answer is $$$1$$$.
If the answer is not $$$0$$$ or $$$1$$$, then it is $$$2$$$.
Firslty, let's understand how to check whether the graph induced by some array $$$b$$$ is connected in $$$O(n \ log \ max \ b_i)$$$. We create a graph over bits. Let's take all elements $$$b_i$$$ and add an edge between their adjacent bits (all bits of a single $$$b_i$$$ will be connected). To quickly access the lowest bit we will use $$$b_i \ \& \ -b_i$$$ in code. Now we just check whether the graph over bits is connected.
We check whether the graph for initial array $$$a$$$ is connected. If it is, the answer is 0.
Then, we wonder if the answer is $$$1$$$. Check if at least one of the graphs for arrays $$$a_1,...,a_{i-1},a_i-1,a_{i+1},...,a_n$$$ for every $$$1\leq i \leq n$$$ is connected. Do the same for arrays $$$a_1,...,a_{i-1},a_i+1,a_{i+1},...,a_n$$$. If none of the graphs is connected, the answer is $$$2$$$ and otherwise $$$1$$$.
Now let's see how the answer will be at most $$$2$$$. Let $$$i_1,i_2,...,i_k$$$ be the sequence of indices denoting that $$$a_{i_j}$$$ has the highest lowest bit (the highest value of $$$a_i \ \& \ -a_i$$$). if $$$k=1$$$ then we can just decrease $$$a_{i_1}$$$ by $$$1$$$ and connect everything. If $$$k\geq 2$$$ and we do the same we might disconnect that number from other numbers having the highest lowest bit, thus an additional operation of adding $$$1$$$ to $$$a_{i_2}$$$ is needed to keep everything connected. The answer is $$$2$$$ in this case.
Complexity of this solution is $$$O(n^2 \ log \ max \ a_i)$$$.
#include <bits/stdc++.h>
using namespace std;
int a[2005];
vector<vector<int>> g(32);
bool vis[32];
void dfs(int p)
{
if (vis[p]) return; vis[p]=1;
for (auto it : g[p]) dfs(it);
}
bool connected(int n)
{
int m=0;
for (int i=0;i<n;i++) if (a[i]==0) return false;
for (int i=0;i<n;i++) m|=a[i];
for (int i=0;i<31;i++) g[i].clear();
for (int i=0;i<n;i++)
{
int last=-1;
for (int j=0;j<31;j++)
if (a[i]&(1<<j)){
if (last!=-1) g[last].push_back(j),g[j].push_back(last);
last=j;
}
}
for (int j=0;j<31;j++) vis[j]=0;
for (int j=0;j<31;j++) if ((1<<j)&m)
{
dfs(j); break;
}
for (int j=0;j<31;j++) if (((1<<j)&m) && !vis[j]) return false;
return true;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t; cin>>t;
while (t--){
int n; cin>>n;
for (int i=0;i<n;i++) cin>>a[i];
int ans=0;
for (int i=0;i<n;i++) if (a[i]==0) ans++,a[i]++;
int m=0;
for (int i=0;i<n;i++) m=max(m,(a[i]&(-a[i])));
if (connected(n))
{
cout<<ans<<"\n";
for (int i=0;i<n;i++) cout<<a[i]<<" "; cout<<"\n";
goto kraj;
}
for (int i=0;i<n;i++)
{
a[i]--;
if (connected(n))
{
cout<<ans+1<<"\n";
for (int i=0;i<n;i++) cout<<a[i]<<" "; cout<<"\n";
goto kraj;
}
a[i]++;
}
for (int i=0;i<n;i++)
{
a[i]++;
if (connected(n))
{
cout<<ans+1<<"\n";
for (int i=0;i<n;i++) cout<<a[i]<<" "; cout<<"\n";
goto kraj;
}
a[i]--;
}
for (int i=0;i<n;i++) if ((a[i]&-a[i])==m)
{
a[i]--;
break;
}
for (int i=0;i<n;i++) if ((a[i]&-a[i])==m)
{
a[i]++;
break;
}
cout<<ans+2<<"\n";
for (int i=0;i<n;i++) cout<<a[i]<<" ";
cout<<"\n";
kraj:;
}
}










Very fast editorial. Problems were good also.
Problem were really good, thanks [user:n0sk1||] and wxhtzdy and all the contributors of the contest. I was really a good contest for me.
I was not even able to solve A :(
It's OK
Don't worry. I also felt that A was tougher than usual.
Why DP in C? It's just overcomplication, isnt it?
UPD: Idk, i just... Bruh
what's your approach?
You can check out my solution https://codeforces.com/contest/1689/submission/160137279 . The idea is that we can make the infection infect only one vertex at a time, or non at all, If the vertex has two children, we delete one of them and make the infection spread to the other child, so both children die, and this process continues unless one of their children has only one child so infection can not spread anymore, then you just cut one source and infection can not spread at all.
What is the use of variable 'dis' in your code and why are you returning (dis+1) at some places, (dis+2) at other places, and just (dis) at some other places?
Can you please explain a bit?
It denotes the amount of vertex that dies, so if the vertex has two children, both of them die, so I do dis+2, if it only has one, only one dies, if it has none, then none dies and I just return dis.
You can just simply use recursion. My solution: https://codeforces.com/contest/1689/submission/160139911
ig we can just store subtree count of every node & later add by processing in valid manner
yep, but is that not already considered dp?
we can solve c without dp.the approch is simply follow along the infected path along the binary tree using dfs/bfs,take minimum of the available infected paths and saved =(n-(infected)) my solution approch
Can anyone see why WA. 3rd Problem I'm storing the child counts in visited and then moving optimally along less children. 160139740
you counter a case when the children is equal Thats the case when your approach doesn't work that's why we use dp to store both possible path and take the max
hello can you see my code?why my code WA3, i coudln't find mistake,Thanks!
https://codeforces.com/contest/1689/submission/247737811
Why do you multiply s by 2 here?
mx=min(mx,(2*s)-1);can you please explain me the logic of 2*s -1 and 2*s in leaf node case and 2degree node respectively
Agreed. For anyone who isn't aware, the non-DP approach is to let $$$v$$$ be the least deep vertex with at most one child. Then, the number of vertices that must be lost is $$$d(v) + c(v) + 1$$$, where $$$d(v)$$$ is the depth of $$$v$$$ (where the root has depth $$$1$$$) and $$$c(v)$$$ is the number of children of $$$v$$$.
I am probably being stupid, but why is d(v) being multiplied by 2?
For each two-child vertex down which the virus spreads, you lose both the child onto which the virus spreads and the other child, which you must shut down to keep the virus from spreading onto the other branch.
Got it, thank you
whats the proof for this?
After reading Geothermal's second comment, I had to think carefully and visualize a tree that had layers of two-child vertices followed by a single- or no-child vertex. Then it became clear.
I hate you, i really hate you people
fastest editorial ever? nice
very fun, wish I could do more than 3
I don't think so there was recently a contest in which they update the rating and the editorial was out the minute contest and system testing ended. It was Instant no delay.
In problem C, wish there was a test case in the sample, where the input had an edge connecting from child node to parent node.
Initially I assumed that, the edges were always from parent to child, and wasted time.
I know it is my fault for making wrong assumption. But still
:(.I wasted half of my time trying to code a greedy algorithm, and only realized halfway through that it was supposed to be dp, so that was kinda sad lol.
Cool
O(n) solution for B.
The smallest possible lexicographic permutation is 1,2,3,4... Assume that this is the answer. Now just check if any element of the answer array matches with input permutation. if yes, swap it with next element. It's easy to see that no conflict would arise in this manner. There's edge case for last index, we have to swap it with previous element.
My submission- https://codeforces.com/contest/1689/submission/160104354
The problem IDs in the editorial are shown as the gym IDs (probably, some testing mashup). Please fix it.
Fixed, sorry.
balanced round with good problems keep it up
cool problems and well organized overall a very good contest.thanks:)
Problem C can be solved greedily. I just find the shortest path from root to the node which have less than 2 children and infected those node and saved all other nodes by deleting the first node of every subtree connected to these infected nodes.
Nice Observation! What is cnt in your code?
cnt represent that the last node has any child or not . If the last node has no child then there is no subtree connected to that node and in that case there is one less node to delete. That's why when cnt is 1(no child) the output is n-2*(ans+1)+1 which is equal to n-(ans+1)-ans and in the case where cnt is 2(has one child) the output is n-2*(ans+1)
I solved C absolutely the same way as you
what does this part of the code do?
If sz is less than 3 this means that the node has only one child or no child so the path ends here and I am just taking the minimum of all the path from root to the node having no or one child and cnt just stores that the last node has a child or not
Why is this getting MLE ?
My code for C : 160135752
Your solve function is called recursively infinite times as it is calling its parent node in some test cases like the below one.
Fixed , thank you !
Still , it is curious why it got MLE instead of TLE in this case.
The hint 3 in problem E tells that answer is 0, 1 or 2. But we have an answer
3in the example.Perhaps they exclude the mandatory "+1" to the zeros initially
Can someone please explain problem C? Since it is a binary tree there will always be at max two edges from the root node. I calculated the indegree of both and subtracted the minimum to find the max nodes which can be saved but this approach is giving wrong answer on test 3. Pls Help
https://p.ip.fi/4svQ
I'm not sure what you mean but you can make more than 1 saving move
they didn't thought that C can be solved using DFS?
For D, another approach is to use the fact that $$$abs(x) = max(x, -x)$$$.
Let $$$S$$$ be the set of black cell, then we need to minimize: $$$max(abs(i - x) + abs(j - y))$$$ for every combination of $$$1\leq i \leq n, 1\leq j \leq m, (x, y) \in S$$$.
This is just $$$max(max(i - x, x - i) + max(j - y, y - j))$$$.
Just expand the inner $$$max$$$ and we will have 4 cases to check, similar to the official tutorial.
160104327
I think this idea ($$$abs(x) = max(x, -x)$$$) is pretty common but still very powerful, probably would have taken much more time to solve D if I didn't know it.
When I tested the round, I immediately recognized the problem as one where you need to transform the coordinates in such a way that the Manhattan metric becomes the Chebyshev metric (which corresponds to rotation by 45 degrees and appropriate scaling). $$$|x| = \max \{x, -x\}$$$ is basically why that transformation works. I was also opposed to adding this problem in the contest because 1658E - Gojou and Matrix Game is a strictly harder version of the problem.
In the 4 cases that we make on expanding the max, there is an underlying condition for every case right, for example, only when $$$i \leq x$$$ and $$$j \leq y$$$, we get the Manhattan distance as $$$x + y - (i + j)$$$, but in your implementation, you have directly chosen the maximum value of $$$x + y$$$, (say it is $$${(x+y)}_{max}$$$) and you've taken the maximum of $$$cost$$$ and $$$(x+y)_{max} - (i+j)$$$ without checking if $$$i\leq x$$$ and $$$j\leq y$$$. Can you please explain the thought process behind this and why this works?
Edit: I misunderstood what you meant by "expanding the inner max", I got it now, thanks.
Yes, writing out the expansion more explicitly for anyone who doesn't see it, it is equal to $$$\max_{(x,y) \in S} \max(i-x+j-y,i-x+y-j,x-i+j-y,x-i+y-j)$$$ $$$= \max( \max_{(x,y) \in S} (i-x+j-y), \max_{(x,y) \in S} (i-x+y-j), \max_{(x,y) \in S} (x-i+j-y), \max_{(x,y) \in S} (x-i+y-j))$$$ $$$= \max(i+j + \max_{(x,y) \in S} (-x-y), i-j + \max_{(x,y) \in S} (-x+y), j-i + \max_{(x,y) \in S} (x-y), -i-j + \max_{(x,y) \in S} (x+y) ),$$$ and you can precompute each of the four terms $$$\max_{(x,y) \in S} (ax + by)$$$ for $$$a,b \in {-1,1}.$$$
Can we use a similar method when we need to find the minimum Manhattan distance among all pair of points? Just replacing the outer MAX by MIN, whereas inner MAX remains same, as it corresponds to the 'abs' thing.
I think a simpler solution is to transform the Manhattan distance to Chebyshev distance, and we only need to minimize $$$\max_{1\le i\le k} {\max(|a'-x_i'|,|b'-y_i'|)}=max(\max_{1\le i\le k}|a'-x_i'|,\max_{1\le i\le k}|b'-y_i'|)$$$, which is optimal when choosing the median among the $$$x$$$ and $$$y$$$ coordinates of given points.
Sorry, I didn't see that the tester above had already shared this solution.
Problem D can also be solved by dp.
But we have to maintain 4 dp tables. One table dp[i][j] stores max distance of a black point from i,j in top left of the matrix and other tables will store for other three part of matrix which is top-right, bottom-left and bottom-right . Max distance of a point from black point will be max of the value from all four table and then we can take minimum of all these and that will be our answer .
Even just 2 dp tables are sufficient... One storing max distance of a black cell with x coordinate < i & other with x coordinate >= i for a given (i,j)
nice solution. I missed the idea of using first and last rows per column
can you explain more ? i didn't get what you mean by max dist. < i . Like what does this signify?
For each point (i,j), we want to know the max distance of a black cell from it. Once we know this, we can simply iterate over each (i,j) & find the one which is having min value. Now, for finding this, I define 2 dp tables :
dp1(i,j) : Max distance of a black cell from (i,j) considering all black cells with coloum no. < j.
dp2(i,j) : Max distance of a black cell from (i,j) considering all black cells with coloum no. >= j.
Now, let's try to build transition for dp1(i,j), it includes all black cells with coloum no. 0 to j-1. As per definition of dp1(i,j-1), it includes all black cells with coloum no. 0 to j-2.
So, now dp1(i,j) = max(1 + dp1(i,j-1), max distance of a black cell in (j-1)th coloum from (i,j)).
Similarly, dp2(i,j) = max(1 + dp2(i,j+1), max distance of a black cell in jth coloum from (i,j)).
Now, max distance of a black cell from (i,j) = max(dp1(i,j), dp2(i,j)). You can check out my code : here
Yaa. I do it with making 4 dp tables
I was thinking of applying a greedy approach for problem C, why is it not enough to find the closest path from root to leaf or a node which has just 1 children. after we find the path length we can just get the answer by (N — (x + (x-1)) + 1 ( 1 for the case if the last node found had 1 child).
What i was thinking is for every step we have two choices either remove one branch or the other, when we remove one branch we also delete a node, thus (x + (x-1)), these are the nodes removed or infected, after that just subtract this from total N.
The approach is wrong but i can;t figure out why, can someone help please?
Okay, got the error, the approach was right, the problem was i was BFS so i had to take care of the fact that if there are two nodes in which one has only one child and there is other node which does not have a child, i will go with the one which does not have a child and in that case the formula will be n-(x+(x-1)) only
From what I understand you are trying to say, your approach is correct! This is actually the same approach that Geothermal had: https://codeforces.com/submissions/Geothermal You may have had some calculation error. Here is what he had to say:
"Agreed. For anyone who isn't aware, the non-DP approach is to let v be the least deep vertex with at most one child. Then, the number of vertices that must be lost is d(v)+c(v)+1, where d(v) is the depth of v (where the root has depth 1) and c(v) is the number of children of v."
(Why is the depth multiplied by 2 in your code?) "For each two-child vertex down which the virus spreads, you lose both the child onto which the virus spreads and the other child, which you must shut down to keep the virus from spreading onto the other branch."
and make sure you check for the path to a 0 child node as well.
$$$O(n(log(max ai))^2)$$$ solution to E.
For what purpose there was this limitation in A, that "no character is contained in both strings."?
If smallest character in s equals to smallest character in t, which should we choose?
Sorry, I still dont get it, what is wrong with this submission 160146764 ?
160162775 check this
omg... thanks.
If you take a character from string a, you are not resetting the count for the other string to 0.
Assume given strings are a = "aaacdd" and b = "bcde", and k=10. Your vector ab will be then ["ddcaaa", "edcb"].
Initially, your cnt = [0,0] and ans is empty. After first three iterations, ans becomes "aaa", cnt = [3,0], and ab = ["ddc", "edcb"]. Now in fourth iteration, ans becomes "aaab" but cnt = [3,1]. It should become [0,1].
Can you please check my solution if that condition is not included: comment link
anyone plz discuss the approach of problem D. it will be very helpful for me, why it's maximize i+j and i-j, and , minimized i+j and i-j also.
you can see an atcoder's problem in there. The official editorial has a detailed explanation
Not figuring out definitely correct (strict $$$O(nm)$$$ complexity) solution for D, but use some tricks to get it passed.
It is plausible to assume that $$$ans$$$ is close to the "center" of black cells (here I adopt $$$center=\frac{max-min}{2}$$$ for both x and y axis), then iterate over and move to adjacent cells util max Manhattan distance descend to optimum.
I'm not sure if max Manhattan distance has the same property of monotonicity as Euclidean distance (a classical problem is covering points on the plane with smallest circle). If that property holds, binary search may also work.
Yeah, I also thought of binary search, but the precomputation had to be done of diamond shapes of size k. Please share if you come across any such resources of doing the same.
In problem C, can someone provide a smaller test case in which deleting the child with a higher subtree will lead to the wrong result? Thanks in advance!!
1
7
1 2
1 3
3 4
3 5
2 6
6 7
here root 1 : left child subtree (with root 2) has the same number of vertices that can be saved by
right child subtree(with root 3).
so if you cut left child subtree in the end answer will equal 2
but if you cut right child subtree in the end will equal 3
For same number of subtrees, I deleted the one with higher number of children
The tests for A are very weak. I can see many solution hackable. I can't see the hack button. But here is the test case:
if this works swap the strings
Example: https://codeforces.com/contest/1689/submission/160093968 :
UPDATE: Almost every solution is hackable. Why I can't see hack button?
Testcases are not weak. Read the problem A again :)
Hey, same symbol cannot appear in both strings a and b!
Ah sorry
Its wrong.
1689E - ANDfinity can be optimized to $$$O(n A^2)$$$, where $$$A=\log{\max a_i}$$$
We can count $$$cnt[i][j]$$$ how many times pair of bits $$$i,j$$$ was in all $$$a_k$$$ it's works in $$$O(A^2)$$$ per element and then check if this grpah connected
To check if bit set just check $$$a[i][i] > 0$$$, if we have array $$$cnt$$$ DFS works in $$$O(A^2)$$$
So when we adding or subtracting 1 we can just update cnt we are doing it $$$O(n)$$$ times
code: 160147889
Oh! Problem D had such simple solution. But I overkilled it with binary search.
Can you please explain how you used binary search I thought of doing so, searching for optimal distance but got dtucked on how to verify if the rhombus around all black points intersect at some pointfor current mid
There are four sides in rhombus. In all the cells of two opposite sides i + j remains the same and in all the cells in other two opposite sides i — j remains same where i and j are row and column number. So I divided them into two sets of ranges of two types where in first type, each range is of the form [i + j — mid, i + j + mid] and in other type, ranges are of form: [i — j — mid, i — j + mid]. Then just find the intersection of both type of ranges and iterate over every cell (i, j) to check if i + j lies in intersected range of first type of ranges and i — j lies in the intersected range of second type of ranges.
dang I was really close with D, but I wrongly thought that 4 squares shouldn't be sufficient and end up making convex hull
B was too googlable, it was simply "minimum derangement" but overall the contest was nice!
[DELETED]
Can someone explain D please. I don't understand what 4 regions is getting created
The regions are top-left rectangle, top-right rectangle, bottom-left rectangle and bottom-right rectangle, which are created by lines parallel with coordinate axes passing through our yellow point.
I'll add this in the editorial.
what does i+j, i-j signify can you explain it more?
in D, As per editorial, we are selecting 4 points with different cases. Now what if you find answer to a point which is not able to belong to the correct case. I mean case1 is for both positive but is not getting achieved. explain plz?
Please tell me why my BFS code is not working on Prob C.
Please use spoiler to write your code.
I mean this way
Prob A is not diffcult, but cost me 48 minutes to solve it, becaue I add multi characters to string c in one operation. o(╥﹏╥)o
Can someone tell me in 1689D - Lena and Matrix why taking average of leftmost and rightmost row and column (i.e. x=avg of(max row i+ min row i) and y=(max column j+ min column j) and taking all pssible value of (x,y) by taking ceil and floor value(i.e. 4 case) and checking which gives minimum distance for all black co0rdinates is giving wrong answer.(160145986). Any counter example to show this method is wrong??
I have a doubt the code given for A gives wrong answer for
1
6 4 2
aaaaaa
aaaa
given_answer:aaaaaaaa
expected:aaaaa
I was thinking that we should also consider whether string a is small or stering b at a moment when both has same smallest character. Please correct me.
you have to stop when any of the string is empty and since "a" is lexographically smaller than "aa" so its better to empty the second string first to get optimal string
yaa exactly but many submissions including the editorial one gives the wrong answer as answer should be aaaaa. Correct me plz
Actually in given question same character does not appear in both strings.
But lets say we allow same character to occur, then the answer in your case would be $$$aaaaaaaaa$$$ (9 times $$$a$$$)Oh okay got it forgot to read that.
Why the answer should be 9 times a we take 2 aa from string b then one a from string a and again 2 aa from string b. Now b is empty hence answer should be aaaaa.
But yaa I have to read the problem more carefully
Yes you are right here, lexicographically smaller string should be smaller!
The editorial's solution for problem D 1689D - Lena and Matrix may be too slow for languages like Python. I found a small speedup that allows Python code to pass the time limit.
Instead of "iterating over all squares in the matrix and finding the most distant black square", not all squares in the matrix actually need to be checked. For example, points outside the black diagonal rectangle (as shown in the editorial) clearly can't be optimal, and hence don't need to be checked.
Intuitively, points near the middle of the black diagonal rectangle have the best chance of being optimal and should be checked. I'm not sure how to prove that this is sufficient other than "Proof by AC" ;)
The time complexity is still O(nm) but maybe with a smaller constant factor.
Slow version, where all squares are checked (TLE in Python): https://codeforces.com/contest/1689/submission/160175658
Fast version, where only 4 middle squares are checked: https://codeforces.com/contest/1689/submission/160175205
A more complicated but mathematical(?) solution for D via direct analysis of manhattan distance.
First note that if any black square is between two other black squares in the same row or column then in the optimal configuration the longest distance will not be to that square. This can be shown by computing the manhattan distances to an arbitrary point directly. One of the squares on its left/right side will have greater distance. So removing those squares we have $$$O(n+m)$$$ black squares left.
Now fix some row $$$a.$$$ We find the optimal column(s) $$$b$$$ that minimize the distance for squares in this row. Thus, we want to minimize $$$\max ( |a-x_i| + |b-y_i| )$$$ for $$$b \in [1,m].$$$ Each of the $$$|a-x_i|$$$ are constants, so we have functions of the form $$$c + |x - d|.$$$ It's easy to see (by looking at the graphs) that the maximum of two such functions $$$\max(c_1 + |x - d_1|, c_2 + |x - d_2|)$$$ is another such function $$$c_3 + |x - d_3|.$$$ It follows that the function $$$f(b) = \max ( |a-x_i| + |b-y_i| )$$$ is bitonic, and we can binary search to find the optimal $$$b$$$ value(s) for this row.
Solution runs in $$$O(n^2 \log n)$$$ because for each of $$$n$$$ rows binary search takes $$$\log n$$$ and and each one we check we compute $$$O(n)$$$ numbers to find $$$f(b)$$$ at that column $$$b.$$$
163193116
not only can we binary search we can solve a system of equations to get exactly an x and y that will minimize the manhattan distance!
this is done by noting that the maximum distance for a number of points would be max( a-xi + b-yi, xi-a + b-yi, a-xi + yi-b, xi-a + yi-b ) where i is the ith black square
then we can see that we can compute the max manhattan distance is
max( a+b + max(-xi-yi),
to minimize the maximum manhattan distance would be the equivalent of solving
a+b + max(-xi-yi) = -b-a + max(xi+yi)
b-a + max(xi-yi) = a-b + max(-xi+yi)
though the problem with this is that a and b are not always integers
in my submission i checked the four nearest integer points ¯_(ツ)_/¯ couldn't think of a better solution
https://codeforces.com/contest/1689/submission/160184723
In D, we are checking 4 points. But for each point we are checking, there should be 4 cases for signs. What if the points we have chosen can only make 3 sign cases and cannot make the 4th sign case. Explain please.
Even if we have just one B all 4 cases will be covered.
I mean while checking for a certain white element, the black which we considered giving maximum or minimum for (let's say) case 3(+-) is not being in case 3 with the current white we are checking.
We take a black (2,3) with min i-j = -1 (case 3). When we are checking for white at (0,0) 0-2 = -2, 0-3 = -3, it belongs to case 4. So we should have chosen a different point which could have given a good case 3 with this point
Actually the solution is correct and maybe it requires some extra proof. That's what I am asking
Hehe finally got my O(nm + number of black points) solution for problem D to work :)
just in case of a harder problem in which n = 10e9, m = 10e9, and only the black points are given
https://codeforces.com/contest/1689/submission/160184723
Can anyone explain why the maximum answer can be 2 for E?
maximum 2 operations after all the 0s have been turned into 1s
for example
1000
0010
0010
=>
1000
1100
1000
the algorithm in general would be
find maximum ai & -ai and two numbers that ai & -ai = max(ai & -ai)
add 1 to one such number
minus 1 from another one such number
the minus 1 would become 11111110
the add one would become 10000001
since largest ai & -ai all other (ai & -ai) < max(ai & -ai) would be connected to 1111110
then 10000001 would connect to all ai & -ai == max(ai & -ai)
Got it. Thanks!!!
Can someone point out my mistake in C!? What I did is: At each level of BFS, I found the node with largest number of nodes in subtrees. Added that amount to result and continue BFS with rest nodes of that level. My Solution
Well, that does not work. The optimal solution is not to allways choose the bigger of the two subtrees. Instead, we have to choose the one where we can stop the infection at the earliest step. That is, where the path to the first vertex with less than two childs is shortest.
For 1st problem I tried a test case 1 5 5 2 aabbc aabbd The correct answer for this should be aaaabbbbc, but even their solution is giving aaaabbbbd. If someone is getting correct answer please check by reversing the string order and please correct me if a I am going wrong somewhere.
The question stated: no [same] character is contained in both strings.
Can we do D in O(K) where K denotes the number of black squares?
I think there is an $$$O(n$$$ $$$log(max(a_i))$$$ $$$+$$$ $$$log^2(max(a_i)))$$$ solution for problem E. Details is as follows:
First of all, the current solution can be sped up to $$$O(n$$$ $$$log^2(max(a_i)))$$$ by using dynamic connectivity or creating a spanning tree which connects all the nodes for every $$$a_i$$$, updating it for every $$$+1$$$ or $$$-1$$$ operation and running DSU to check if the bits are connected. That way, the precomputation part will be $$$O(n$$$ $$$log(max(a_i)))$$$, and the checking part can be done in $$$O(log^2(max(a_i)))$$$.
For the second optimization, I claim that only checking $$$log(max(a_i))$$$ times is sufficient for us to determine whether there exists a construction for answer $$$=$$$ $$$1$$$.
First of all, we have to precompute the connectivity of the 30 bits in the given configuration (after adding $$$1$$$ to every $$$a_i$$$ $$$=$$$ $$$0$$$) using DSU. Then, we store the index of the LSB (least significant bit) of every connected component in a set (which I'll call $$$R$$$). To check answer = $$$0$$$ we simply have to check if $$$|R|$$$ $$$=$$$ $$$1$$$.
Lemma 1: $$$+1$$$ operations only work if $$$|R|$$$ $$$=$$$ $$$2$$$ and $$$min(R_i)$$$ $$$=$$$ $$$0$$$.
Case 1: $$$a_i$$$ is even
Adding $$$1$$$ to $$$a_i$$$ means connecting the current component with the $$$0$$$th bit, which reduces the no. of components by at most $$$1$$$.
Case 2: $$$a_i$$$ is odd
Adding $$$1$$$ to $$$a_i$$$ means possibly disconnecting some parts of the current components, and connecting the current component with $$$1$$$ bit (can be any bit except for $$$0$$$). For this operation, the best case reduces the no. of components by $$$1$$$ as well, so $$$|R|$$$ $$$=$$$ $$$2$$$ must be true.
Furthermore, observe that the current component $$$a_i$$$ is in has the $$$0$$$th bit, which must be the LSB of the component. Therefore, we can add $$$1$$$ to an element from the other component instead and achieve the same result.
Lemma 2: $$$-1$$$ operations only work when LSB of current value $$$\geq$$$ $$$max(R_i)$$$ and the current component doesn't disconnect after the operation.
A $$$-1$$$ operation means removing an edge between the component and the LSB (hence possibly disconnecting them) and adding an edge between it and every bit less than the LSB.
We can prove this lemma by contradiction. Assume there exists a $$$-1$$$ operation on an element $$$a_i$$$ with LSB $$$<$$$ $$$max(R_i)$$$. Obviously, that element won't be in the component $$$max(R_i)$$$, and after the $$$-1$$$ operation, it still won't be connected with that component as all the bits affected aren't in that component. Therefore, it won't be possible if the LSB of the current value $$$<$$$ $$$max(R_i)$$$.
Even if some $$$a_i$$$ satisfies the first condition, the component $$$a_i$$$ is currently in might disconnect after performing the operation, so we have to check whether the component is connected using the $$$O(log^2(max(a_i)))$$$ checking method above.
(Side note: There might be some faster methods for checking as we only have to check whether a component is disconnected or not. If you have any ideas, please comment below!)
Lemma 3: We will find a solution after checking at most $$$log(max(a_i))$$$ distinct values that has LSB $$$\geq$$$ $$$max(R_i)$$$.
Notice that in order for a component to disconnect after the $$$-1$$$ operation, the edge that was removed must be a bridge in the graph. In a graph, there will be at most $$$n-1$$$ bridges, where $$$n$$$ is the number of nodes. Therefore, in our graph, there will be at most $$$log(max(a_i)) - 1$$$ bridges, and we will find a valid configuration after at most $$$log(max(a_i))$$$ tries.
Note that for values with a single bit (a perfect power of 2), only $$$a_i$$$ $$$=$$$ $$$2^{LSB}$$$ might not be valid, and the rest must be valid.
Hence, we can find the answer with overall time complexity $$$O(n$$$ $$$log(max(a_i))$$$ $$$+$$$ $$$log^2(max(a_i)))$$$. The $$$O(n$$$ $$$log(max(a_i)))$$$ is from the precomputation for the graph, and $$$O(log^2(max(a_i)))$$$ is for the queries.
Here is my implementation of the above solution. If you spot any flaws in my solution, please comment below; I would very much appreciate it. Also, sorry for my bad English ._.
Problem C can be solved using a simple preorder traversal, with only an adjacency list as extra memory. Essentially:
If the current node has no children, then the infection has reached it's end, and the current killed node count can be compared to the global
min_killcount.If the current node has one child, it can be stopped by pruning that one child. This ends the infection, and increases the kill count by 1 extra, so we compare
current_kill+1instead.If the current node has 2 children, we will try pruning each child. This causes the child to die, and the other node to be infected, so dfs is called again with
current_kill+2.This strategy will explore every path that the infection can take and store the minimum killed nodes in a single variable.
I tried the approach of Manhattan distance and rotating technique for problem D.Many people have solved this problem by DP. Can any one please explain your DP appraoch?
Thank you in advance for helping.
n0sk1ll, How to prove the solution for B?
Is there rigorous proof for question D?
Go to CSES book -> Advanced Topics -> Geometry -> Distance Functions -> Rotating co-ordinates
I have some questions about the solution to problem A. What if I have taken all the characters in string A but there is still more than k characters in string B?
For problem E, there exists easier way to check if graph is connected.
Repeat $$$log$$$ $$$max$$$ $$$a_i$$$ times following :
Finally if there exists some $$$a_i$$$ that $$$a_i$$$ $$$\text&$$$ $$$a_0=0$$$ then graph is disconnected.
In problem E, the check for connectivity can be done in $$$O(n \log{max(b_i)})$$$ in another way too:
Construct bipartite graph with one set of nodes corresponding to elements of the array, and one set of nodes corresponding to bits, edge exists between element $$$i$$$ and bit $$$x$$$ if $$$x$$$'th bit is set in $$$a_i$$$. Finally, just check this constructed graph.
In D you can just rotate co-ordinates in 45 Degress that makes stuff really easy
Do you know why is taking leftmost, rightmost, top-most and bottom-most black points and taking their middle (4 ways at max) and then finding which one them gives minimum answer results in WA ?
because in each of them you are considering either x or y never both of them
Oh so you mean if we take that condition, there might be some cases where the sum of x,y will be greater than the condition we imposed since the conditions are independent on x and y whereas the one mentioned in editorial takes both x,y into account. Am I right in understanding ?
Thanks for the help.
yes
Testcases for A are weak. https://codeforces.com/contest/1689/submission/238293004 In this submission the output for 1 2 1 2 ab a The output of code-aa Actual output-a I'm not sure if the testcases can be changed now but just noticed the error so thought I should comment it.