384A - Кодер
Usually, when you don’t have any idea how to approach a problem, a good try is to take some small examples.
So let’s see how it looks for N = 1, 2, 3, 4 and 5. With C I noted the coder and with * I noted an empty cell.
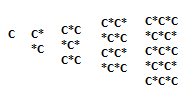
By now you should note that answer is N ^ 2 / 2 when N is even and (N ^ 2 + 1) / 2 when N is odd. Good. Generally, after you find a possible solution by taking examples, you need to prove it, then you can code it.
In order to proof it, one needs to do following steps:
1/ prove you can always build a solution having N ^ 2 / 2 (or (N ^ 2 + 1) / 2) pieces.
2/ prove that N ^ 2 / 2 (or (N ^ 2 + 1) / 2) is maximal number – no other bigger solution can be obtained.
For proof 1/ imagine you do coloring like in a chess table.

The key observation is that by placing all coders on black squares of table, no two coders will attack. Why? Because a piece placed at a black square can attack only a piece placed at a white square. Again, why? Suppose chess table is 1-based. Then, a square (i, j) is black if and only if i + j is even. A piece placed at (i, j) can attack (i + 1, j), (i – 1, j) (i, j + 1) or (i, j – 1). The sum of those cells is i + j + 1 or i + j – 1. But since i + j is even, i + j + 1 and i + j – 1 are odd, hence white cells.
Depending on parity of N, number of black cells is either N ^ 2 / 2 or (N ^ 2 + 1) / 2. For N even, one can observe that there are equal amount of black and white cells. Total number of cells is N ^ 2, so number of black cells is N ^ 2 / 2. For N odd, number of black cells is number of white cells + 1. We can imaginary add a white cell to the board. Now, number of black cells will be also equal to number of white cells, so answer is (N ^ 2 + 1) / 2.
2/ Two coders attack each other if they are placed at two adjacent cells, one black and other one white. One needs to prove that adding more than number from 1/ will cause this to happen. If you place a coder at a white cell, you won’t be able to place at least one coder at a black cell, so in best case you don’t win anything by doing this. Hence, it’s optimally to place all coders on same color cells. Since cells colored in black are always more or equal to white ones, it’s always optimally to choose black color. But number from 1/ is the number of cells having black color. Adding one more piece will force you to add it to a white color cell. Now, you’ll have a piece placed at a black colored cell and one placed at an adjacent white colored cell, so two coders will attack. Hence, we can’t place more than number from 1/ pieces.
Code: http://pastie.org/8651801
384B - Мультизадачность
Let’s start by saying when array A[] is sorted:
1/ is sorted in ascending order when i < j and A[i] <= A[j]. It is NOT sorted when i < j and A[i] > A[j].
2/ is sorted in descending order when i > j and A[i] <= A[j]. It is NOT sorted when i > j and A[i] > A[j].
Iahub can choose 2 indices i, j and swap values when A[i] > A[j]. If A[i] <= A[j], he’ll ignore operation. Hence, if he wants to sort all arrays in ascending order, he chooses indices i, j when i < j and perform operation. Otherwise, in all his operations he uses indices i, j such as i > j. A “good” operation is when choosing indices i < j for ascending order sorting and i > j for descending order sorting. By doing only good operations, after an array is sorted, it will stay sorted forever (for a sorted array, all good operations will be ignored).
From here we get our first idea: use any sorting algorithm you know and sort each array individually. When print swaps done by sorting algorithm chosen, print them as good operations. However, sorting each array individually can cause exceeding M * (M — 1) / 2 operations limit. Another possible solution would be, after you did an operation to an array, to update the operation to all arrays (you printed it, so it counts to M * (M — 1) / 2 operations limit; making it to all arrays will help sometimes and in worst case it won’t change anything). However, you need to code it very careful in order to make this algorithm pass the time limit. Doing this in a contest is not the best idea, especially when implementation could be complicated and you have no guarantee it will pass time limit.
So what else can we do? We can think out of box. Instead of sorting specific N arrays, you can sort all possible arrays of length M. Find a sequence of good operations such as, anyhow I’d choose an array of size M, it will get sorted ascending / descending.
I’ll show firstly how to do for ascending sorting. At position 1 it needs to be minimal element. Can we bring minimal element there using good operations? Yes. Just do “1 2” “1 3” “1 4” ... “1 M”. It basically compares element from position 1 to any other element from array. When other element has smaller value, swap is done. After comparing with all M elements, minimal value will be at position 1. By now on I’ll ignore position 1 and move to position 2. Suppose array starts from position 2. It also needs minimal value from array, except value from position 1 (which is no longer in array). Hence doing “2 3” “2 4” “2 5” ... “2 M” is enough, by similar reasons. For a position i, I need minimal value from array, except positions 1, 2, ..., i – 1. I simply do “i i+1” “i i+2” ... “i M-1” “i M”. By arriving at position i, array will be sorted ascending. The algorithm is simply:
for (int i = 1; i < M; ++i)
for (int j = i + 1; j <= M; ++j)
cout << i << “ “ << j << “\n”;
This algorithm does exactly M * (M — 1) / 2 moves.
Can you find out how to sort array in descending order? Try to think yourself, then if you don’t get it read next. At first position of a descending array it needs to be maximal value. Similarly to ascending order, we can do “2 1” “3 1” “4 1” ... “M 1”. When I’m at a position i and I compare its value to value from position 1, doing operation “i 1” checks if A[i] > A[1]. If so, it swaps A[i] and A[1], so position 1 will contain now the maximum value so far. Similarly to logic from ascending order, when I’m at position i, I need maximum value from array except positions 1, 2, ..., i – 1, so I do “i+1 i” “i+2 i” ... “M i”. Algorithm is:
for (int i = 1; i < M; ++i)
for (int j = i + 1; j <= M; ++j)
cout << j << “ “ << i << “\n”;
Obviously, this does as well M * (M — 1) / 2 operations worst case. All algorithm is about 10 lines of code, much better than other solution, which requires two manually sorts and also has a chance to exceed TL.
Code: http://pastie.org/8651809
384C - Доим коров
A good strategy to approach this problem is to think how optimal ordering should look like. For this, let’s calculate for each 2 different cows i and j if cow i needs to be milked before or after cow j. As we’ll show, having this information will be enough to build optimal ordering. It is enough to consider only cases when i < j, case when i > j is exactly the opposite of case i < j. For formality, I’ll call the optimal ordering permutation and lost milk the cost of permutation.
So, for an optimal permutation P let’s take 2 numbers i < j and see in which cases i should appear before j in permutation (i is before j if P[pos1] = i, P[pos2] = j and pos1 < pos2; otherwise we’ll call i is after j). We have 4 possible cases:
1/ A[i] = 0 and A[j] = 0
If we put i before j, no additional cost will be added. Since j is in right of i and i only adds cost when it finds elements in left of i, j won’t be affected when processing i. When processing j, i will be already deleted so it won’t affect the cost either. Hence, we can put i before j and no cost will be added.
2/ A[i] = 0 and A[j] = 1
Here, i and j can appear in arbitrary order in permutation (i can be before or after j). No matter how we choose them, they won’t affect each other and cost will remain the same.
3/ A[i] = 1 and A[j] = 0
As well, here i and j can appear in arbitrary order. If we choose i first, j will be in right of it, so cost of permutation will increase by one. If we choose j first, i will be in left of it so cost of permutation will increase as well. No matter what we do, in this case cost of permutation increases by 1.
4/ A[i] = 1 and A[j] = 1
Here, i needs to be after j. This adds 0 cost. Taking i before j will add 1 cost to permutation (since j is in right of i).
Those 4 cases show us how a minimal cost permutation should look. In a permutation like this, only case 3/ contributes to final cost, so we need to count number of indices i, j such as i < j and A[i] = 1 and A[j] = 0 (*). If we show a permutation following all rules exists, task reduces to (*).
By cases 2/ and 3/ it follows that in an optimal permutation, it only matters order of elements having same value in A[]. We can put firstly all elements having value 0 in A[], then all elements having value 1 in A[]. We can order elements having value 0 by case 1/ and elements having value 1 by case 4/. More exactly, suppose i1 < i2 < ... < im and (A[i1] = A[i2] = ... = A[im] = 0) and j1 > j2 > ... > jn (A[j1] = A[j2] = ... = A[jn] = 1). Then, a permutation following all rules is {i1, i2, ..., im, j1, j2, ..., jn}. This permutation can always be built.
Hence, task reduces to (*): count number of indices i, j such as i < j and A[i] = 1 and A[j] = 0. We can achieve easily an O(N) algorithm to do this. Let’s build an array cnt[j] = number of 0s in range {j, j + 1, ..., N} from array A. We can easily implement it by going backwards from N to 1. The result is sum of cnt[i], when A[i] = 1.
Code: http://pastie.org/8651813
384D - Вулканы
Our first observation is that if there is a path from (1, 1) to (N, N), then the length of path is 2 * N – 2. Since all paths have length 2 * N – 2, it follows that if there is at least one path, the answer is 2 * N – 2 and if there isn’t, the answer is -1. How to prove it? Every path from (1, 1) to (N, N) has exactly N – 1 down directions and exactly N – 1 right directions. So, total length for each path is N – 1 + N – 1 = 2 * N – 2.
So we reduced our problem to determine if there is at least one path from (1, 1) to (N, N). This is the challenging part of this task, considering that N <= 10 ^ 9. How would you do it for a decently small N, let’s say N <= 10^3 . One possible approach would be, for each row, keep a set of reachable columns. We could easily solve this one by doing this: if (i, j) denotes element from ith row and jth column, then (i, j) is (is not) reachable if:
if (i, j) contains a volcano, then (i, j) is not reachable. Otherwise, if at least one of (i – 1, j) and (i, j – 1) is reachable, then (i, j) is reachable. Otherwise, (i, j) is not reachable.
What’s the main problem of this approach? It needs to keep track of 10^9 lines and in worst case, each of those lines can have 10^9 reachable elements. So, worst case we need 10^9 * 10^9 = 10^18 operations and memory.
Can we optimize it? We can note for beginning that we don’t need to keep track of 10^9 lines, only m lines are really necessarily. We need only lines containing at least one obstacle (in worst case when each line contains only one obstacle, we need m lines). How to solve it this way? Suppose line number x contains some obstacles and lines x + 1, x + 2, x + 3 do not contain any obstacle. Suppose we calculated set S = {y | cell (x, y) is reachable}. How would look S1, S2, S3 corresponding to lines x + 1, x + 2, x + 3? For S1, we can reach cell (x + 1, ymin), where ymin is minimal value from set S. Then, we can also reach {ymin + 1, ymin + 2, ..., N}, by moving right from (x + 1, ymin). So S1 = {ymin, ymin + 1, ..., N}. How do S2 and S3 look? It’s easy to see that they’ll be as well {ymin, ymin + 1, ..., N}. So we get following optimization: suppose set of lines containing at least one obstacle is {L1, L2, ..., Lk}. We need to run algorithm only for lines L1, L1 + 1, L2, L2 + 1, L3, L3 + 1, ..., Lk, Lk + 1.
It looks like we didn’t make anything with this optimization. Even if we calculate for m lines, each line can still have 10^9 reachable positions. So worst case we perform 10^14 operations. We need something better for managing information from a line. You can note that for a given line y, there are a lot of positions having consecutive values. There are a lot of positions (x, y) and (x, y + 1) both reachable. This should give us following idea: what if instead of keeping reachable positions, we keep reachable ranges? That is, for each line x we keep a set of ranges S = {(a, b) | all cells (x, k) with a <= k <= b are reachable}.
How many ranges can it be for a line? If the line contains m obstacles, there are m + 1 ranges. Suppose for line x all cells are reachable, but for line x + 1 cells (x + 1, 3) (x + 1, 5) (x + 1, N – 1) are blocked. Then, the ranges of reachable cells are [1, 2] [4, 4], [6, N – 2] and [N, N]. By now, we get worst case m lines and worst case each line having m elements, so in worst case we’d have to handle m * m = 10 ^ 10 events. This may still look too much, but happily this bound is over estimated. If a line has o obstacles, there can be at most o + 1 ranges. If lines L1, L2, ..., Lk have {o1, o2, ..., ok} obstacles, there’ll be at most o1 + o2 + ... + ok + k ranges. But o1 + o2 + ... + ok = m and also k is at most m (proved above why we’re interested in at most m lines), so in worst case we get m + m = 2 * m ranges. Yaay, finally a decent number of states for this problem :)
So, we iterate each line we’re interested in. Let’s find set of ranges for this line, thinking that all cells from line above are reachable. This is easy to do. After we get our ranges like all cells from above can be visited, let’s think how having obstacles above can influence current ranges. After adding ranges from above, current ranges can’t increase (obviously), they can only decrease, remain the same or some of them can become empty. So, let’s take each range [a, b] from current line and see how it will transform after adding ranges from previous line.
Given range [a, b], it can transform only in [a’ , b] with a’ >= a. If a’ > b, then obviously range is empty. Why second number of range keeps constant? Let a’ smallest reachable column from current line which is in range [a, b]. It’s enough to check a’ >= a, as if a’ > b, range will be empty. It’s obviously why we need to keep a’ smallest value possible >= a: we’re interested to keep range as big as possible and as less as we cut from left, as big it is. Once we’ve found a’ in range [a, b] (or a’ > b if range is empty) all cells {a’ + 1, a’ + 2, ..., b} are reachable as well by going right from a’, so if interval is not empty, then second number defining it remains b.
Next question is how to find a’ fast enough. In order a point a’ to be reachable on current range, it also needs to exist a range on previous line containing it. If the range from previous line is [pa, pb] then a’ needs to follow 3 conditions:
a’ minimal such as
pa <= a’ <= pb
a’ >= a
What if instead of finding a’ we find [pa, pb]? Then a’ is max(pa, a). In order a’ to be as small as possible, since a is constant, pa needs to be as small as possible. So we reduced it to:
pa minimal pb >= a’ >= a <=> pb >= a
Intervals from previous line are disjoint, no 2 intervals cross each other. It means that if pb is minimal, than pa is minimal too (if we increase pb, then pa will increase too, so it won’t be minimal). Hence, you need to find an interval [pa, pb] such as pb is minimal and pb >= a. Then, a’ is max(a, pa). This is easy to do if we sort all intervals from previous line increasing by second value (pb), then we binary search for value a.
Finally, after running algorithm for all lines, last range from last line has second number N (assuming ranges are sorted increasing by second value), then there exist a path, otherwise there does not exist. This algorithm should run O(m * logm) worst case, good enough to pass.
Code: http://pastie.org/8651817
384E - Дерево подвижных сумм
This is kind of task that needs to be break into smaller subproblems that you can solve independently, then put them together and get solution.
Let’s define level of a node the number of edges in the path from root to the node. Root (node 1) is at level 0, sons of root are at level 1, sons of sons of root are at level 2 and so on.
Now suppose you want to do an operation of type 1 to a node x. What nodes from subtree of x will be added +val (a positive value)? Obviously, x will be first, being located at level L. Sons of x, located at level L + 1 will be added –val. Sons of sons, located at level L + 2, will be added value +val again. So, nodes from subtree of x located at levels L, L + 2, L + 4, ... will be added a +val, and nodes located at levels L + 1, L + 3, L + 5 will be added a –val. Let’s take those values of L modulo 2. All nodes having remainder L modulo 2 will be added a +val, and nodes having reminder (L + 1) modulo 2 will be added –val. In other words, for a fixed x, at a level L, let y a node from subtree of x, at level L2. If L and L2 have same parity, +val will be added to y. Otherwise, -val will be added to y.
From here we have the idea to split nodes of tree in 2 sets – those being located at even level and those being located at odd level. What still makes the problem hard to solve? The fact that we have a tree. If nodes from a subtree would be a contiguous sequence instead of some nodes from a tree, problem would be simpler: the problem would reduce to add / subtract values to all elements of a subarray and query about a current value of an element of array. So, how can we transform tree to an array, such as for a node x, all nodes from subtree of x to be a subarray of array?
The answer is yes. We can do this by properties of DFS search. Before reading on, make sure that you know what is discovery time and finish time in a DFS search. Let’s build 3 arrays now – discover[], representing nodes in order of their discover times (a node is as before in discover as it has a small discover time), begin[] = for a node, in which time it was discovered and end[] = what’s last time of a discovered node before this node finishes. For a subtree of x, all nodes in the subtree are nodes in discover from position begin[x] to end[x].
Example: suppose you have tree 1-5; 1-6; 6-7; 6-4; 4-2; 4-3
Discover is {1, 5, 6, 7, 4, 2, 3}.
begin is {1, 6, 7, 5, 2, 3, 4}.
end is {7, 6, 7, 7, 2, 7, 4}.
What’s subtree of node 6? elements of discover from position begin[6] to end[6]. In this case, from 3 to 7, so elements {6, 7, 4, 2, 3}. You can see it’s correct and take more examples if you want :)
Now, we reduced problem to: you’re given an array A. you can perform 2 operations:
1/ increase all elements from a range [x, y] to a value val (val can be negative, to treat subtractions)
2/ what’s current value of an element from position pos.
Those who solved “Iahub and Xors” from my last round, CF 198, should probably say they saw something similar before. If you didn’t solve problem before, I encourage you to do it after you solve this one, it uses a similar idea to what will follow now. Also, if you don’t know Fenwick trees, please read them before moving on. An alternative would be for this task using segment trees with lazy update, but I see this one more complicated than needed.
I’ll use now a not so common approach when dealing with data structures. Instead of keeping in a node the result, like you usually do, I’ll keep just an auxiliary information. So what algorithm proposed does:
Let A an array, initially with all elements 0.
When you need to update range [x, y] with value val, you simply do A[x] += val and A[y + 1] -= val.
When you need to answer a query about position pos, you output A[1] + A[2] + ... + A[pos].
Implemented brute force, you get O(1) per update and O(N) per query. However, these both are operations supported by a Fenwick tree, so you can get O(logN) per operation.
It may not be very clear why this algorithm works. Let’s take a closer look: an update needs to add value val only to range [x, y]. When you query a position pos, let’s see if algorithm handles it correctly:
1/ pos < x. In this case, result must not be affected by my update. Since pos < x and I only updated 2 values with indices >= x, when doing A[1] + A[2] + ... + A[pos] it won’t matter at all I did that update – at least not for this query.
2/ x <= pos <= y. Here, for a pos, I need to add value val only once. We add it only at A[x] – in this way it will be counted once, and it will be considered for each elements from range [x, y] (since an element at position p from range [x, y] has p >= x, in A[1] + A[2] + ... + A[p] I’ll have to consider A[x]).
3/ pos > y. Here I don’t have to consider the query. But it would be considered when processing A[x]. But if I add to A[y + 1] value –val I’ll just cancel the value previously added.
Code (actually we use just one Fenwick tree instead of 2, can you think why it works? :) ) : http://pastie.org/8651824
383D - Антиматерия
Author's solution
The problem is: given an array, iterate all possible subarrays (all possible elements such as their indexes are consecutive). Now, for a fixed subarray we need to know in how many ways we can color its elements in black and white, such as sum of black elements is equal to sum of white elements. The result is sum of this number, for each subarray.
Let’s solve an easier problem first. This won’t immediately solve the harder version, but it will be useful later. Suppose you’ve fixed a subarray. In how many ways can you color it with black and white? Suppose subarray has N elements and sum of them is M. Also, suppose for a coloring, sum of blacks is sB and sum of whites is sW. For coloring to be valid, sB = sW. But we also know that sB + sW = M (because each element is colored by exactly one color). We get that 2 * sB = M, so sB = M / 2. The problem is now: in how many ways can we color elements in black such as sum of blacks is M / 2 (after we fix a black coloring, we color with white non colored elements; sum of white colored elements is also M / 2). This is a well known problem: Knapsack problem. Let ways[i][j] = in how many ways one can obtain sum j from first i elements. When adding (i + 1) object, after ways[i] is calculated, for a fixed sum j we can do 2 things: add (i + 1) object to sum j or skip it. Depending of what we chosen, we add value ways[i][j] to ways[i + 1][j + value[i + 1]] or to ways[i + 1][j]. The result is in ways[N][M / 2]. This works in O(N * M) time.
An immediate solution can be obtained now: take all subarrays and apply above approach. This leads to an O(N ^ 2 * M ^ 2) solution, which is too much. One can reduce complexity to O(N ^ 2* M) by noting that processing subarray [i, j] can be done with already calculated values for subarray [i, j – 1]. Hence, instead of adding N elements, it’s enough to add 1 element to already calculated values (element from position j). Sadly, O(N ^ 2 * M) is still too slow, so we need to find something better. The solution presented below will look forced if you didn’t solve some problems with this technique before. It’s hard to come with an approach without practicing this kind of tasks. But don’t worry, as much as you practice them, as easily you’ll solve those problems.
We’ll solve task by divide and conquer. Complexity of this solution is O(N * M * logN). Let f(left, right) a function that counts number of colorings for each subarray [i, j], such as subarray [i, j] is included in subarray [left, right] (left <= i <= j <= right). Answer is in f(1, N). The trick is to define a value med = (left + right) / 2 (very frequent trick in divide and conquer problems, called usually a median). We can next classify [i, j] subarrays in 3 types:
1/ i <= med j <= med
2/ i > med j > med
3/ i <= med j > med
We can solve 1/ and 2/ by calling f(left, med) and f(med + 1, right). The remained problem is when i <= med and j > med. If we solve 3/ in O((right – left) * M) time, this will be enough to overall achieve O(N * M * logN) (for this moment trust me, you’ll see later why it’s so :) ).
Let’s denote by i1 last i1 elements from subarray [left, med]. Also, let’s note by i2 first i2 elements from subarray [med + 1, right]. For example, let left = 1 and right = 5, with array {1, 2, 3, 4, 5}. med is 3 and for i1 = 2 and i2 = 1, “left” subarray is {2, 3} and “right” subarray is {4}. By iterating i1 from 1 to med – left + 1 and i2 from 1 to right – med and then unite subarrays i1 and i2, we obtain all subarrays described in 3/ . Let’s denote by j1 sum of a possible black coloring of i1. Similarly, j2 is sum of a possible black coloring of i2.
Suppose we fixed i1, i2, j1 and j2. When it’s the coloring valid? Let S sum of united subarrays i1 and i2 (S = value[med – i1 + 1] + value[med – i1 + 2] + ... + value[med] + value[med + 1] + ... + value[med + i2 – 1] + value[med + i2]). Now it’s time to use what I explained at the beginning of solution. The coloring is good only when j1 + j2 = S / 2. We can rewrite the relation as 2 * (j1 + j2) = sum_of_elements_from_i1 + sum_of_elements_from_i2. We can rewrite it even more:
2 * j1 + 2 * j2 — sum_of_elements_from_i1 — sum_of_elements_from_i2 = 0
2 * j1 – sum_of_elements_from_i1 = sum_of_elements_from_i2 – 2 * j2 = combination_value
This relation is the key of solving problem. You can see now that relation is independent in “left” and “right” side. We calculate left[i1][j1] and right[i2][j2] = in how many ways can I obtain sum of blacks j1 (j2) from first i1 (i2) from left (right) side. Let’s calculate also count[value] = in how many ways can I obtain combination_value equal to value in the right side. For some fixed (i2, j2) I add to count[sum_of_elements_from_i2 – 2 * j2] value right[i2][j2]. In this way count[] is calculated correctly and completely. Now, let’s fix a sum (i1, j1) in the left side. We’re interested how many good colorings are such as there exist a coloring of j1 in i1 elements (the endpoint of “left” is fixed to be i1 and I need to calculate endpoints i2 for right, then to make colorings of i2). A coloring is good if combination_value of (i1, j1) and (i2, j2) is equal. Hence, I need to know in how many ways I can color i1 elements to obtain sum j1 and also I need to know in how many ways I can color elements from right to obtain same combination_value as it’s in the left. It’s not hard to see that answer for a fixed (i1, j1) is left[i1][j1] * count[2 * j1 – sum_of_elements_from_i1]. This takes O((right – left) * M) time.
The only thing remained in the problem is to see why complexity is O(N * M * logN). We can assume N is a power of 2 (it not, let’s round N to smallest power of 2 bigger than N; complexity for N is at least as good as complexity for this number). Draw a binary complete tree with N nodes. Each node corresponds to an appeal of f(). For a level, exactly O(N * M) operations are performed. To see why:
For level 1, there’ll be 1 node performing N * M operations.
For level 2, there’ll be 2 nodes performing (N / 2) * M operations. Summing up we get O(N * M).
For level 3, there’ll be 4 nodes performing (N / 4) * M operations. Summing up we get O(N *M) as well.
and so on.
So for each level we perform O(N * M) operations. A binary complete tree has maximum O(logN) levels, so overall complexity is O(N * M * logN).
Code: http://pastie.org/8651826
Solution fount by contestants
This was totally unexpected to us :) Good job finding it, you guys are really smart.
We observe that x units of antimatter is the same thing as -x units of matter. Then we can consider that an element produces either x or -x units of matter. A valid substring is one that can have the sum of the elements 0. The problem is reduced to finding how many different substrings can we have with sum 0 (a substring is different than another one if it has different indices, or if at least one element produces matter in one and antimatter in the other).
This problem can be solved with dynamic programming. We will hold D[i][j] = the number of substrings that end in element i, and have sum j. It's easy to see that D[i + 1][j] = D[i][j — x] + D[i][j + x], where x is the value of the current element (we can put either -x or x). After we finish computing all the values for current i, we add to the solution D[i][0] (how many valid substrings do we have). After that, we add 1 to D[i][0], meaning that there is an empty substring starting at position i (however, we don't need to add it to the answer).
For a code, check passing submissions during contest.
383E - Гласные
Author's solution
Let's iterate over all possible vowel sets. For a given set {x1, x2, ..., xk} we're interested in number of correct words from dictionary. After a precalculation, we can do it in O(k).
Suppose our current vowel set is {x1, x2, ..., xk}. How many words are covered by the current vowels? By definition, we say a word is covered by a set of vowels if at least one of 3 letters of word is in vowel set. We can calculate this number using principle of inclusion and exclusion. We’ll denote by |v1, v2, v3, ...| = number of words containing ALL of vowels v1, v2, v3, ... . Using principle of inclusion and exclusion we get:
number_of_words_covered = |x1| + |x2| + .. + |xk| — |x1, x2| — |x1, x3| — .... + |x1, x2, x3| + |x1, x2, x4| + .... + |xk-2, xk-1, xk|. This formula is simply a reformulation of principle of inclusion and exclusion. You can easily observe that |v1, v2, ..., vk| makes sense only when k is at most 3, as no word from input can contain 4 or more letters (and hence can’t contain 4 or more vowels).
Example:
Suppose words are abc, abd and bcd.
|a| = 2 (first 2 words both contain character a).
|a, b| = 2 (as well, first 2 words contain characters a and b).
|b| = 3 (all 3 words contain character b).
|a, b, d| = 1 (only second word contains all 3 characters).
Also, note how principle of inclusion and exclusion works. number of words covered for vowels {a, b} is |a| + |b| — |a, b| = 2 + 3 – 2. Indeed, answer is 3.
We divide our problem in 3 subproblems. First one, for a vowel set, compute sum of |a|, where a is a letter from subset. Second, compute sum of |a, b|, where both a and b are letters from set. Third, compute sum of |a, b, c|, where a, b, c are letters from set. As stated, the answer is number_from_1st_step + number_from_3rd_step – number_from_2nd_step. If you followed me, you’ll see that we want to compute results for each subproblem in O(queryLetters).
First subproblem can be solved trivially in O(queryLetters). Let array single[], with following meaning: single[c] is how many words contain character c. It can be trivially precomputed in O(24 * N). Note that if a word contains twice/third times a character c, it needs to be counted only one (e.g. word aba will add only 1 to single[a]). For compute result of this subproblem for a given set of vowels, I’ll take all letters from set. If letter belongs to set, I add to result single[letter]. This step can be also be solved in O(1), but there’s no need, since other subproblems allow only an O(queryLetters) solution.
For second and third subproblems it’s a little more difficult. I’ll present here how to solve second subproblem and some hints for third one (if you understand second, with hints you should be able to solve third one by your own).
Similarly to first step, I’ll define a matrix double[c1][c2] = how many words contain both characters c1 and c2. A trivially solution would be, for a given vowel set, take all combinations of letters c1 and c2 that belong to set and add to result value double[c1][c2]. However, this solves each query in O(queryLetters^2), which is too slow.
Note, if we’d have 12 letters, instead of 24, this approach would be fast enough. From here it comes a pretty classical idea in exponential optimization: meet in the middle attack. We split those 24 letters in 2 groups: first 12 letters and last 12 letters. The answer for a subset is sum of double[c1][c2] (when c1 and c2 belong to current vowel set) when
1/ c1 and c2 belong to first 12 letters
2/ c1 and c2 belong to last 12 letters
3/ c1 belongs to first 12 letters and c2 belongs to last 12 letters
1/ and 2/ can be immediately precalculated as stated above, in O(2 ^ 12 * 12 ^ 2). We’ll remember results for each half using bitmasks arrays. Let Half1[mask] = sum over double[c1][c2], when c1 and c2 are in first 12 letters and correspond to 1 bits of mask. Half2[mask] is defined similarly, but for last 12 letters (e.g. subset {a, c, d} corresponds to bitmask 2^0 + 2^2 + 2^3 = 13 in first half and subset {m, n, p} corresponds to bitmask 2^0 + 2^1 + 2^3 = 11 for second half). Now, for a given subset, one can answer first 2 parts in O(queryCount) worst case (read input for a query and convert it to bitmasks).
How to answer 3? With another precalculation, of course. We know c1 letter needs to be in first 12 letters and c2 needs to be in last 12 letters. The precalculation we do here is: mixed_half[mask][i] = sum over |c1, c2|, when c1 belongs to first half and is a 1 bit of mask and c2 is i-th character of second half. Hence, for a query, we can fix character from second half (c2, by iteration of query letters from second half) and know sums of |c1, c2| between it and all available characters from first half after we do this precalculation. Also, precalculation is done trivially in O(2 ^ 12 * 12^2): fix mask, fix i and then iterate over 1 bits from mask and add double[c1][c2].
Third subproblem is left, but it can be done similarly to second one. Instead of double[c1][c2], we’ll have triple[c1][c2][c3] = how many words contain all 3 characters c1, c2 and c3? We also do meet in the middle here, divide those 24 letters into 2 sets of 12 letters. We have 4 cases:
1/ c1, c2, c3 belong to first half
2/ c1, c2, c3 belong to second half
3/ c1, c2 belong to first half and c3 to second half
4/ c1 belongs to first half and c2, c3 to second half
1/ and 2/ are done brute force, like in second subproblem (the only difference is we choose 3 characters instead of 2, having complexity O(2 ^ 12 * 12 ^ 3)). For 3/ and 4/ we also precompute 2 matrixes:
mixed_two_one[mask][i] = c1 and c2 belong to mask from first half and c3 is i-th character from second half
and
mixed_one_two[mask][i] = c1 is i-th character from first half and c2, c3 belong to mask from second half.
Those can also be calculated in O(2 ^ 12 * 12^3).
So precalculation part is O(2 ^ 12 * 12 ^ 3) = 7077888 operations.
For calculate answering queries complexity, take all numbers from 0 to 2^24 — 1 and sum their bit count. This is a well known problem, the sum is 0 * C(24, 0) + 1 * C(24, 1) + ... + 24 * C(24, 24) = 201326592. In total we get 208404480 operations. C++ source makes them in 2 seconds.
Code: http://pastie.org/8651829
Solution fount by contestants
Like in D1 D task, official solution was over complicated. This solution is more simple to understand, code and it's more elegant. If someone wants to complicate his life, (s)he can code also official solution :)
Let's start by assigning a bitmask to each word in following way: ith bit is 1 if and only if letter ('a' + i) appears in the current word. For example, for word acd, its bitmask is 2^0 + 2^2 + 2 ^ 3 = 13 and for word aab its bitmask is 2^0 + 2^1 = 3. After reading the words from dictionary, we store a matrix cnt[mask] = how many words from dictionary correspond to mask?
We iterate bitmasks from 0 to 2^24 — 1, this time corresponding to each possible question of Iahubina. Let's focus on a bitmask X. We need to get sum of cnt[mask], when mask and X share at least one common bit having value 1 (formally (X AND mask) > 0). In order to do this, we need a reduction which may be not so obvious.
What if instead of counting all words containing at least one of vowels {w1, w2, ..., wk} we count all words which don't contain ANY of vowels {w1, w2, ..., wk}? Suppose this number is ret. Then, all words containing at least one of vowels is N — ret. From all words, we erase those words which do not contain any vowels from set {w1, w2, ..., wk} (and which obviously are wrong words). Obviously, it's left only words containing at least one vowel, so good words. Now, for a word not to contain any of vowels {w1, w2, ..., wk} it needs to contains ONLY vowels from set {"a", "b", "c", ..., "x"} \ {w1, w2, ..., wk} (set of allowed letters from which we erased vowels w1, w2, ..., wk}.
And this is reduction we needed. For a bitmask X we need to calculate sum of cnt[mask], where mask is a subset of X (we can set some bits from X from 1 to 0 in order to obtain mask). For a mask, let's keep this sum in res[mask]. We can calculate res array using divide and conquer.
Let's make a function solve(left, right), which completes array res in the way described above, if we consider only elements cnt[k] with left <= k < right (for simplicity, I'll consider elements which do not lie in this range to be equal to 0). Now we need to solve for a range [left, right]. Let's have in res1[] = solve(left, med) and in res2[] = solve(med, right), where med = (left + right) / 2. We need to put together res1[] and res2[] in order to obtain res[].
for (int i = left; i < med; ++i) res[i] = res1[i];
Numbers in [left, med] have most significant bit equal to 0. We can only keep it 0 and add what we calculated before. We can't add any element from res2[], because those elements have most significant bit equal to 1 and we're not allowed to change bit 0 into bit 1.
for (int i = med; i < right; ++i) res[i] = res1[i — med] + res2[i];
Here, most significant bit is 1. Adding res1[] corresponds to changing bit from 1 to 0, adding res2[] corresponds to leaving bit 1.
Of course, we need to threat the base case here, too. When left + 1 = right, res[left] = cnt[left]. We can keep only one array res[] instead of 3, I explained it this way only for simplicity. Also, there is no need for keeping separate arrays for res[] and cnt[], one can solve all task with only one array. In order to get res[], we simply call solve(0, 2^24).
Complexity of solution is O(2 ^ 24 * 24). I leave the proof homework, it's almost identical to complexity proof of D1 D "Author solution" (that with building a binary tree).
For a reference solution, check Endagorion's AC source during contest.











perfect editorial! thanks a lot!
Just would like to report a typo in 383D contestants' solution: the formula computes D[i+1][j] and not D[i][j]. Thanks for the quick editorial!
Thanks. Fixed.
sir i had a doubt i do understand how to calculate the atleast part in E, that just substract n — none case , but can i first caluclate the subsets value and than superset, that should give the answer
Like this first
c++ void forward2(vt<int>&dp){ rep(i , 0 , 24){ rep(j , 0 , dp.size()){ if(j & (1<<i)){ dp[j^(1<<i)] += dp[j]; } } } }than thisc++ void forward(vt<int>&dp){ rep(i , 0 , 24){ rep(j , 0 , dp.size()){ if(j & (1<<i) ){ dp[j] += dp[j ^ (1<<i)]; } } } }elfus has some of the best rounds on Codeforces, and definitely the best editorials. Congratulations to you and Rares for the round !
best editorial I have ever seen in codeforces
For Div 2C, if A[i] = A[j] = 0 and we put i before j, won't j lose milk? Or am I misinterpreting the solution?
One of the best editorials i came across in codeforces :D otherwise the editorial here are really very short and objective.
Every one here should write editorials like you :) !!
Finally a tutorial worth upvoting!
I didn't really need to think about D. As soon as I saw the constraint on , I decided to try a DP on (position,sum) — it was a massive hint for me. Well, sometimes it just happens that there's a simple solution, which the author doesn't realize :D. Maybe this could be eliminated by some extensive "problem testing" by random capable people?
, I decided to try a DP on (position,sum) — it was a massive hint for me. Well, sometimes it just happens that there's a simple solution, which the author doesn't realize :D. Maybe this could be eliminated by some extensive "problem testing" by random capable people?
I guess I was also lucky in not trying to solve B. I solved in the order: A (because it's easy), C (because I like it), D (because it's easy) :D
I've found a very short solution for Div2 C , by zxz5759209
I also had this solution and i got accepted but it took 1 hour to find it during the contest
Thanks for an informative editorial.
Unbelivable solution for Div2,B by Sick_Coder
A very good editorial, indeed! (but please don't forget about Div1E) And the problems were really nice. But I think problem B was tougher than it should have been for its amount of points. I've read some comments saying that problem B had too weak pretests (because so many solutions failed the final system tests). I would have to say that my experience with problem B was the exact opposite. I coded two wrong solutions (which failed some pretest or another) before eventually finding and implementing the right solution. So I'd say that problem B had good pretests :)
now this is a real editorial!! thanks guys :D
Hi,
Great and fast editorial with complete details.
Thanks very much.
Edit: I think there is a small typo: "It’s not hard to see that answer for a fixed (i1, j1) is left[i1][j1] * value[2 * j1 – sum_of_elements_from_i1]." I guess you meant count[2 * j1 – sum_of_elements_from_i1].
Best Editorials I have seen on codeforces yet! :D
For Propagating tree, how do we keep track of alternating levels in the arrays we created using DFS ?
Best Editorials Ever ! #thanks to the authors, for posting alternative solutions of contestants also. Great start in 2014. #Looking Forward.
Div1 E can be solved in O(2^24*24) or O(2^24+2^12*n)..
O(2^24*24): dp[i][s] means the sum of all contributions of subset s where all digits are same as s except the last i digits..
O(2^24+2^12*n): the length of word is only 3. We divide the 24 letters in half, calculate the answer for all first 12 letters and all last 12 letters and merge them with brute-force. This can be solved in O(2^24). Then we subtract the words that are counted twice: these words are words that have 2 letters in first half and 1 in second half, or 2 in second half and 1 in first half. Let's consider the first case: for each subset of first 12 letters we check each word whether it has exactly 2 letters in this half, if so, we can say all masks in another half that contains the third letter need to be subtracted by 1. This can be solved in 2^12*(2^12+n). Same algorithm can be used to solve the second case. Although this algorithm runs slower than O(2^24*24) bcuz of its larger constant...
Very nice editorial! Disappointed in Div 2B though, really expected the "real" problem rather than just insertion sort but that's what you get for not reading carefully ;)
However, does anyone have an accepted solution that is "real" (e.g. finds the minimum number of operations necessary and prints such a solution)? I was close but my computer died during contest and I haven't tried so much since (of course you can do O((mn)^2) easily but this is way too slow, there should be a O(n*m^2) solution but again my computer was unable to operate). My approach was to make 2-D boolean array to check if a swap is necessary, but I'm not sure if order of operations will end up being a big problem.
One of the best codeforces editorials ever! Thanks!
Thanks a lot. very good contest and good editorial too!
this is one of the best editorials on CF ever!!!
The best editorial I've read in a while here, thanks.
Hi, The way I print answers for 'Coder Problem' is as follows. This takes 124 ms. is there a way to print the answers faster ?
As the line contains k characters , and every odd lines are identical , also the even ones,
you can build 2 strings [C.C.C.C] and [.C.C.C.] and print them alternately
[In my opinion Java is slow language any way ]
Modulo operations are time consuming.
To check if a number
nis odd, you could useif (n & 1)i think there is a small bug in the pastie link u posted for the solution of Div1 C problem.
i submitted almost exact copy of it (5769615), but got WA#6. then i found the bug, corrected it and resubmitted (5769890) and got AC.
referring to my two submissions, corrections in line 68 (last statement of dfs) and line 109 (the second call to update).
Can you explain what exactly have you done in your submission (5769890) for this problem?
sorry bro i've forgotten ... that was over 6yrs ago now!
Hi, I tried to implement the Volcano problem in the way explained in the editorial but I'm getting TLE. Here is my code submission What am I doing wrong ? Thanks anyway.
Turns out my binary search is causing the problem and I don't see what is wrong with it... I would appreciate any ideas.
Wow! This really helped me a lot! Very detailed explanations!
It was by far your best round on Codeforces, fchirica. The problems were great, very different one from the other and some of them didn't require any algorithmic skills at all. Good job!
for div1 383C should end[5] = 7? edit: nvm drew the tree wrong
Great Editorial! Thanks so much, i've learned a lot!
Amazing solution by Endagorion.
In Div 1C problem, I could not understand how it can be solved using single fenwick tree from the solution link in the editorial. Can anyone please help.
Thanks
In Div.1 A I didn't catch the point that in 1st, quote : "If we put i before j, no additional cost will be added. Since j is in right of i and i only adds cost when it finds elements in left of i, j won’t be affected when processing i." Won't we lose milk if we put firstly i, in case of that j sees that and loses milk? Or am I misunderstanding the task?
I wonder how the problem Div1C can be converted to a segment tree lazy propagation implementation question, for trees like (1-2 2-3 3-4 4-5 .... 9999-E4) how can we achieve O(log N) update time?
а зачем в таске б массив он влияет как-то?
I'm getting Runtime Error on test 44 in Propogating Tree.
This is because of stack overflow right? That test has N = 2e5 and for a straight chain of nodes, I'll get a runtime error with a recursive DFS right? What to do in such cases?
I can write an iterative DFS, but I do HLD recursively too and I'm not quite sure if I can write an iterative HLD.
Can anyone tell me what to do in such cases? I'm assuming that I got the runtime error due to stackoverflow from DFS.
I used recursive dfs and passed all test case. Test 44 cost 1.5 s
How to solve DIV 1 C using one fenwick or segment tree. The code link given in editorial is not working.
[384E — Propagating tree] Can also be solved using Square Root Decomposition. Submission
I am Getting MLE on TC-53
Can someone review my code and figure out the issue ,Thanks