Sup, guys!
Let's consider the following problem: we have a set of strings (initially empty) and must handle two types of queries:
- Add new string to the set.
- For some input string do a check, if some string from the set occurs in the input string as a substring.
That's all. Of course, time/memory consuming should be as low as possible. Now I don't have an idea better than "Okay, let's use Aho-Corasick algo and each time, when we face query 1, let's destroy our old automaton and create a new one from scratch".
Thanks for your help.










A straightforward extension of your algorithm would be to partition the pattern set into groups of size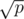 , where p is the number of patterns. Then you only need to rebuild the automaton for
, where p is the number of patterns. Then you only need to rebuild the automaton for 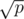 pattern strings. Queries will also be slower by a factor of
pattern strings. Queries will also be slower by a factor of 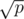 .
.
Thanks, that's a good idea, but let me ask a question: why sqrt? I know about general sqrt-decomposition approach, but I've always been interested, why exactly P^(1/2), not P^(1/3) or log(P) or something like that? Is there some kind of proof that "sqrt is better"?
The thing is, you can chose any factor k. Then your query time is multiplied by k and your update time is divided by k. So your query time becomes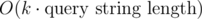 and your update time becomes
and your update time becomes 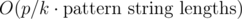 . We want to optimize the worst case, so we chose k such that max(k, p / k) is minimal. It just so happens that
. We want to optimize the worst case, so we chose k such that max(k, p / k) is minimal. It just so happens that 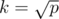 is the optimal choice because then k = p / k in that case.
is the optimal choice because then k = p / k in that case.
I ignored some factors here that are dependent on the string lengths, so if there are certain restrictions on how long your query strings and patterns strings can get, than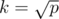 might not be the optimal choice. You could for example group the pattern strings by length.
might not be the optimal choice. You could for example group the pattern strings by length.
Forget the algorithm below, since it's not working.
Here's a variant that uses hashing to achieve poly-logaritmic time:
O(log n)wherenis the minimum of the lengths of those substrings.s, for every suffixs[i..|s|], locate its neighbors in the BBST and check whether one of them is a prefix of the suffix.The total runtime is quadratically logarithmic in the input size. It would be interesting to see a variant of this that doesn't rely on hashing. It would also be interesting to see whether we can shave of one of the log factors.
Is this a real problem somewhere? I'd like to try an implementation of this.
The nearest neighbor could be some string in between, no? Like, if you have strings {abc,abca,abcd}, then the nearest neighbors of abcc could be abca and abcd, no?
You're correct. Let me try to revise the algorithm to fix that (although I'm not sure it's possible with this approach).
Nope, it's not a problem from online-judge/contest/etc, just a kind of work I've faced during my university "research".
If you are not looking for the "online" solution, just look at the problem 163E - e-Government and its editorial.
What about this solution:
Let's say that we're looking for all strings s from the set S that are prefixes of string T (T is a suffix of our input string, and we can do this for all suffixes independently). If a string si matches, and a string sj longer than sj matches, then si must be a prefix of sj. So if we could bin-search the longest prefix that's "good" somehow, like the longest prefix that's common with some string from S, we could just get the complete information from it...
The most obvious first choice is storing the hashes of all string in S and bin-searching the longest prefix of T which has the same hash as one of the stored ones. Well, for that to work, we need all prefixes of all strings in S, and after thinking a bit, we can find out that it's better to store the strings of S in a trie, store hashes of all vertices and bin-search the deepest vertex. Since we're just adding strings and extending the trie, we can update the map of (hash,vertex) easily when adding a string to S.
This "prefix to trie vertex" method is cool, because it allows us to replace a substring by an interval (corresponding to a subtree of the trie). Still, it's not of much use if the question's about the number of occurences or number of strings from S that occur in the input string — the trie's dynamic, so standard approaches (standard interval tree, LCA preprocessing or HLD) fail on it. I still wonder if there's a solution to that. Luckily, the question here is just about some occurence.
Let's add one more information to the trie: each vertex will have a dead/alive status. A dead vertex corresponds to a prefix that has a string from S as a (possibly equal) substring. This status is inherited — if we add a vertex, it'd have the same status as its son. Also, after adding a string to the trie, we must mark its end vertex as dead, and mark all its successors as dead as well — we can just traverse the subtree by DFS, plus utilize the property that if a vertex was dead before, then its whole subtree was dead before, so we don't need to go deeper. In order to do that efficiently, we'd also keep a list of just living sons for every vertex; when marking the top node of a subtree as dead, we can just remove the link from its parent, and we can DFS by those special links. Note that we also need a separate list of all sons, for standard "add a string to the trie" operation.
With this, we can easily check if some string from S occurs in T as a substring — iff the vertex we found was dead, the answer's yes. The answer for the whole string is yes iff the answer for some suffix T is yes.
We only mark a node as dead at most once, and we mark every node traversed in the DFS as dead, so if the total length of strings from operations 1 is L1, the total and maximum lengths from op. 2 are L2 and l, then the time complexity is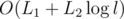 .
.
I wonder if this actually works — it just looks really simple compared to suffix whatever structures and Aho-Corasick.
"bin-searching the longest prefix of T which has the same hash as one of the stored ones."
Wouldn't we have a very similar problem here as with the BBST nearest neighbor? Say we have patterns "abc" and "abcde" and query string suffix "abcdf". Binary search would tell us that "abcd" is the longest prefix of the query string that is also a prefix of one of the patterns, but we can't find "abc" from that. Did I misunderstand something here?
Oh I see, nevermind. When using a trie it's pretty obvious how to resolve this.
There is a solution using AC Automaton.
When we have N strings in the set, maintain logN AC Automatons : the ith automaton contains the first 2ki strings not included in previous automatons, where ki is position of the ith highest 1 in binary representation of N. For example when N = 19, we have 3 automatons : {S1..S16}, {S17..S18} and {S19}.
The first type of operation can solved by traversing the logN automatons using the given string.
When adding a string, first construct a automaton using the single string, and while there are two automatons with the same number of strings, we merge them by construct a new automaton using brute force. It's easy to see the property in the first paragraph keeps, and the complexity of the algorithm is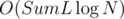 , where SumL is the total length of all strings, and N is the number of insert operations.
, where SumL is the total length of all strings, and N is the number of insert operations.
Thanks a lot, it is really elegant solution. Actually, it has been already described in this thread in Russian. Thank you anyway! Let me ask a question: have you invented this idea by yourself or read/heard about it somewhere?
What about my solution with trie, hashes, bin-search and DFS? :D
sillycross wrote about this technique one year ago. Now it's widely known among Chinese coders.