In August 2022, I had a talk concerning lattice paths at a summer programming school in Khust, Ukraine. After, I realised that some aspects of my talk aren't well-known in the CP community and, in this blogpost, I'd like to very briefly and untidily (so feel free to ask for additional explanations by comments) share the main points of that talk.
I hope that ideas presented in the blog will help you sometime.
1. Lattice paths
1.1. Walks without restrictions.
1.1.1. We start from a rudimentary example. Consider a $$$N\times M$$$ grid and a robot (or a chip, or a ship, or anything else you wish) at $$$(0,0)$$$ (not a cell, an intersection point) which can move in the east unit direction and in the north unit direction. A route that the robot is able to make is said to be northeastern. How many northeastern paths are there? In fact, We can bijectively code any path with a corresponding string of the form $$$\uparrow\rightarrow\rightarrow\rightarrow\uparrow\rightarrow\dots$$$ of length $$$N+M$$$. There are $$$N$$$ places to put $$$\rightarrow$$$ hence there are $$$\binom{N+M}{N}$$$ such paths.
1.1.2. One can easily generalise this formula to a $$$d$$$-dimensional case. Indeed, consider a $$$d$$$-dimensional box (grid) $$$[N_1]\times [N_2]\times \dots\times [N_d]$$$ (where $$$[M] = {1,\dots,M}$$$). Then, the robot can make steps which are from the orthonormal basis i. e. $$$\mathbf{e}_1=(1,0,\dots,0)$$$, $$$\mathbf{e}_2=(0,1,\dots,0)$$$, $$$\dots$$$, $$$\mathbf{e}_d = (0,0,\dots,1)$$$. Then, the string consists of the numbers between $$$1$$$ and $$$d$$$ which represent the steps of the robot. We have $$$N_1+\dots+N_d$$$ steps in total: $$$N_1$$$ steps correspond to $$$\mathbf{e}_1$$$, $$$N_2$$$ steps correspond to $$$\mathbf{e}_2$$$, etc. There are $$$N_1+N_2+\dots+N_d$$$ "free" seats for the steps of the first kind, $$$N_2+\dots+N_d$$$ `free' seats for the steps of the second kind and etc. Hence, there are
paths. One may do some algebra and obtain a splendid formula which, in fact, is a multinomial coefficient that appears in a generalisation of the binomial theorem
1.1.2*. It is worth saying several words about a geometric interpretation of the multinomial theorem. For the sake of exposition, the only case we explain is $$$d=2$$$, just because we can simply draw and imagine it. Consider an infinite grid with origin $$$(0,0)$$$ and with blue horizontal and red vertical lines. Let the cost of the blue unit segment be $$$a$$$ and the cost of the red unit segment be $$$b$$$ (as monomials, not numbers). The cost of a path is a product of all the unit segments in it. That is the cost of a path which consists of 4 horizontal and 3 vertical unit steps is $$$a^4b^3$$$. So,
The $$$d$$$-dimensional formula is
1.2. Catalan numbers
1.2.1 Almost everyone knows about Catalan numbers, yet, as a prelude we demonstrate the first implementation of the reflection method (André reflection method), we shall write a bit about the combinatorial derivation of the closed form. Indeed, the first natural question, after 1.1 is about the number of paths under some restrictions. How many northeastern paths from $$$(a,b)$$$ to $$$(c,d)$$$ which lie under $$$y=x$$$ are there (we additionally assume $$$a\geq b$$$ and $$$c\geq d$$$ to avoid pitfalls).
1.2.2. The first caveat is that it is allowed to touch $$$y=x$$$, which, in fact, is an intersection. Instead, we consider a shifted line $$$y=x+1$$$. Then, any intersection (including touching) with $$$y=x+1$$$ is forbidden and now we can safely touch the line $$$y=x$$$. We also shall count the number of bad paths (which intersects $$$y=x+1$$$) and then we shall just subtract this number from the total one: $$$\binom{c-a+d-b}{c-a}$$$ (according to 1.1).
1.2.3. Consider any bad path from $$$(a,b)$$$ to $$$(c,d)$$$ (such path exists because of $$$a\geq b$$$ and $$$c\geq d$$$) and the first intersection point with $$$y=x+1$$$. Reflect this path with respect to this line and we thus obtain a bad path from $$$(a,b)$$$ to $$$(d-1,c+1)$$$. Moreover, any path from $$$(a,b)$$$ to $$$(d-1,c+1)$$$ definitely intersects $$$y=x+1$$$ and therefore is bad. So, we obtained the bijection between bad paths and all paths between $$$(a,b)$$$ and $$$(d-1,c+1)$$$. There are exactly, again by 1.1, $$$\binom{c-a+d-b}{c-b+1}$$$ such paths.
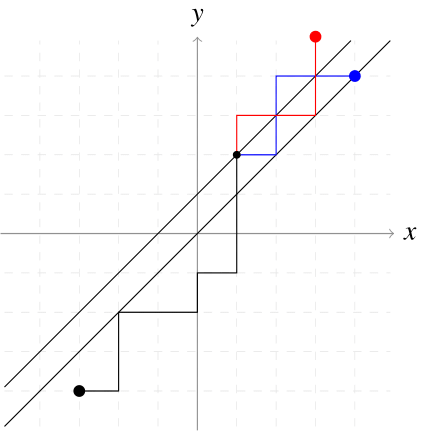
Therefore, the number of under-$$$y=x$$$ paths is equal to
In particular, when $$$a=b=0$$$ and $$$c=d=N$$$ we obtain
2. The reflection method on graphs
This section will be about Lindstrom-Gessel-Viennot lemma, yet for the sake of exposition, we present a non-weighted version.
2.1.1. Definitions
2.1.1. Let $$$G$$$ be an oriented acyclic graph. Consider two sets of vertices
Note that $$$n$$$ is the same for both sets.
2.1.2. Introduce a path matrix $$$M_G(\mathbf{A},\mathbf{B})$$$ (when one can easily recover $$$G$$$, $$$\textbf{A}$$$ and $$$\mathbf{B}$$$ from the context, we shall abridge the notation and simply write $$$M$$$). Let $$$M_{ij}$$$ be equal to the number of paths from $$$A_i$$$ to $$$B_j$$$. Note that this number is well-defined since $$$G$$$ is acyclic.
2.1.3. A path system $$$\mathbf{P}_\pi (\mathbf{A}, \mathbf{B})$$$ (where $$$\pi$$$ is a permutation of $$${1,\dots,n}$$$) is a set of paths
Note that the existence of multiple paths between two vertices is possible, and consequently, it's not guaranteed that a path system is unique. A path system is said to be disjoint if there is no vertex which belongs to two or more paths.
2.2. Unweighted LGV-lemma
2.2.1. We are ready to state the unweighted LGV-lemma.
Lemma. For any acyclic oriented graph $$$G$$$ and two sets (of the same size) $$$\mathbf{A}, \mathbf{B}$$$ of its vertices it holds that
2.2.2. We write the definition of determinant.
Recall that $$$M_{1\pi_1}$$$ is the number of paths from $$$A_1$$$ to $$$B_{\pi_1}$$$, ..., $$$M_{n\pi_n}$$$ is the number of paths from $$$A_n$$$ to $$$B_{\pi_n}$$$. Their product $$$M_{1\pi_1} M_{2\pi_2} \dots M_{n\pi_n}$$$ is the total number of paths systems with the fixed permutation $$$\pi$$$. See the picture below.
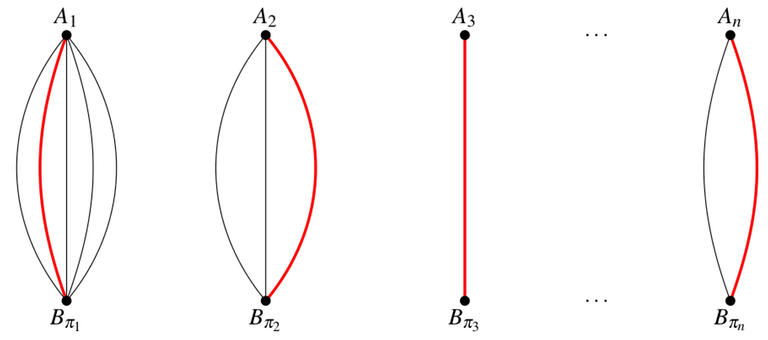
Therefore, we obtain the following formula
2.2.3. In 2.2.2 we proved that sum of signs over all path systems is equal to the determinant. So, the rest is to prove
2.2.4. Let $$$\mathbf{P}_\pi$$$ be an intersecting path system. Consider the smallest `bad' $$$i$$$ such that $$$A_i \to B_{\pi_i}$$$ shares some vertex. Let $$$X$$$ be the first such vertex and $$$j$$$ be the smallest $$$j>i$$$ such that path $$$A_j \to B_{\pi_j}$$$ contains $$$X$$$. We construct a new path system by swapping:
And the picture:
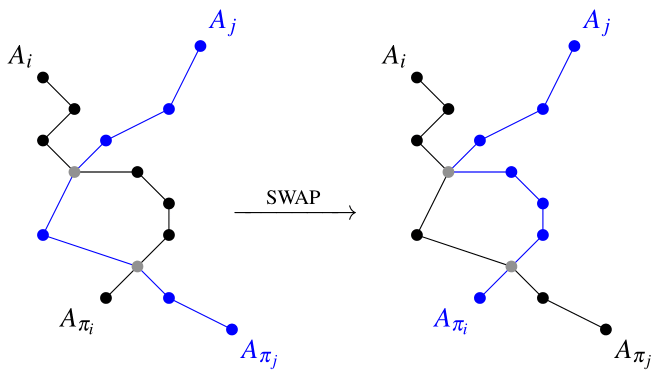
2.2.5. The rest is the analysis of this highly elegant construction. However, we prefer to incautiously say that it's an involution and hence a bijection on the set of intersecting path systems, yet one may check it explicitly and carefully. Moreover, SWAP makes a transposition and hence changes the parity of the permutation $$$\pi$$$. So,
And hence the claim asked in 2.2.3 holds. Congratulations, your repertoire was enhanced with LGV-lemma!
3. Applications
3.1. The very first application
The graph, in this section, is just a large portion of the northeastern infinite grid graph.
3.1.1. Let $$$a_1<\dots<a_N$$$ and $$$b_1<\dots<b_N$$$ be sequences of nonnegative integers. Then the number of paths systems from $$$\mathbf{A} = {(0,a_i)}$$$ to $$$\mathbf{B} = {(K,b_i)}$$$ (where $$$K$$$ is some fixed number) can be computed as determinant
Indeed, since $$$a_1<\dots<a_N$$$ and $$$b_1<\dots<b_N$$$ the only one disjoint paths system is identity system: $$$A_i \to B_i$$$ for all possible $$$i$$$. The rest is the application of LGV-lemma. An example problem: 348D - Turtles.
3.1.2. Another variation of the first example is the following: how many paths $$$(0,0)$$$ to $$$(N,M)$$$ are there if it's forbidden to touch any of given $$$K$$$ points, say $$$(x_1,y_1)$$$, ..., $$$(x_K, y_K)$$$?
Introduce two sets $$$\mathbf{A} = ((0,0); (x_1,y_1); \dots; (x_K,y_K))$$$ and $$$\mathbf{B} = ((N,M); (x_1,y_1); \dots; (x_K,y_K))$$$. It's easy to realise that any disjoint paths system is identity one. Since it's disjoint we can intersect (and particularly even touch) paths $$$(x_i,y_i)\to (x_i,y_i)$$$, which, in fact, are our forbidden points. So, the answer to the problem is $$$\det M(\mathbf{A},\mathbf{B})$$$.
3.2. Plane partitions
3.2.1. How many plane partitions in a box $$$a\times b\times c$$$ are there?
3.2.2. Recall, that plane partition is just a chain of included Young diagrams. Yet, a Young diagram is just a lattice path. So, a plane partition is just a collection of `almost disjoint paths. We shift these paths in order to obtain a disjoint paths system.
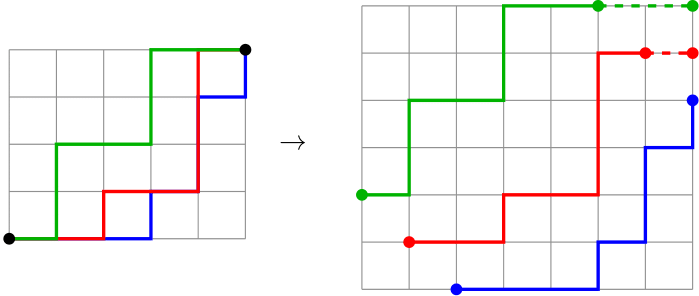
So,
The rest is the algebra:
Use Pochhammer symbols:
This one is, in fact, Vandermonde determinant, which can be evaluated explicitly:
We can continue
Return back,
So, the final $$$O(a+b+c)$$$ formula is
3.3. Miscellaneous
This `reflection method' can be used to prove hook-length formula.
You can also can enjoy with one more problem from AtCoder.











I think that this blog is a little advanced for me , but I saved it for later! Thank you!
I read section 1 and 2. They are very clear. It was a quick read and I learnt something, thank you very much.
In the next days I will take a look at the problems listed in section 3, trying to solve them on my own.
I have a question about the intersecting systems, particularly about point 2.2.5. Consider the following example:
$$$A = (1, 2, 3), B = (11, 12, 13)$$$ and an intersecting path system $$$P_\pi = ((1, 5, 8, 11), (2, 6, 9, 12), (3, 4, 5, 7, 9, 10, 13))$$$ (assuming that all the required edges exist). Let's try to construct the corresponding path system. We see, that paths $$$A_1 \to B_1$$$ and $$$A_2 \to B_2$$$ do not intersect, thus the lexicographically minimal intersecting pair is $$$(1, 3)$$$. Thus, the new path system is $$$P_{\pi'} = ((1, 5, 7, 9, 10, 13), (2, 6, 9, 12), (3, 4, 5, 8, 11))$$$.
Now, let's try to construct the new path system one more time. Now $$$A_1 \to B_{\pi' 1}$$$ and $$$A_2 \to B_{\pi' 2}$$$ do intersect, so the matching pair is $$$(1, 2)$$$ and we obtain $$$P_{\pi"} = ((1, 5, 7, 9, 12), (2, 6, 9, 10, 13), (3, 4, 5, 8, 11))$$$ which is not the same as $$$P_\pi$$$.
I understand that this is some technicality but I don't seem to understand how the construction leads to an involution.
I'm tempted to believe that if the order of selection in the algorithm was reversed, we would have an involution. What I mean by that is that first we select the minimal vertex that is included in several paths and among those paths we select the lexicographically minimal pair of indices.
In such case, in the above example we would be forced to not select pair $$$(1, 2)$$$ in the second construction, as vertex $$$5$$$ (belonging to the desired pair $$$(1, 3)$$$) has lower value than $$$9$$$.
You are quite right. I've just fixed it, thank you! It seems that your way (find a vertex with the smallest index and the first pair) is also acceptable, yet in that case, we need to enumerate the vertices.
Very nice blog!
Out of curiosity, do you know of some application of the LGV lemma that doesn't involve the "trick" where we force the only valid permutation to be the identity one? (perhaps apart from ones where the answer is to be computed modulo 2 or something like that)
Thank you, that's an interesting question!
Outside of the competitive programming context, there are, for instance, proofs of the Cauchy-Binet formula and matrix-tree theorem…
I think that the power of the lemma comes from its shape: det = a sum over something specific, and if we are able to give a meaningful interpretation of the sum (in particular, it's easy when the only system is the identity, the "trick") then we can compute it with a determinant. However, This reasoning is just a plausible explanation of why the "trick" is crucial here. I probably don't know any enumerative results without it.
On the other hand, as in the example of the Cauchy-Binet formula, we can establish results on determinants by manipulating the sums over objects with enhanced combinatorial structure, which may be easier than usual. I think it's the main field of "trick"-free applications.