We hope you liked the problems! Unfortunately, problem C turned out to be harder than usual. Please read its editorial, we hope you'll find that the intended solution is not that hard.
1763A - Absolute Maximization
Idea: DreadArceus
Prepared by: DreadArceus
Which $$$1$$$s in the binary representation cannot be changed to $$$0$$$.
Similarly, Which $$$0$$$s in the binary representation cannot be changed to $$$1$$$.
Considering the last two hints, try to maximize the maximum element and minimize the minimum element.
In the minimum element, we want to make every bit $$$0$$$ when possible, it won't be possible to set a particular bit to $$$0$$$ when that bit is set in all the elements of $$$a$$$. Therefore, the minimum value we can achieve after performing the operations is the bitwise AND of all the elements of $$$a$$$.
In the maximum element, we want to make every bit $$$1$$$ when possible, it won’t be possible to set a particular bit to $$$1$$$ when that bit is not set in any of the elements of $$$a$$$. Therefore, the maximum value we can achieve after performing the operations is the bitwise OR of all the elements of $$$a$$$.
Therefore the answer is (OR of the array — AND of the array).
Time Complexity: $$$O(n)$$$
1763B - Incinerate
What if the array $$$p$$$ was sorted?
Is it necessary to decrease the health of each monster manually after every attack?
Sort the monsters in ascending order of their powers.
Now we iterate through the monsters while maintaining the current attack power and the total damage dealt.
Only the monsters with health greater than the total damage dealt are considered alive, and every time we encounter such a monster it will be the weakest one at the current time, thus we need to attack until the total damage dealt exceeds the current monster's health while lowering our attack power by its power each time.
If we can kill all the monsters in this way, the answer is YES, otherwise it is NO.
Time Complexity: $$$O(nlogn)$$$
Code Author: DreadArceus
Sort the monsters in ascending order of their health.
Now we maintain a count of monsters alive after each attack. This could be achieved by applying $$$upper bound()$$$ on $$$h$$$ array for each attack. The total damage dealt could be stored and updated in a separate variable.
To find the power of the weakest monster alive, we could just precompute the minimum power of monsters in a suffix array. In other words,
Time Complexity: $$$O(nlogn)$$$
1763C - Another Array Problem
Idea: .utk.
Prepared by: .utk.
What happens when we apply the same operation twice?
What about n = 3 ?
Let’s first consider the case for $$$n \geq 4$$$. The key observation to make here is that we can make all the elements of a subarray $$$a_l,...a_r$$$ zero by applying the operation on range $$$[l,r]$$$ twice. Then let’s assume the maximum element $$$mx$$$ of the array is at an index $$$m > r$$$. We can apply the operation on the range $$$[l,m]$$$ and turn all its elements into $$$mx$$$.
Using the above information we can see that to achieve the final array with maximum sum we need to make all the elements in it equal to the maximum element in the array. Regardless of the given array this can be achieved by making the last two elements (n-1,n) zero. Then applying the operation on subarray $$$[m,n]$$$ to make all its elements equal to $$$mx$$$. Then making the first two elements (1,2) zero and applying the operation on the whole array making all the elements equal to $$$mx$$$. Thus the maximum sum for the final array will always be $$$n*mx$$$. (In case $$$m = n-1$$$ or $$$n$$$, we can operate on the left side first to reach the same solution).
For $$$n = 2$$$ the maximum final sum would be $$$\max(a_1+a_2, 2*(|a_1-a_2|))$$$.
For $$$n=3$$$, when the maximum element is present at index $$$1$$$ or $$$3$$$ we can make all the elements of the array into $$$mx$$$. When the maximum element is at index $$$2$$$, we have the following options.
Case 1: We can apply the operation on (1,2), then we can convert all the elements of the array into $$$ \max(a_3,|a_2-a_1|)$$$.
Case 2: We can apply the operation on (2,3), then we can convert all the elements of the array into $$$ \max(a_1,|a_2-a_3|)$$$.
Case 3: We can apply the operation on (1,3) making all the elements in the array $$$|a_1-a_3|$$$. This is redundant since $$$a_2 > a_1,a_3$$$ either case 1 or case 2 will give a larger sum as $$$a_2 - \min(a_1,a_3) > \max(a_1,a_3) - \min(a_1,a_3)$$$.
Now considering case 1, if $$$ 3* \max(a_3,|a_2-a_1|) \leq a_1+a_2+a_3 $$$ the maximum sum possible would be the current sum of the array (see sample 1 and 3). Therefore no operations are required. Similar case for case 2.
So the maximum possible sum for $$$n=3$$$ will be $$$\max(3*a_1, 3*a_3, 3*|a_1-a_2|, 3*|a_3-a_2|,a_1+a_2+a_3)$$$.
To avoid doing this casework for $$$n = 3$$$, we can see that there are only 3 possible operations -> (1,2) , (2,3), (1,3). We will be required to perform operations (1,2) and (2,3) at most two times. So we can brute force all possible combinations of operations [(1,2),(1,2),(2,3),(2,3),(1,3)] to find the maximum sum.
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define pii pair<ll, ll>
int32_t mod = 1e9 + 7;
void solve()
{
ll n;
cin >> n;
vector<ll> a(n);
for (auto &i : a)
cin >> i;
if (n == 2)
cout << max({2 * abs(a[0] - a[1]), a[0] + a[1]});
else if (n == 3)
cout << max({3 * (abs(a[0] - a[1])), 3 * (abs(a[2] - a[1])), 3 * a[0], 3 * a[2], a[0] + a[1] + a[2]});
else
{
ll mx = 0;
for (auto i : a)
mx = max(i, mx);
cout << n * mx;
}
cout<<'\n';
}
int32_t main()
{
ios::sync_with_stdio(false), cin.tie(NULL);
ll t = 0;
cin >> t;
while (t--)
solve();
}
Author: .utk.
1763D - Valid Bitonic Permutations
Idea: warks
Prepared by: warks
Can you solve the problem when $$$x < y$$$?
When $$$x > y$$$, perform $$$i'=n-j+1$$$, $$$j'=n-i +1$$$, $$$x' = y$$$, and $$$y' = x$$$.
Can you solve the problem for a fixed value of $$$k$$$?
Iterate over possible values of $$$k$$$. The total count is the sum of the individual counts.
Club the remaining numbers into ranges as follows: $$$[1,x-1]$$$, $$$[x+1,y-1]$$$, and $$$[y+1,n-1]$$$.
For simplicity, if $$$x > y$$$, perform $$$i' = n-j+1$$$, $$$j' = n-i+1$$$, $$$x' = y$$$, and $$$y' = x$$$. Hereafter, the variables $$$i$$$, $$$j$$$, $$$x$$$, and $$$y$$$, will refer to these values. Now, $$$i < j$$$ and $$$x < y$$$.
For now, assume that $$$y < n$$$. We shall consider the case where $$$y = n$$$ at a later stage.
Let us consider solving the problem for fixed $$$k$$$. Valid values for $$$k$$$ are $$$[2,i-1]$$$, $$$[i+1,j-1]$$$, $$$[j+1,n-1]$$$.
If we think about it, when $$$x < y$$$, $$$k$$$ cannot lie in the range $$$[2, i-1]$$$. So, we can discard them as possible values for $$$k$$$.
Let us consider the case where $$$k$$$ belongs to $$$[i+1,j-1]$$$.
The permutation adheres to the following pattern: $$$B_1 < .. < B_i = x < .. < B_k = n > .. > B_j = y > .. > B_n$$$.
- Numbers to the left of $$$i$$$ must lie in the range $$$[1,x-1]$$$. We choose $$$i-1$$$ elements from $$$[1,x-1]$$$ and place them to the left of $$$i$$$. There are $$${x-1 \choose i-1}$$$ ways to do this. The remaining $$$x-i$$$ elements from $$$[1,x-1]$$$ lie to the right of $$$j$$$ by default.
- Numbers to the right of $$$j$$$ must lie in the range $$$[1,x-1]$$$ or $$$[x+1,y-1]$$$. Since numbers in the range $$$[1,x-1]$$$ have already been placed, therefore, we choose numbers in the range $$$[x+1,y-1]$$$, and place them in the $$$n-j-(x-i)$$$ remaining positions. There are $$${y-x-1 \choose n-j-(x-i)}$$$ ways to do this. The remaining elements in the range $$$[x+1,y-1]$$$ lie between $$$i$$$ and $$$k$$$ by default.
- Numbers between $$$k$$$ and $$$j$$$ must lie in the range $$$[y+1,n-1]$$$. We choose $$$j-k-1$$$ elements from $$$[y+1,n-1]$$$ and place them between $$$k$$$ and $$$j$$$. There are $$${n-y-1 \choose j-k-1}$$$ ways to do this. Afterwards, the remaining elements in the range lie between $$$i$$$ and $$$k$$$ by default, and the permutation is full.
Let us consider the case where $$$k$$$ belongs to the range $$$[j+1,n-1]$$$.
The permutation adheres to the following pattern: $$$B_1 < .. < B_i = x < .. < B_j= y < .. < B_k = n > .. > B_n$$$.
- Similar to above, the numbers to the left of $$$i$$$ must lie in the range $$$[1,x-1]$$$. We choose $$$i-1$$$ elements from $$$[1,x-1]$$$, and place them to the left of $$$i$$$. The remaining $$$x-i$$$ elements from $$$[1,x-1]$$$ lie to the right of $$$k$$$ by default.
- Numbers between $$$i$$$ and $$$j$$$ must lie in the range $$$[x+1,y-1]$$$. We choose $$$j-i-1$$$ elements from $$$[x+1,y-1]$$$ and place them between $$$i$$$ and $$$j$$$. There are $$${y-x-1 \choose j-i-1}$$$ ways to do this, and the remaining elements from $$$[x+1,y-1]$$$ lie to the right of $$$k$$$ by default.
- Numbers between $$$j$$$ and $$$k$$$ must lie in the range $$$[y+1,n-1]$$$. We choose $$$k-j-1$$$ elements from $$$[y+1,n-1]$$$ and place them in these positions. Afterwards, the remaining elements in the range get placed to the right of $$$k$$$ by default, and the permutation is full.
The answer to the problem is the sum of individual answers for all iterated values of $$$k$$$.
Let us now consider the case where $$$y = n$$$.
The permutation adheres to the following pattern: $$$B_1 < .. < B_i = x < .. < B_j = B_k = n > .. > B_n$$$.
- Again, the numbers to the left of $$$i$$$ must lie in the range $$$[1,x-1]$$$. We choose $$$i-1$$$ elements from $$$[1,x-1]$$$ and place them to the left of $$$i$$$. The remaining $$$x-i$$$ elements from $$$[1,x-1]$$$ lie to the right of $$$j$$$ (here, $$$k$$$) by default.
- Numbers between $$$i$$$ and $$$j$$$ must lie in the range $$$[x+1,y-1]$$$. We choose $$$j-i-1$$$ elements form $$$[x+1,y-1]$$$ and place them between $$$i$$$ and $$$j$$$. The remaining elements from $$$[x+1,y-1]$$$ lie to the right of $$$j$$$ (here, $$$k$$$) by default, and the permutation is full.
With $$$O(n_{max}*log(10^9+7-2))$$$ precomputation for factorials and their modular inverses, each individual test can be solved as above in $$$O(n)$$$. Therefore, the overall complexity of this approach is $$$O(n_{max}*log(10^9+7-2) + t*n)$$$, but the constraints allowed for slower solutions as well.
$$$Bonus:$$$ Can you solve the problem when $$$1 \le t, n \le 10^5$$$.
#include <iostream>
#include <vector>
using namespace std;
const int MOD = 1000000007;
vector<int> fac;
vector<int> ifac;
int binExp(int base, int exp) {
base %= MOD;
int res = 1;
while (exp > 0) {
if (exp & 1) {
res = (int) ((long long) res * base % MOD);
}
base = (int) ((long long) base * base % MOD);
exp >>= 1;
}
return res;
}
void precompute(int n) {
fac.resize(n + 1);
fac[0] = fac[1] = 1;
for (int i = 2; i <= n; i++) {
fac[i] = (int) ((long long) i * fac[i-1] % MOD);
}
ifac.resize(n + 1);
for (int i = 0; i < fac.size(); i++) {
ifac[i] = binExp(fac[i], MOD - 2);
}
return;
}
int nCr(int n, int r) {
if ((n < 0) || (r < 0) || (r > n)) {
return 0;
}
return (int) ((long long) fac[n] * ifac[r] % MOD * ifac[n - r] % MOD);
}
int countValidBitonicPerm(int n, int i, int j, int x, int y) {
if (x > y) {
i = n - i + 1;
j = n - j + 1;
swap(i, j);
swap(x, y);
}
int sum = 0;
for (int k = i + 1; k < j; k++) {
sum += nCr(n - y - 1, j - k - 1);
sum %= MOD;
}
int count = (int) ((long long) nCr (x - 1, i - 1) * nCr(y - x - 1, n - j - (x - i)) % MOD * sum % MOD);
sum = 0;
for (int k = j + 1; k < n; k++) {
sum += nCr(n - y - 1, k - j - 1);
sum %= MOD;
}
count += (int) ((long long) nCr(x - 1, i - 1) * nCr(y - x - 1, j - i - 1) % MOD * sum % MOD);
count %= MOD;
if (y == n) {
if (j == n) {
return 0;
} else {
return (int) ((long long) nCr(x - 1, i - 1) * nCr(y - x - 1, j - i - 1) % MOD);
}
}
return count;
}
int main() {
const int MAXN = 100;
precompute(MAXN);
int testCases;
cin >> testCases;
for (int test = 1; test <= testCases; test++) {
int n, i, j, x, y;
cin >> n >> i >> j >> x >> y;
cout << countValidBitonicPerm(n, i, j, x, y) << endl;
}
return 0;
}
1763E - Node Pairs
Idea: crimsonred
Prepared by: ...nvm, DreadArceus, crimsonred
In a directed graph, which nodes are reachable from each other? How many such pairs of nodes exist?
Think about a sequence of SCCs.
For two nodes $$$u$$$ and $$$v$$$ to be reachable from each other, they must lie in the same strongly connected component (SCC). Let's define $$$f(i)$$$ as the minimum number of nodes required to construct an $$$i$$$-reachable graph. We can use dynamic programming and calculate $$$f(i)$$$ as $$$f(i) = \min(f(i — \frac{s (s — 1)}{2}) + s)$$$ over all the valid SCC sizes $$$s$$$ for which $$$\frac{s (s — 1)}{2} \leq i$$$, i.e., over those $$$s$$$ which have less pairs of the required type than $$$i$$$. Thus, $$$f(p)$$$ gives us the minimum number of nodes required to create a $$$p$$$-reachable graph.
In all $$$p$$$-reachable graphs with $$$f(p)$$$ nodes, the upper bound on the number of unidirectional pairs of nodes is $$$\binom{f(p)}{2} - p$$$, because we have exactly $$$p$$$ pairs of nodes which are reachable from each other. It is possible to achieve this upper bound using the following construction: let $$$s_1, s_2, \ldots, s_k$$$ be any sequence of SCC sizes which agrees with the dp values we calculated earlier. Let the first SCC contain the nodes $$$[1, s_1]$$$, the second one contain $$$[s_1 + 1, s_1 + s_2]$$$, and so on. We add a directed edge from $$$u$$$ to $$$v$$$ if $$$u < v$$$.
Time Complexity: $$$\mathcal{O}(p\sqrt{p})$$$
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9;
void solve()
{
int p;
cin >> p;
vector<int> dp(p + 1, INF);
dp[0] = 0;
for (int i = 1; i <= p; ++i)
for (int s = 1; (s * (s - 1)) / 2 <= i; ++s)
dp[i] = min(dp[i], dp[i - (s * (s - 1)) / 2] + s);
cout << dp[p] << ' ' << ((long long) dp[p] * (dp[p] - 1)) / 2 - p << '\n';
}
int main()
{
solve();
return 0;
}
1763F - Edge Queries
Idea: ...nvm, DreadArceus
Prepared by: ...nvm, DreadArceus
What kind of graph meets the conditions given in the statement?
A graph with bridges connecting components with a hamiltonian cycle.
Which edges will never be counted in answer to any query?
Of course, the bridges.
Restructure the graph to be able to answer queries.
$$$query(u, v)$$$ on a tree can be solved efficiently via Lowest Common Ancestor (LCA).
First, let us see examples of graphs that are valid or invalid according to the statement.

In this graph, for node $$$4$$$, the longest simple cycle is $$$4 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 4$$$.
$$$S_4 = {1, 2, 3, 4}$$$
All simple cycles from node $$$4$$$ are $$$4 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 4$$$ and $$$4 \rightarrow 1 \rightarrow 3 \rightarrow 4$$$.
$$$C_4 = {1, 2, 3, 4}$$$
So, $$$S_4 = C_4$$$. Similarly, $$$S_u = C_u$$$ for all $$$u$$$.
A tree of such components is also a valid graph!
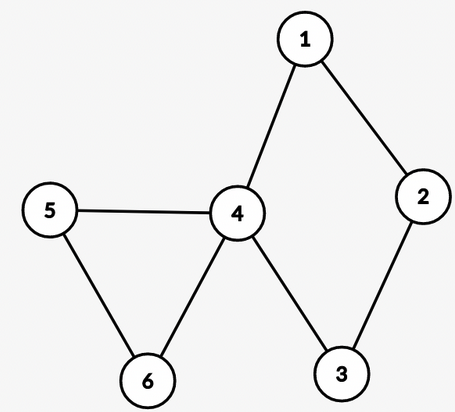
Here, $$$S_4 = {1, 2, 3, 4}$$$ and $$$C_4 = {1, 2, 3, 4, 5, 6}$$$.
So, $$$S_4 \neq C_4$$$
The queries ask us to count all non-bridge edges in any simple path from $$$u$$$ to $$$v$$$.
There are many ways to proceed with the solution. We will first go into a simple one that gives more insight into the problem.
We can see our graph as a tree of BiConnected Components (BCCs).
- The edges of the tree are all bridges.
Let’s define a few things before continuing further.
- The first node of a BCC that is visited in the DFS tree will represent that BCC.
- Let $$$rep[u]$$$ be the representative of the BCC of node $$$u$$$.
- $$$cnt[u]$$$ be the number of edges in the BCC of $$$u$$$.
- Root node of our tree of BCCs is $$$root$$$.
- $$$lca(u, v)$$$ is the lowest common ancestor of $$$u$$$ and $$$v$$$.
With all that set, let us now look at the DFS tree.
We can build an array $$$dp$$$ to store the answer to $$$query(root, u)$$$, for all $$$u$$$, and to answer queries, we can use LCA.
In a typical LCA use case, query(u, v) would be $$$dp[u] + dp[v] - 2 * dp[lca(u, v)]$$$, But is that the case here?
Let us bring attention to a few things.
Is $$$u = rep[u]$$$?
If $$$u = rep[u]$$$, $$$u$$$ is the first vertex of its BCC in the DFS tree. Therefore all the edges in the BCC of $$$u$$$ will not lie in any simple path from $$$u$$$ to $$$root$$$.
Example:
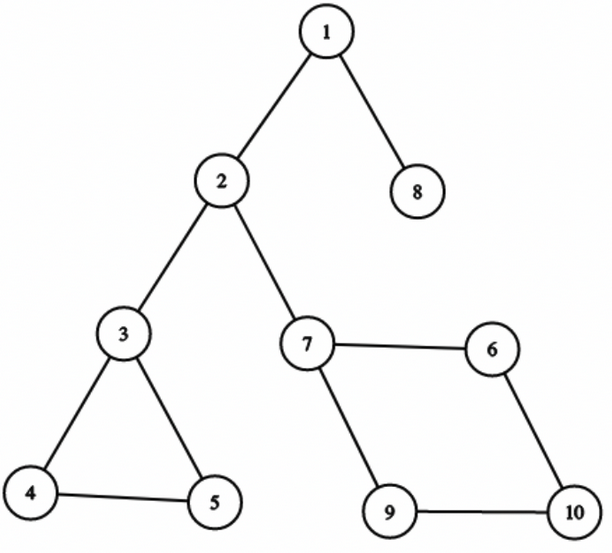
In this graph, Let's say $$$root$$$ is $$$1$$$.
See that, $$$dp[3]$$$ should be $$$0$$$, and $$$dp[4]$$$ should be $$$3$$$. They are in the same BCC, but $$$3$$$ is the topmost node, that is, the representative.
Let $$$p$$$ be the parent of $$$u$$$.
So, to calculate $$$dp[u]$$$,
\begin{align} dp[u] = \begin{cases} dp[p] & \text{if $$$rep[u] = u$$$,}\\dp[rep[u]] + cnt[u] & \text{otherwise} \end{cases} \end{align}
Passing through the representative of a BCC.
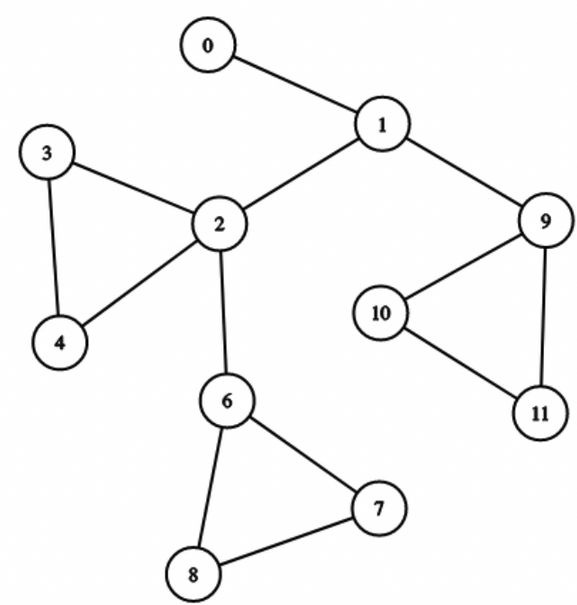
Let's say we have a graph of this type,
Let's choose our $$$root$$$ to be $$$0$$$ and look at node $$$6$$$.
There will be no simple path from $$$root$$$ to $$$6$$$ that uses the edges of the BCC of node $$$2$$$.
Therefore, $$$dp[6]$$$ should not include edges from the BCC of node $$$2$$$. This is already dealt with by our earlier definition of $$$dp[u]$$$!
The cases of $$$query(u, v)$$$.
Now, $$$query(u, v)$$$ depends upon how $$$u$$$ and $$$v$$$ are connected in the graph. These are some significant cases.
Case 1: $$$rep[u] = rep[v]$$$
That is, $$$u$$$ and $$$v$$$ are part of the same BCC. Therefore, the answer to $$$query(u, v)$$$ is just $$$cnt[u]$$$.
Then, we have two cases concerning $$$lca(u, v)$$$.
Case 2.1: We must visit only one node in the BCC of $$$lca(u, v)$$$.
Case 2.2: We must visit at least two nodes in the BCC of $$$lca(u, v)$$$.
Example: $$$u = 6, v = 5$$$
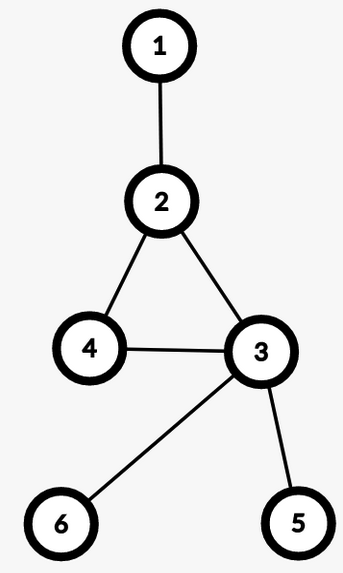

In 2.1, in any simple path from $$$u$$$ to $$$v$$$ we won’t have any edge from the BCC of $$$lca(u, v)$$$. Therefore, we don’t need to include $$$cnt[lca(u, v)]$$$ in the answer. While in 2.2, those edges will be included.
In conclusion, in this setup, we need to determine how the simple paths from $$$u$$$ to $$$v$$$ cross through the BCC of $$$lca(u,v)$$$, then the queries will be answered.
We can use binary lifting to determine which node is the lowest ancestor of $$$u$$$ in the DFS tree that is a part of the BCC of $$$lca(u, v)$$$. Similarly, we can find that node for $$$v$$$.
We can judge which of the above cases any $$$query(u, v)$$$ is based on these two nodes.
There are other ways to distinguish, including using a link-cut tree.
We can create a smart graph to make it so that $$$query(u, v)$$$ is $$$dp[u] + dp[v] - 2 * dp[lca(u, v)] + val[lca(u, v)]$$$, with no casework involved.
We will create virtual nodes representing each BCC. Remove all non-bridges from the graph, and connect all nodes of a BCC to its virtual node.
For example:
 -->
--> 
Here $$$v$$$ is the virtual node, and all the nodes present in BCC of $$$2$$$ are directly connected to the BCC's virtual node.
Let us define the value of each actual node to be $$$0$$$ and every virtual node to be the count of edges of its BCC. Build an array $$$dp$$$ that stores the sum of the values of all vertices from $$$root$$$ to the current node.
You can go back and see how each of the cases would be dealt with by this new graph.










Anyone got the DP solution for D please?
from tourist's submission
lets have
dp[l][r]as number of ways we can construct our array from l to r, with elements[n-(r-l+1)+1, n](basically(r-l+1)of highest distinct elements) regardless of Kthe next element we are gonna put is
n-(r-l+1), so we try to extend out dp to the left and to the right to calculatedp[l-1][r]anddp[l][r+1]. Do not forget to check if the element we put next is valid to restrictons given wth (i, j, x, y)I understood the solution of D that is provided in the editorial. But trying to understand the dp approach for the same. I saw many solved it by dp but not able to get my head around. Please explain anyone.
You can watch neal's video on Youtube. He fills numbers from left and right bounds to inner instead. Because the sequence is "bitonic", values filled must be in increasing order (you climb up to the peak from 2 sides).
So, the same thing goes here: because you are filling from middle toward outer, values filled must be in decreasing order (you go down from the peak).
See my submission: 186149744
Thanks :)
hahaha, just tagging tourist & neal like brothers.
Can you please tell why we always choose "(r-l+1) of highest distinct elements"?
I used a similar DP to tourist's that might be slightly easier to understand. If anyone is interested, check my submission here. I also added some comments that might help in understanding.
Hint for F before the editorial is out:
The provided definition of the given graph,
actually means a cactus graph.no, it doesn't, my bad :facepalm:What are the kind of edges we want to cut if we want to keep the path connected?
We want to cut the edges that lie on a simple cycle.
If we want to decompose a graph into simple cycles, what algorithm do we use?
We use the Biconnected Components algorithm. After using it, the graph of BCCs become a tree. Now we can use LCA/Mo's on trees/whatever algorithm we would use on trees, on this trees of BCCs.
No, it is not true that the definition implies that the graph is a cactus.
Oh, I didn't realize that in the graph given there are no vertex in common between two simple cycles, that's my bad. Do we have a name specifically for this kind of graphs?
A graph where simple cycles share no common vertex is a cactus graph, which is not what is described by the problem's conditions.
Oh, now I saw that it's the set of vertices, not the set of edges. My bad, sorry!
what is a cactus graph
"In graph theory, a cactus (sometimes called a cactus tree) is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, it is a connected graph in which every edge belongs to at most one simple cycle, or (for nontrivial cactus) in which every block (maximal subgraph without a cut-vertex) is an edge or a cycle." — Wikipedia
A connected graph in which no two simple cycles have more than one vertex in common.
How does the validator for F work? I tried the Petersen graph (https://codeforces.com/contest/1763/hacks/878513) and the validator accepted it, but I believe it does not satisfy the condition of the problem statement. Did I input the graph wrong, or is it actually a valid test case?
After some more experimentation, I feel that either I have grossly misunderstood the precondition as described in the problem or the validator is completely inconsistent with that precondition.
Hey, thanks for pointing this out.
The validator for problem F removes bridges and then ensures that all the subgraphs remaining have no articulation points. This is enough to fail all the graphs that will cause solutions to the problem to fail.
The Petersen graph doesn't have a Hamiltonian cycle and thus fails the condition given in the statement but will not fail any solutions or the validator.
Since we cant find Hamiltonian cycles in all the subgraphs efficiently, the validator is made like this. According to the statement, the Petersen graph should fail though, sorry for the confusion.
Do you have any suggestions to improve the validator?
Thanks for the explanation. The condition in the problem statement seems like it might be infeasible to check. Probably the correct thing to do would have been to use a different condition or disallow hacking.
We had wanted to disable hacking but, in the end, thought that this validator would be enough. We were only thinking about the cases that cause solutions to fail and overlooked graphs like these.
Sorry for the inconsistent validator. We will do better next time!
It is possible to allow hacking in these kind of problems. We know that this reduces to largest cycle decomposition, with no intersections, as having two intersecting cycles implies there is larger cycle that contains both. Or in essence, the sum of sizes of all distinct largest cycles of each node is $$$n$$$. Therefore we can require it to be printed alongside the input when hacking. You can set up the problem to be interactive, to allow extra input in the hack alongside the input data.
It would be interesting to have the hack format only available when you solve the problem, because it may serve as too large a hint to the solution.
To verify the correctness of the largest cycle decomposition, you can iterate over all cycles in decreasing order of size. Notice that when you remove the largest cycle, no remaining connected component can have more than 2 edges towards the cycle, as that would imply there exists a strictly larger cycle. Now this implies there is no other cycle going through the largest cycle, so you can simply delete it, and look at the next largest cycle, independent of the nodes and edges of the largest cycle. This amortizes to $$$O(n\log{n})$$$ when implemented using a DSU with roll backs and a map.
For the future, I would recommend all problem-setters to disallow hacking, or either only allow a subset of cases in hacks. It is not reasonable to allow input that does not satisfy the condition of the statement, because it's not guaranteed that every solution uses the same observation, even if it's true for the validator solutions, and may cause your round to be unrated.
I think I have a different way of the checking the validity of the graph.
I'm pretty sure the restriction means that you basically have a cactus (each edge is in at most one cycle), except that the cycles can have spanning chords. So we can construct the block-cut tree of the graph and make sure that all the meta-nodes contain a cycle which only has spanning chords. You can find the cycle with DFS, then make sure all the additional edges in the component are all chords on the cycle.
Please LMK if this check is incorrect.
How can you find the biggest cycle with a dfs? Isn't that the hamiltonian cycle problem, which is NP-complete?
Because this is a special case we can find any cycle with the DFS, then continue finding cycles, and patch them together at the chords. If we have two adjacent cycles that share more than one edge, then we can immediately say this test is invalid.
I thought about implementing this and submitting it to the judge to check if all the tests meet this condition, but it was quite annoying, so I didn't implement it.
Basically we are taking advantage of the structure of the graphs we are looking for making the problem easier I think.
Are you saying to get all of the back edges in the dfs tree and check those? What if you have 1-2-3-4, where 3 and 4 have back edges to 1?
No I'm not saying that.
What I am saying is you find some cycle in this component (any cycle it doesn't matter).
Then you look at the endpoints with some un-visited edges going out, and you DFS again from there, finding another cycle that ends at either of your neighbors in the previous cycle. If you find a cycle that doesn't end at one of your neighbors, then you immediately quit because the graph is invalid; otherwise, you know the edge between you and your neighbor in the previous cycle must be a chord, so you can ignore that edge, and now patch these two cycles together into a single cycle. Now rinse & repeat. The process will terminate in linear time with respect to the size of the component.
Shoot my b, this is NP
I commend you on your efforts to prove P = NP, but this is very very poor.
I suppose this blog may help.
editorials with hints are appreciated:)
Is it rated ? Rating changes are rolled back without notice..
Did you find out why it happened? I'd really like those points back :(
They are removing the cheaters ! :) they will come back
I think it is impossible to write a validator for F. I think that for graphs that are connected enough such that each two vertices share a circle,it is still hard to find whether there exists a hamilton circle.
I think that biconnected graphs are enough to satisfy my condition,and finding a hamilton cycle for such graphs is equivalent with finding one in any graph.
When calculating ifac[i] we can calculating each (fac[i]^(mod-2))%mod individually, with time complexity is O(n*log(mod)), which may cause TLE when n is large. We can just calculate ifac[n]=(fac[n]^(mod-2))%mod, and ifac[i]=ifac[i+1]*(i+1)%mod, where i iterate from n-1 to 0, with complexity O(n+log(mod)), which is reduced to about 1/30.
In problem C, solution, first paragraph, $$$m > l$$$ should be $$$m > r$$$.
Thanks. Fixed it.
On second operation your array would become 0 0 0 :)
Edit: just to elaborate
The operation is applied to the whole subarray. So in your case the array would look like this 4 9 5 -> (1, 3) -> 1 1 1 -> (1, 3) -> 0 0 0
The author seems to be simulating the attacks in problem B, but since health can be up to a billion, couldn't simulating the attacks with a while loop cause TLE? In my case I used the quadratic formula to avoid this problem. What am I missing here?
The problem statement states that $$$0 \le k \le 10^5$$$. The power of each monster is at least $$$1$$$. If there are still some monsters alive, $$$k$$$ will decrease by at least $$$1$$$ every iteration. If $$$k$$$ reaches zero before all monsters die, the answer is "NO". Thus, the loop will run for a maximum of $$$10^5$$$ iterations per test case before $$$k$$$ reaches zero, and since there are at most $$$100$$$ test cases, the loop will run for $$$10^7$$$ iterations in total at maximum, well within the time limit.
Thanks, makes sense.
I like your solution, although more difficult to implement. Could you explain how you come up with it ?
I needed a way to calculate the number of attacks necessary to kill a given monster, but I hadn't noticed the subtlety that vgtcross pointed out, so instead I found a formula for the amount of damage dealt over m attacks, given Genos power level. Then I solved for m such that the damage dealt was equal to the monster's health, h, and took the ceiling of the solution as my number of attacks. Then Genos power level was reduced accordingly and I moved on through the list of monsters.
I think you meant a suffix array there in problem B health solution.
Thanks. Fixed it.
Problem D, Mistake (typo) in first para of solution and spoiler under Hint1.
i′=n−j+1, j′=n−i+1 (Should be +1, not -1, in both places)
Thanks for pointing it out! Will correct it.
Just curious.. How to solve D with the bonus constraints ?
Use binomial formula: sum(C(n,k))=2^n where k=0 to n
You may refer to this comment. A similar approach was also described by satyam343 during testing as well. Hope this helps :)
Thanks a lot !
Thanks for such a amazing round guys :)
I like $$$D$$$ a lot :)
$$$D$$$ can be done entirely without any math--just with dynamic programming.
The first observation is that within a bitonic permutation, the position of the element 1 is either at the beginning of the array or at the end of the array. Likewise, element 2 is either adjacent to element 1 or at one of the endpoints. etc.
So we can imagine constructing our "increasing" beginning part separately than our decreasing ending part.
Say we have the permutation [2, 3, 6, 5, 4, 1].
Start with element 1: [], [1]
................element 2: [2], [1]
................element 3: [2, 3] [1]
................element 4: [2, 3] [4, 1]
................element 5: [2, 3] [5, 4, 1]
................element 6: [2, 3, 6] [5, 4, 1] or [2, 3] [6, 5, 4, 1] (doesn't really matter)
dp[left][right]is the number of ways to construct our sequence if we use only numbers from1...left + right, withleftnumbers in the decreasing part andrightin the increasing part.Transitions are easy:
dp[left][right] += dp[left - 1][right](add something to the left)dp[left][right] += dp[left][right - 1](add something to the right)Now we just have to check to make sure that the index and value matches with $$$i, j, x, y$$$, which can be done easily.
Also permutation has to be bitonic, not strictly increasing/decreasing, so take care of that!!!
Olympia, can you please explain more clearly, what do you mean by (in taking your permutation example), start with element 1, ... With element 2, .... so on ?What are you trying to say , I am not able to get that?
Start placing the elements in increasing order of value. That is, first decide if the element with value 1 is in the "increasing" or "decreasing" half; then decide if the element with value 2 is in the "increasing" or "decreasing" half; then decide if the element with value 3 is in the "increasing" or "decreasing" half; and so on.
As in the example, I started placing elements with value 1, then 2, then 3, then 4, then 5, then 6.
Hi,
A (partial) solution that I could come up with for problem F:
Let $$$x$$$ be some vertex and $$$C$$$ be the largest cycle containing $$$x$$$. By the problem statement, all cycles $$$C'$$$ to which $$$x$$$ belongs to must be a subset of $$$C$$$. Define
.
Also let
Now, I claim that if $$$x$$$ lies on a simple path between any given two nodes $$$a$$$, $$$b$$$, then every $$$e \in \sigma(x)$$$ lies on a simple path between $$$a$$$ and $$$b$$$. Further every such edge is non-critical. (We say an edge $$$e$$$ lying on a simple path between $$$a$$$ and $$$b$$$ is non-critical if $$$G-e$$$ has a path between $$$a$$$ and $$$b$$$.) I do not have a formal proof for this, but you can see this by trying out examples on a piece of paper.
Now we can abstract away the set of vertices contained in each longest cycle as a super node. Each such super node will contain a pointer to the value $$$\tau(x)$$$ where x is any point on the cycle. Further nodes not contained in any cycle can also be considered as supernodes (for simplicity) comprising of just the node itself and having $$$\tau$$$ value as 0.
Any edge in the original graph connecting two largest cycles will be considered as an edge between the two supernodes (corresponding to these largest cycles) in the new graph.
Now the new graph will just be a tree (notice this means it will also be connected). We can store which vertices belong to which supernode in a array. Now given $$$a$$$ and $$$b$$$, we find out the supernode containing $$$a$$$ and $$$b$$$, say $$$A$$$ and $$$B$$$ resp. We just find the sum of $$$\tau$$$ values along the path from $$$A$$$ to $$$B$$$ (including the end points).
This I think can be done in $$$O(1)$$$ (?) through prefix sums. I am not sure how to implement it in a tree, but I am pretty sure it can be done as array prefix sums is just a special case of this.
Please do let me know in case you find a mistake in my reasoning, or wish to improve it.
Thanks!
Sorry for the delay in problem F's editorial. I hope it gives you more to think about!
thanks for sol
For problem E Can anyone explain how for P = 4.
the answer is 5, 6
crimsonred, ...nvm, DreadArceus ?
cant the graph be like this:
which gives answer as 4, 0
Here there are 6 ordered pairs but we need exactly 4.
Pairs:- $$$(1,2), (1,3), (1,4), (2,3), (2,4),(3,4)$$$
Thank you,
I kept thinking (u, v) as a directed edge and completely forgot that ordered pairs were asked.
BTW this will be answer for p = 4?
The p reaches pairs are : (1, 2), (1, 3), (2, 3), (4, 5)
and the unidirectional pairs are : (1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5)
Yes and the directed edge (1,3) is unnecessary.
Linear solution for problem D
C was interesting. At first it looked like another mathematical array problem, but the solution turned out to be simple.
About problem F:
Is the "tree of BiConnected Components" mentioned in the editorial the same as the block-cut tree of the graph? From the description I think it is not, and I think that the solution when using the block-cut tree of the graph is quite similar, but maybe simpler. I also think that when using the block-cut tree, the solution works for any graph, without needing the condition mentioned in the statement. Did anyone do the same? Or could someone explain why the condition in the statement is necessary for the solution to be correct?
You are correct. The block-cut tree solution works for any graph. A few participants did solve it that way.
However, F was not intended to require knowing about block-cut trees. The condition in the statement makes this problem solvable with a few creative ideas as well.
Great, thanks for clarifying. I think it was a good decision to add such condition and make it solvable with other ideas as well :)
in Problem B testcase:
1
2 7
6 8
1 8
should give NO as per online judge, isn't it should give YES
same doubt
after first attack:
H: [0, 1]
K: 7 — 1 = 6
after second attack:
H: [0, 0]
K: 0
all the monsters are killed before k becomes 0. correct me if i'm wrong
UPD:
Ok I got it, K is decreased by the amount of the power of the minimum ALIVE monster. So we don't subtract the power of the first monster after first attack as it will be killed after the attack. So we have to subtract the power of the second which makes K <= 0