1779A - Hall of Fame
Author: n0sk1ll
What happens when $$$\texttt{L}$$$ appears after some $$$\texttt{R}$$$ in the string?
Suppose that there exists an index $$$i$$$ such that $$$s_i = \texttt{R}$$$ and $$$s_{i+1} = \texttt{L}$$$. Lamp $$$i$$$ illuminates trophies $$$i+1,i+2,\ldots n$$$ and lamp $$$i+1$$$ illuminates $$$1,2,\ldots i$$$. We can conclude that all trophies are illuminated if $$$\texttt{L}$$$ appears right after some $$$\texttt{R}$$$. So, strings $$$\texttt{LLRRLL}, \texttt{LRLRLR}, \texttt{RRRLLL}, \ldots$$$ do not require any operations to be performed on them, since they represent configurations of lamps in which all trophies are already illuminated.
Now, we consider the case when such $$$i$$$ does not exist and think about how we can use the operation once. Notice that if $$$\texttt{R}$$$ appears right after some $$$\texttt{L}$$$, an operation can be used to transform $$$\texttt{LR}$$$ into $$$\texttt{RL}$$$, and we have concluded before that all trophies are illuminated in that case. So, if $$$\texttt{LR}$$$ appears in the string, we perform the operation on it.
An edge case is when $$$\texttt{L}$$$ and $$$\texttt{R}$$$ are never adjacent (neither $$$\texttt{LR}$$$ nor $$$\texttt{RL}$$$ appears). Notice that $$$s_i = s_{i+1}$$$ must hold for $$$i=1,2,\ldots n-1$$$ in that case, meaning that $$$\texttt{LL} \ldots \texttt{L}$$$ and $$$\texttt{RR} \ldots \texttt{R}$$$ are the only impossible strings for which the answer is $$$-1$$$.
Solve the task in which $$$q \leq 10^5$$$ range queries are given: for each segment $$$[l,r]$$$ print the required index $$$l \leq i < r$$$, $$$0$$$ or $$$-1$$$.
1779B - MKnez's ConstructiveForces Task
Author: n0sk1ll
There always exists an answer for even $$$n$$$. Can you find it?
There always exists an answer for odd $$$n \geq 5$$$. Can you find it?
If $$$n$$$ is even, the array $$$[-1,1,-1,1, \ldots ,-1,1]$$$ is a solution. The sum of any two adjacent elements is $$$0$$$, as well as the sum of the whole array.
Suppose that $$$n$$$ is odd now. Since $$$s_{i-1} + s_i$$$ and $$$s_i + s_{i+1}$$$ are both equal to the sum of the whole array for each $$$i=2,3,\ldots n-1$$$, it must also hold that $$$s_{i-1} + s_i = s_i + s_{i+1}$$$, which is equivalent to $$$s_{i-1} = s_{i+1}$$$. Let's fix $$$s_1 = a$$$ and $$$s_2 = b$$$. The condition above produces the array $$$s = [a,b,a,b, \ldots a,b,a]$$$ (remember that we consider an odd $$$n$$$).
Let $$$k$$$ be a positive integer such that $$$n = 2k+1$$$. The sum of any two adjacent elements is $$$a+b$$$ and the sum of the whole array is $$$(k+1)a + kb$$$. Since the two values are equal, we can conclude that $$$ka + (k-1)b = 0$$$. $$$a=k-1$$$ and $$$b=-k$$$ produces an answer. But, we must be careful with $$$a=0$$$ and $$$b=0$$$ since that is not allowed. If $$$k=1$$$ then $$$ka+(k-1)b=0$$$ implies $$$ka=0$$$ and $$$a=0$$$, so for $$$n=2\cdot 1 + 1 = 3$$$ an answer does not exist. Otherwise, one can see that $$$a=k-1$$$ and $$$b=-k$$$ will be non-zero, which produces a valid answer. So, the array $$$[k-1, -k, k-1, -k, \ldots, k-1, -k, k-1]$$$ is an answer for $$$k \geq 2$$$ ($$$n \geq 5$$$).
Solve a generalized task with given $$$m$$$ — find an array $$$a_1,a_2, \ldots a_n$$$ ($$$a_i \neq 0$$$) such that $$$a_i + a_{i+1} + \ldots a_{i+m-1}$$$ is equal to the sum of the whole array for each $$$i=1,2,\ldots n-m+1$$$ (or determine that it is impossible to find such array).
1779C - Least Prefix Sum
Author: n0sk1ll
Try a greedy approach.
What data structure supports inserting an element, finding the maximum and erasing the maximum? That is right, a binary heap, or STL priority_queue.
Let $$$p_i = a_1 + a_2 + \ldots a_i$$$ and suppose that $$$p_x < p_m$$$ for some $$$x < m$$$. Let $$$x$$$ be the greatest such integer. Performing an operation to any element in the segment $$$[1,x]$$$ does nothing since $$$p_m - p_x$$$ stays the same. Similarly, performing an operation to any element in segment $$$[m+1,n]$$$ does not affect it.
A greedy idea is to choose the maximal element in segment $$$[x+1,m]$$$ and perform an operation on it, because it decreases $$$p_m$$$ as much as possible. Repeat this process until $$$p_m$$$ eventually becomes less than or equal to $$$p_x$$$. It might happen that a new $$$p_y$$$ such that $$$p_y < p_m$$$ and $$$y<x$$$ emerges. In that case, simply repeat the algorithm until $$$p_m$$$ is less than or equal to any prefix sum in its "left".
Suppose that $$$p_x < p_m$$$ and $$$x > m$$$ now. The idea is the same, choose a minimal element in segment $$$[m+1,x]$$$ and perform an operation on it as it increases $$$p_x$$$ as much as possible. And repeat the algorithm as long as such $$$x$$$ exists.
To implement this, solve the two cases independently. Let's describe the first case as the second one is analogous. Iterate over $$$i$$$ from $$$m$$$ to $$$1$$$ and maintain a priority queue. If $$$p_i < p_m$$$, pop the queue (possibly multiple times) and decrease $$$p_m$$$ accordingly (we simulate performing the "optimal" operations). Notice that one does not have to update any element other than $$$p_m$$$. Add $$$a_i$$$ to the priority queue afterwards.
The time complexity is $$$O(n \log n)$$$.
Solve the task for each $$$m=1,2,\ldots, n$$$ i.e. print $$$n$$$ integers: the minimum number of operations required to make $$$a_1 + a_2 + \ldots a_m$$$ a least prefix sum for each $$$m$$$ (the tasks are independent).
1779D - Boris and His Amazing Haircut
Author: n0sk1ll
If $$$a_i < b_i$$$ for some $$$i$$$, then an answer does not exist since a cut cannot make a hair taller.
If you choose to perform a cut on some segment $$$[l,r]$$$ with a razor of size $$$x$$$, you can "greedily" extend it (decrease $$$l$$$ and increase $$$r$$$) as long as $$$x \geq b_i$$$ for each $$$i$$$ in that segment and still obtain a correct solution.
There exist some data structures (segment tree, dsu, STL maps and sets, $$$\ldots$$$) ideas, but there is also a simple solution with a STL stack.
Consider $$$a_n$$$ and $$$b_n$$$. If $$$b_n$$$ is greater, the answer is NO since it is an impossible case (see "Stupid Hint" section). If $$$a_n$$$ is greater, then a cut on range $$$[l,n]$$$ with a razor of size $$$b_n$$$ has to be performed. Additionally, $$$l$$$ should be as small as possible (see "Hint" section). For each $$$i$$$ in the range, if $$$a_i$$$ becomes exactly equal to $$$b_i$$$, we consider the position $$$i$$$ satisfied. If $$$a_n$$$ and $$$b_n$$$ are equal, then we simply pop both arrays' ends (we ignore those values as they are already satisfied) and we continue our algorithm.
Onto the implementation. We keep track (and count) of each razor size we must use. This can simply be done by putting the corresponding sizes into some container (array or vector) and checking at the end whether it is a subset of $$$x_1,x_2,\ldots x_m$$$ (the input array of allowed razors). To do this, one can use sorting or maps. This part works in $$$O(n \log n + m \log m)$$$ time.
Implementing cuts is more challenging, though. To do this, we keep a monotone stack which represents all cuts which are valid until "now" (more formally, all cuts with their $$$l$$$ being $$$\leq i$$$, and the value of $$$l$$$ will be determined later). The top of the stack will represent the smallest razor, and the size of razors does not decrease as we pop it. So, we pop the stack as long as the top is smaller than $$$b_n$$$ (since performing an operation which makes $$$a_i$$$ less than $$$b_i$$$ is not valid). After this, if the new top is exactly equal to $$$b_n$$$ we can conclude that we have satisfied $$$a_n = b_n$$$ with some previous cut and we simply continue our algorithm. Otherwise, we add $$$b_n$$$ to the stack as a cut must be performed. This part works in $$$O(n + m)$$$ time.
Total complexity is $$$O(n \log n + m \log m)$$$ because of sorting/mapping.
Solve the task in $$$O(n+m)$$$ total complexity.
1779E - Anya's Simultaneous Exhibition
Author: n0sk1ll
A tournament graph is given. Player $$$i$$$ is a candidate master if for every other player there exists a path from $$$i$$$ to them. Can you find one candidate master? (which helps in finding all of them)
Statement: If player $$$i$$$ has the highest out-degree, then they are a candidate master.
Proof: Let's prove a stronger claim, if player $$$i$$$ has the highest out degree, then they reach every other player in $$$1$$$ or $$$2$$$ edges. Let $$$S_1$$$ be the set of players which are immediately reachable and let $$$S_2$$$ be the set of other players (not including $$$i$$$). Choose some $$$x \in S_2$$$. If $$$x$$$ is not reachable from $$$i$$$, then it has an edge to it as well as to every player in $$$S_1$$$, meaning that the out-degree of $$$x$$$ is at least $$$|S_1|+1$$$. This is a contradiction, since $$$i$$$ has out-degree exactly equal to $$$|S_1|$$$ and the initial condition was for $$$i$$$ to have the highest out-degree. So, every $$$x \in S_2$$$ is reachable by $$$i$$$, which proves the lemma.
Statement: There exists an integer $$$w$$$ such that player $$$i$$$ is a candidate master if and only if its out-degree is greater than or equal to $$$w$$$.
Proof: Let $$$S_1, S_2, \ldots S_k$$$ represent the strongly connected components (SCC) of the tournament graph, in the topological order ($$$S_1$$$ is the "highest" component, while $$$S_k$$$ is the "lowest"). Since the graph is a tournament, it holds that there exists a directed edge from $$$x$$$ to $$$y$$$ for each $$$x \in S_i$$$, $$$y \in S_j$$$, $$$i<j$$$. We can also conclude that $$$x$$$ has a higher out-degree than $$$y$$$ for each $$$x \in S_i$$$, $$$y \in S_j$$$, $$$i<j$$$. The same holds for $$$i=1$$$, which proves the lemma since $$$S_1$$$ is the set of candidate masters, and also each player in it has strictly higher out-degree than every other player not in it.
For each player, we host a simul which includes every other player (but themselves). This tells us the necessary out-degrees and we can easily find one candidate master (the one with highest out-degree).
The second step is to sort all players by out-degree in non-increasing order and maintain the current $$$w$$$ described in "Lemma 2". Its initial value is the out-degree of player $$$1$$$. As we iterate over players, we host additional simuls: if player $$$i$$$ wins a match against at least one player among $$$1,2, \ldots j$$$ (the set of current candidate masters), then $$$i$$$ is also a candidate master, as well as $$$j+1, j+2, \ldots i-1$$$, we update the set accordingly and eventually decrease $$$w$$$.
The first step requires $$$n$$$ simuls to be hosted, and the same hold for step $$$2$$$. In total, that is $$$2n$$$ simuls (or slightly less, depending on implementation).
Solve the task if $$$n-1$$$ simuls are allowed to be hosted.
1779F - Xorcerer's Stones
Author: n0sk1ll
If XOR of all stones equals $$$0$$$, then by performing one spell to the root we obtain an answer.
Solve the task for even $$$n$$$.
If $$$n$$$ is even, performing a spell to the root guarantees that all nodes will have the same number of stones, meaning that the total XOR of the tree is $$$0$$$, thus performing the same spell again makes all nodes have $$$0$$$ stones.
Consider even and odd subtrees. What does a spell do to them?
A spell performed to the odd subtree does nothing. It does not change the total XOR, and it also makes performing a spell to some node in its subtree useless as their XORs would be $$$0$$$ anyway. Thus, we are only interested in even subtrees.
Please refer to the hints as steps. Let's finish the casework:
Let nodes $$$u$$$ and $$$v$$$ have even subtrees. And let the spell be performed on $$$u$$$, and then on $$$v$$$ slightly later. Consider the following $$$3$$$ cases:
- $$$u$$$ is an ancestor of $$$v$$$; performing a spell on $$$v$$$ does not make sense as its subtree's XOR is already $$$0$$$.
- $$$v$$$ is an ancestor of $$$u$$$; performing a spell on $$$u$$$ does not make sense either as it will be "eaten" by $$$v$$$ later. More formally, let $$$s_u$$$ be the current XOR of $$$u$$$'s subtree. We define $$$s_v$$$ and $$$s_1$$$ analogously. A spell performed on $$$u$$$ sets $$$s_v := s_v \oplus s_u$$$ and $$$s_1 := s_1 \oplus s_u$$$. Later, the spell performed on $$$v$$$ sets $$$s_1 := s_1 \oplus s_v$$$. Notice that the final state of $$$s_1$$$ is the same as if only the spell on $$$v$$$ was performed (since $$$s_u \oplus s_u = 0$$$). This means that the total XOR stays the same independent of whether we perform a spell on $$$u$$$ or not.
- Neither $$$u$$$ or $$$v$$$ is a parent of the other; this is the only case we are interested in and we will use this as a fact.
We only need to choose some subtrees such that their total XOR is equal to the XOR of the root. Why? Because after applying the spells to them the total XOR becomes $$$0$$$, and that problem has been solved in "Hint 1.1". Of course, each pair of subtrees must satisfy the condition in case $$$3$$$, thus finding the subtrees is possible with dynamic programming and reconstruction. In each node we keep an array of size $$$32$$$ which tells us the possible XOR values obtained by performing spells on nodes in its subtree. Transitions are done for each edge, from child to parent, in similar fashion to the knapsack problem, but with XOR instead of sums.
Time complexity is $$$O(n A^2)$$$ and memory complexity is $$$O(nA)$$$. It is possible to optimize this, but not necessary.
Can you minimize the number of operations?
The number of them is $$$\leq 6$$$ (in an optimal case).
1779G - The Game of the Century
Author: Giove
Consider the sides of the big triangle. If they have the same orientation (clockwise or counter-clockwise), $$$0$$$ segments have to be inverted since the village is already biconnected.
If the three sides do not all have the same orientation, inverting some segments is necessary. The following picture represents them (or rather, one case, but every other is analogous).
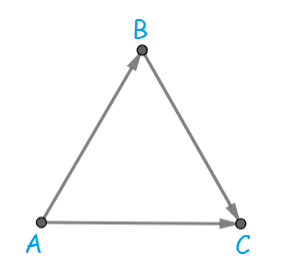
There are two "major" paths:
- $$$A \rightarrow C$$$
- $$$A \rightarrow B \rightarrow C$$$
Each road has a "beginning" in one of the paths, hence it is possible to reach every intersection from $$$A$$$. Similarly, $$$C$$$ can be reached from every other intersection. The problem is that $$$C$$$ acts as a tap as it cannot reach anything.
To make the village biconnected, we will make it possible for $$$C$$$ to reach $$$A$$$ by inverting the smallest number of road segments. Intuitively, that will work since for every intersection $$$x$$$ there exists a cycle $$$A \rightarrow x \rightarrow C \rightarrow A$$$. A formal proof is given at the end of this section.
The task is to find a shortest path from $$$C$$$ to $$$A$$$, with edges having weights of $$$0$$$ (its direction is already as desired) and $$$1$$$ (that edge has to be inverted). To implement this in $$$O(n)$$$, one has to notice that we are only interested in the closest road of each direction to the big triangle's side. One can prove that by geometrically looking at the strongly connected components, and maybe some casework is required. But, the implementation is free of boring casework.
Now, it is possible to build a graph with vertices which belong to at least one of the $$$6$$$ roads we take into consideration (there are $$$3$$$ pairs of opposite directions). One can run a $$$0$$$-$$$1$$$ BFS and obtain the shortest path.
This will indeed make the village biconnected as a shortest path does not actually pass through sides $$$A \rightarrow B$$$ and $$$B \rightarrow C$$$ (why would it? it is not optimal making effort to reach it just to invert some unnecessary additional road segments) The shortest path from $$$C$$$ to $$$A$$$ intersects the side $$$A \rightarrow C$$$ though (possibly multiple times), but it can be proved that every intersection on it is reachable from $$$C$$$. Also, sides $$$A \rightarrow B$$$ and $$$B \rightarrow C$$$ are reachable from $$$C$$$ since $$$A$$$ is reachable from $$$C$$$. This means that all sides are reachable by both $$$A$$$ and $$$C$$$, and so is every other intersection.
Solve the problem if it is required to process $$$q \leq 10^5$$$ queries: invert a given road (and every segment in it), then print the minimum number of road segments you need to additionally invert to make the village biconnected (and not perform them, they are independent from the queries).
1779H - Olympic Team Building
Author: n0sk1ll
Huge thanks to dario2994 for helping me solve and prepare this problem.
Try reversing the process.
Start with some multiset $$${ x }$$$ containing only $$$1$$$ element. We will try to make $$$x$$$ an absolute winner. Extend it by repeatedly adding subsets of equal sizes to it (which have sum less than or equal to the current one).
A simple greedy solution is to always extend the current subset with the one which has the maximum sum. This, however, gives WA as 100 100 101 98 89 103 103 104 111 680 1 1 1 1 1 2 is a counter-example. (see it for yourself!)
Statement: If it is possible to extend some multiset $$$A$$$ to the whole array $$$s$$$, we consider it winning. If $$$A \leq B$$$ holds for some subset $$$B$$$, then $$$B$$$ is also winning. Here, $$$A \leq B$$$ means that there exists a bijection $$$f\colon A\to B$$$ such that $$$x \leq f(x)$$$ for each $$$x \in A$$$.
Proof: Let $$$A, A_1, A_2, \ldots A_k$$$ be a winning sequence of extensions. By definition of $$$A \leq B$$$, we can swap each element of $$$A$$$ with some other element. There are three cases:
- If we swap some $$$x \in A$$$ with an element which is already in $$$A$$$, nothing happens.
- If we swap some $$$x \in A$$$ with an element which is not in any $$$A_i$$$, the sum of $$$A$$$ increases hence it is also winning.
- If we swap some $$$x \in A$$$ with an element which is contained in some $$$A_i$$$, the sum of $$$A$$$ increases, the sum of $$$A_i$$$ decreases and the sum of sums of $$$A,A_1, \ldots, A_i$$$ stays the same. The sequence remains winning.
Special cases of the lemma are subsets of size $$$1$$$. We can conclude that if $$$x$$$ is winning and $$$x \leq y$$$, then so is $$$y$$$. The answer is binary-searchable. Let's work with some fixed $$$s_i = x$$$ from now on. The idea is to maintain a list of current possible winning subsets. The motivation of lemma is to exclude subsets which cannot produce the answer.
we can see that $$${ s_j, s_i } \leq { s_{i-1},s_i }$$$ for each $$$j < i-1$$$, hence the only interesting subset is $$${ s_{i-1}, s_i }$$$ (we excluded others because if one of them is an answer, then so is $$${ s_{i-1}, s_i }$$$. We will use this without explanation later on).
we extend $$${ s_{i-1}, s_{i} }$$$ further to a subset of size $$$4$$$. There will be at most $$$15$$$ new subsets and it can be proved by using the lemma and two pointers.
extend the current subsets to have size $$$8$$$. And, of course, use the lemma again and exclude unnecessary subsets. Implementing it properly should be fast enough. A fact is that there will be at most $$$8000$$$ subsets we have to consider. Although, proving it is not trivial. Consider all subsets of size $$$4$$$ and a partial ordering of them. In our algorithm we have excluded all subsets with large sum and then we excluded all subsets which are less than some other included set. So, the max collection of such subsets is less in size than the max antichain of $$$4$$$-subsets with respect to $$$\leq$$$. Following the theory, a max anti-chain can have size at most $$$\max\limits_{k} f(k)$$$, where $$$f(k)$$$ is the number of $$$4$$$-subsets with indices having sum exactly $$$k$$$. Hard-coding this gives us an approximation of $$$519$$$. This value should be multiplied by $$$15$$$, since we had that many $$$4$$$-subsets to begin with. This is less than $$$8000$$$, which is relatively small.
Extending the $$$8$$$-subsets further sounds like an impossible task. But, greedy finally comes in handy. Every $$$8$$$-subset should be extended with another $$$8$$$-subset which maximizes the sum. It is not hard to see that if an answer exists, then this produces a correct answer too. We are left with solving $$$8$$$-sum in an array of size $$$24$$$. As we need to do this around $$$8000$$$ times, we use the meet in the middle approach. It can be done in around $$$2^{12}$$$ operations if merge sort is used (it spares us the "$$$12$$$" factor in $$$12 \cdot 2^{12}$$$).
Summary: Solving the task for $$$n\leq 16$$$ is trivial. Let's fix $$$n=32$$$. Calculating the exact complexity does not make much sense as $$$n$$$ is fixed, but we will calculate the rough number of basic arithmetic operations used. Firstly, a binary search is used, which is $$$\log 32 = 5$$$ operations. Then, we generate $$$8$$$-subsets which can be implemented quickly (but is not trivial). The meet in the middle part consumes $$$8000 \cdot 2^{12}$$$ operations. The total number of operations is roughly $$$5 \cdot 8000 \cdot 4096 = 163\,840\,000$$$, which gives us a decent upper bound.
Try to construct a strong test against fake greedy solutions :)










very fast tutorial ;)
very fast comment
very fast reply
all of you very fast
very fast seen
not me :(
very very fast
late reply to something very fast
very fast late reply
very fast seen the very fast late reply
Very last reply! Now stop!!
very fast swipe....!!
very fast stuff
fast reply on same level
very fast downvoted
.
very late reply
Is this the fastest published editorial?
These are, as of now, surely the best CF problems of 2023!
F is very similar to : THis Problem
I want to know in Prob.A when I was submitting like for LR the answer is 1, why its wrong?
Since only 1 operation will be enough in this case if we find an "LR" occurence we can just swap it and it's done
I know this too I just want to know that why it's not 1 but i+1. Only 1 can do the work or not?
Consider the case: RRRLLR. If you intended to swap index 1 (or the 0th index), you fail to illuminate the trophy since index 1 and 2 are the same. Obviously, 'L' and 'R' are not fixed at index 1, so outputting 1 will be unreasonable.
I am so stupid I didn't read it right I thought it said to input the operation .
So stupiddddddddddd of me!!!!!!!!!!
Queue forces on C and D
my sol for C was basically to do some math. Starting at m you check all the contiguous sums down from m and up from m. For the sums on the left, they have to be less than or equal to 0 and for the sums on the right, they have to be greater than or equal to 0
Did anyone use a similar approach that worked? I got a WA on pretest 2.
Edit: So I looked at the editorial and while I'm still not clear on the solution, its helped. However, can someone poke holes at my logic here? I manipulated the inequality for cases where k was smaller than m and for cases where k was larger than m. When you do that, you get the following inequalities:
Case 1: (k < m) a_k+1 + a_k+2 + a_k+3 + . . . + a_m <= 0
Case 2: (k > m) a_m+1 + a_m+2 + a_m+3 + . . . + a_k >= 0
So for the first case, you get these inequalities that I've numbered on the left
(1) a_m <= 0
(2) a_m + a_m-1 <= 0
(3) a_m + a_m-1 + a_m-2 <= 0
(m-1) a_m + a_m-1 + a_m-2 + . . . + a_2 <= 0
For the second case, you get these inequalities that I've numbered on the left
(1) a_m+1 >= 0
(2) a_m+1 + a_m+2 >= 0
(3) a_m+1 + a_m+2 + a_m+3 >= 0
(n-m) a_m+1 + a_m+2 + a_m+3 + . . . + a_n >= 0
So I assumed that as long as you solved these cases independently and in order, you would get the optimal answer (go through inequalities numbered 1 through m-1 in case 1, and then go through the inequalities numbered 1 through n-m in case 2.
For the sums on the left, you must iterate till i > 0, not i >= 0. Had made the same mistake at first. AC code: https://codeforces.com/contest/1779/submission/187800612
I did do this in 187817105 though
I did the same thing, we are not considering the maximum number from each subarray, I don't know why we should take that though in the pq
How then would you find the max when you need it?
As explained in the editorial you need to choose such element to perform operations on that causes our target prefix sum to decrease as much as possible. Current element i.e. $$$arr[i]$$$ will not always be that element.
Could you help provide a test case that showcase why it is necessary? Thanks in advance!
did this because I assumed n == 1 is a special case :/
But Why?
Thank you for your code.I got it now. :)
hey! , can you explain the reason for making i>0 instead? I was also making the same mistake but I didn't get why it doesn't work.
If you are still not clear, consider the inequalities a_m+1 + a_m+2>=0, let say they are 4 and -4 respectively, so techincally you dont need to change anything and now lets the next inequality , let a_m+3 be -2 so, now the sum is <0 , so you must change some elements, which will you prefer to change -2 or -4, obviously -4 since it contributes more to the positive sum, thats why you need to keep a priority queue or set for this purpose
Thanks so much! That test case is pretty eye-opening.
Your approach is right! You have to consider one more thing.
Case 1: (k < m) a_k+1 + a_k+2 + a_k+3 + . . . + a_m <= 0
In this case, there can be u and v (u > v) such that, a_u + a_u+1 + . . . + a_m-1 + a_m <= 0 will hold, but a_v + . . . + a_u + a_u+1 + . . . + a_m-1 + a_m > 0
Here, I think you are changing the sign of a_v. What if a_u > a_v?
Changing the sign of a_u will be more significant than changing the sign of a_v.
I think your algorithm changes the sign of a_u instead of a_v!
Think what will happen. You will find the error. Your approach is correct. I got the correct verdict from your approach.
Thanks for the comment! That was the problem I had lol. This was a really educational C!
Why is this solution to C wrong? 187783695
you are storing all the elements at first and then trying to compute the number of operations this doesn't take into consideration that a element at index X s.t. X<M would have the choices of only the elements in range (X,M] for negating in order to make any relative change to the values. .
please see this for reference: https://youtu.be/kzCF4qpsjWQ let me know if you need further help :)
Take a look at Ticket 16656 from CF Stress for a counter example.
Could someone help? Why I got runtime 187832356
wow, so fast!
super fast
E is brilliant!
submitted editorial in 0ms
Damn, B was very sneaky! Great problems!
I messed up the maths once and kept wondering why is the solution wrong :P
Bonus for E (hopefully it's correct :)) Let's find outdegree for all people, call it deg[i]. It's sufficient to find minmum R such that there exists subset of people of size R such that their sum of outdegrees equals nCr(R, 2) + R * (N — R). I was thinking about this during contest but how do you implement it if you want to recover answer as well?? I mean can you do this faster than O(N^4), and in particular in better space complexity?
Btw amazing problemset.
i used same logic. here is my submission. https://codeforces.com/contest/1779/submission/187825157
Wow, I'm so stupid. Obviously this is not equivalent to knapsack, since the answer always consists of some prefix of biggest outdegree guys...
My first contest in my life and the first contest in 2023
For problem F, the editorial says "Time complexity is $$$O(n.A^2)$$$ and memory complexity is $$$O(nA)$$$. It is possible to optimize this, but not necessary". I believe my code has the same complexity as said above but it got TLE at test 10 :( 187833020
Never mind, I figured it out. Because of vector assignment(s).
The way you meet the New Year is the way you live the whole year: that fast editorial for all 2023 contests :)
The n = 3 case in B was really terrifying.
You could have derived it. check here — https://youtu.be/2L326KCBqug ,but yes it gave a feeling that for odds answer would be NO :P!
Why did we look for i > j in problem E (lemma 2)? It seemed to me that i < j should. If I'm wrong, please explain why.
Sorry for my poor English
You are right! $$$i<j$$$ should have been written. Thank you for pointing it out, I fixed it now.
FST is not a funny joke.
About E:
Interactive problems takes a lot time to test the sample of it , so I submit it with out testing the sample .
My program WA on pretest 2 , but pretest 2 is a sample and I don't think this should be deducted from the score .
If there many samples , and I get WA on 2 , in codefoeces's rules , should my score be deducted ? Is this a mistake ?
I don't know , TAT.
(My English is so bad.)
And I think E is a good problem . But many people solve it with mindless guessing.
What sort of mindless guessing?
Only the first pretest is penalty-free, as per the rules.
I think that the author should swap E and F, it's so confusing.
Bonus problems. Yeah !!!
Potatohead orz
I even cannot come up with the lemma 1 of problem E during the contest. Perhaps I've forgotten the knowledge of the Graph Theory I've learned.
Bonus E :
View the match where player $$$u$$$ beat player $$$v$$$ as a directed edge from node $$$u$$$ to $$$v$$$ in a complete graph of $$$N$$$ vertices. Candidate masters are nodes that can be visited from all other nodes through some simple path (in other words, there exist a series of matches(=edges) to disqualify all other players).
All possible candidate masters are the nodes located in the last/terminal Strongly Connected Component(SCC) (SCC that doesnt have any outgoing edge to another SCC). As the graph is complete, this terminal SCC is unique.
For each node, find its outdegree. For the first $$$N-1$$$ nodes, do a simuls againts all other node(player) and count each of their loss match, with a total of $$$N-1$$$ queries. For the final node, calculate its outdegree from the remaining out/in-going edges from the previous $$$N-1$$$ nodes.
The terminal SCC (the candidate masters) are composed of the $$$x$$$ nodes with smallest outdegree such that their sum is equal to the number of edges among those $$$x$$$ nodes $$$=\frac{x(x-1)}{2}$$$. Pick minimum such $$$x$$$.
Report this cheater
Very fast tutorial and Bonus Problems are really interesting
I don't know why this solution gets AC while it shouldn't (Problem D)
187838626
i used sparse table for RMQ but i forgot to initialize the logs array but it passed with no problem!
What will be generalized approach for Problem B bonus part ?
Bonus task for B:
Let n = km + r where 0 <= r <= m-1. Similar with original problem we get (k-1)s_m+s_r=0, where s_m = a1 + a2 + ... + am. When k = 1, r = 1, there's no solution because in this case a1 = s_1 = 0. Otherwise there exist some { a1, a2, ..., am } satisfy the condition. We let ai = a_(i-1)%m+1 for 1 <= i <= n and get a solution.
How did you get the ai = a_(i-1)%m + 1 part?
For rank1 to rank4, all of them got "wrong answer on pretest 2" at B for one time.
What a great problem!
I used vector in the iteration of F, and get stack overflow(maybe in fact MLE?) in the system test. Can anyone explain the reason? Thank you.
As a candidate master, I even CANNOT solve the problem E which is about finding "candidate master".
Why in problem C we are going till i>=1 and not i>=0?
Baltic's favorite number is m, and he wants a1+a2+⋯+am to be the smallest of all non-empty prefix sums.
"non-empty" means there's no need for p0 >= pm
Even though I liked problem E myself, it felt weird that it was interactive, and not just giving degrees for each vertice, and asking the same. Can someone explain to me the reason it was given in such a way?
Because red herrings make for
cruelfunny problems I suppose.But if they give you the degree, It became easier, because you knew that you need the out degree to solve the problem. But in problem E, you maybe think of other paths instead of asking the out degree. (Mistake path came from weaker players like me awa)
anyone can explain this??
Since the two values are equal, we can conclude that ka+(k−1)b=0. a=k−1 and b=−k produces an answer
they have performed mathematical operations and resolved it ... you might find this helpful : https://www.youtube.com/watch?v=2L326KCBqug&t=4s
happy coding :)
In problem b you can have two cases when n is even and when even is odd, this is how we derive the solution for both cases.
case 1: n is even:->
let the total sum of the array be s then a1+a2+....+an=s, and we also know that a1+a2=s and a3+a4=s and so on, therefore we get the equation, s*(n/2)=s.
Now since n can not be 0 we conclude that s has to be 0,so the array looks something like
[x -x x -x....x -x].
case 2: n is odd:->
let the total sum of the array be s then a1+a2+....+an=s, now we already know what we have to do when n is even therefore it makes sense to divide the array as 1(odd part)+(n-1)(even part), now we can extend the idea of case 1 for a2 to an, so we know that a2+a3=s, a4+a5=s and so on.. therefore the equation becomes a1+(n/2)*s=s, and we also know that a1+a2=s.
Solving these two linear equations we get a1=s*(1-(n/2)) and a2=(n/2)*s, for simplicity i took s as 1. so the array looks something like:
[(1-n/2) (n/2) (1-n/2) (n/2).....(1-n/2) (n/2)]
here is my implementation of the problem: https://codeforces.com/contest/1779/submission/187770011
so....what if n/2 bigger than 5000?
see the range of n mate, it is upto 1000, and also i took s as 1 for that purpose.
Alternative explanation for Div2D.
Observation 1: If $$$a_i<b_i$$$ for any $$$i$$$, then the answer is NO.
So we may assume WLOG that $$$a_i \geq b_i$$$ for all $$$i$$$.
Observation 2: We can restrict to using scissors in descending order of $$$x_1 \geq x_2 \geq ... \geq x_n$$$ (i.e use taller scissors first, then go down in size). This is because if there is a solution using another order (not descending), then the same solution intervals but sorted in descending order of the scissors length is still a feasible solution.
Observation 3: We need a scissors of length $$$b[i]$$$ to cut index $$$i$$$.
Notation: For index i, let $$$nx_i$$$ denote the next index after $$$i$$$ such that $$$b[nx_i] > b[i]$$$ (i.e next bigger element in $$$b$$$). This can be preprocessed using a monotonic stack. This is a standard problem so I'll skip the details, but I'll assume you can precompute $$$nx_i$$$ for all $$$i$$$ in $$$O(n)$$$ time. See https://leetcode.com/problems/next-greater-element-ii/ for example.
I'll also treat $$$b$$$ as a set using $$$v\in b$$$ to denote a value in the array $$$b$$$.
For each $$$v \in b$$$, let $$$indices[v]={u_1, ..., u_k }$$$ be a set of all the indices with value $$$v$$$: $$$b[u_j]=v$$$. We can divide $$$indices[v]$$$ into "slots" $$$[u_1, u_2, ..., u_{i_1} ], [u_{i_1+1},..., u_{i_2}],..., [u_{i_r+1}, ..., u_{k}]$$$ where each slot is separated by an element with $$$b$$$ value greater than $$$v$$$. For example, first slot separated from second by $$$nx_{u_1}$$$, and so on.
This means that the interval for scissor with length $$$v$$$ cannot cross the slots in $$$indices[v]$$$.
Now we proceed greedily. If $$$x_i \not\in b$$$, then there is no point using $$$x_i$$$, so skip it.
If $$$x_i \in b$$$, then we look at $$$indices[x_i]$$$. Take the smallest index $$$i_{\min}\in indices[x_i]$$$, and let $$$j_{\max}=nx_{i_{\min}}$$$. We trim all the indices in $$$indices[x_i]$$$ in the range $$$[i_{\min}, j_{\max})$$$ by repeatedly removing the smallest index until the slot is entirely trimmed. Some care should be taken if $$$a_{i_{\min}}=b_{i_{\min}}$$$ since we can skip this index (without starting a new slot).
And that's it, in the end, we check if $$$a_i=b_i$$$ after all the trimming. If it is, we return true, otherwise False.
C++ Implementation Details: $$$indices[v]$$$ is implemented as a map from int (value of $$$b$$$) to set where $$$indices[v]$$$ contains all the indices with value $$$v$$$ in $$$b$$$.
Code: https://codeforces.com/contest/1779/submission/187842280
Can someone please explain lemma 2 of problem E in more simple words. I don’t get why degree of every vertex in Si will be higher than Sj for (i<j).Also why S1 is set of candidate masters.
i may sound a fool or someone who have less knowledge but in problem H cant we just do :
sort the array ( not the original but make another array that have same elements )
Then we have the sorted array , so 1...n/2 elements we will put in an array namely smallelements(lets say), and next n/2+1...n elements in an array namely largeelements(lets say)
Then with repsect to original array we will check that whether a[i] is present in which array (smallelments or largeelements)... if a[i] is in smallelements we will print '0' else if a[i] is in largeelements we will print 1.
FOR THE CASES WHERE DISTINCT ELEMENTS ARE JUST '1' we will simply print 1 for n times
Why would you think that it's correct?
i am not saying this is correct, but i am asking to correct my thinking
An easy way to see why it's incorrect is 1 2 3 10.
There is simply nothing correct in your solution(except that the answer is all 1s if the elements are all equal). I'm really confused by how you came up with that solution.
Because the problem H is designed for LGMs, so if someone is not, their approach will be very likely wrong.
Update: wtf downvote???
Update2: It's awful to get downvoted but don't know why...
Fast & perfect editorial
This contest was probably not good for #1 tourist
That moment when you realize all that time you were trying to solve a version of $$$E$$$ where in each game only $$$1$$$ player is chosen and the other is the winner of the previous game.
More and more vegetable,what should I do?
I had great difficulty in C.
My idea was to use Segment tree but I WA on 2 many times. (Who can help to hack me? Please)
The Segment Tree includes the maxinum and the mininum of each section.
First, Reverse traversal [1~m-1].
s1 = 0
if sum[i] < sum[m] — s1:
s1 = s1 + 2 * query_max{a_i+1~m}
update(the location of the maxinum, -maxinum)
Then, traversal [m+1~n].
s2 = 0
if sum[i] + s2 < sum[m]:
s2 = s2 — 2 * query_min{a_m+1~n}
update(the location of the mininum, -mininum)
Please help.... QWQ
will there be a tutorial for bonus problem :")
jiangly fanbase strong
can anyone please tell me where my solution is wrong:
https://codeforces.com/contest/1779/submission/187871735
Thanks in advance
Edit: nvmi.. i was stupid
Bonus F: After using the hint 6, you will find that this problem equals to choosing some non intersecting subtrees and make them have an xor sum of $$$s$$$. After you get a solution using whatever way (not neccessary with <=6 operations), you can make it within 6 steps using this simple trick about xor vector basis, and you will find that if it is possible to do so, you will always get an answer with less than $$$\log v+1$$$ steps.
Really appreciate that there is a 'bonus' for every problem, and can keep me think deeper about those interesting problems:)
n0sk1ll, any insights on how you implemented the adaptive checker for E?
Usually, adaptive jury is implemented by fixing some invariant in the input. In this one, I fixed the whole tournament graph, but allowed permutations (i.e. the resulting graph after all participants' queries have been asked will be isomorphic to the jury's initially intended one). Jury permutes the graph in a way such that the newly asked vertices will always have the smallest possible (available) out-degree, meaning that there is practically no information about the winners before $$$n-1$$$ queries are asked.
In fact, there exists a solution which uses exactly $$$n-1$$$ queries — the tests seem to be strong. (and in practice, all fake solutions fail to squeeze into $$$2n$$$ queries, which was the constraint in the problem)
Yeah, I always wondered how adaptive interactors are written. It seems an impressive idea to always have smallest possible out-degree during interaction.
Thanks a lot for sharing!
I passed problem H with the following fix of the fake greedy:
While expanding from size 2 to size 4, we enumerate all the 15 ways instead of using greedy.
I don't know if it's correct or not. Can anyone prove its correctness or come up with a counterexample?
My intuition suggests that this is wrong, but I also see why it may be hard to construct a counter test.
n0sk1ll: Do you know how to construct a hack?
My intuition tells me that one should still check at least $$$50\,000$$$ subsets (in a greedy solution), and that there exist counter-tests. Although, I don't have a particular hack.
In Problem E Lemma 2,
We can also conclude that x has a higher out-degree than y for each x∈Si, y∈Sj, i<j.How are we able to conclude this?
Please someone explain this
Because for every pair (i,j) (i<j) all players in Si beat all players in Sj. If that was not the case, then Si and Sj would be the same SCC.
Anyone have solution Bonus Problem for C ?
1779D in second hint, I think it will be x >= bi
$$$x \geq b_i$$$ is correct, I fixed it now :)
How did some people used DSU in solving D ? Example jiangly
Can anybody explain me D problem solution using segment trees???
I solved it using segment tree 187802839. The only purpose of the segment tree is to be able to calculate the maximum element of b in the range [l, r).
I'll try to explain my solution.
Now the only thing is that when we make a cut using razor x on the interval [l, r), there must not be any element of b in the range [l, r) such that b[i] > x. If there exist such b[i] > x, we will cut short i to length x < b[i] which can not be grown back.
A conclusion from above is that maximum element of b in range [l, r) must be <= x. To find the maximum element of b in range [l, r) in O(log n) time, we use a segment tree. A even better data structure to use is a sparse table which can return the maximum of a range in O(1).
All I do is store in a map, razor of which length will have to cut which indices. And then I try to distribute the ranges among all razors available of that length.
Why is my Seg tree implementation giving WA? can you please debug?
https://codeforces.com/contest/1779/submission/187831216
About problem H, I have two questions:
Make all (reachable) big subsets intersect. I used different strategies, the simplest of which is generating $$$15$$$ numbers close to each other by value. There will be $$$\binom{15}{8} = 6425$$$ different subsets, all having similar value, and all are intersecting. Fill the rest of the array in a way such that the "smallest" subset can be extended into a full solution, but others cannot. In practice, more than $$$1000$$$ subsets would have to be considered in any solution.
Write two pointers instead of binary search. As for sorting, It is possible to sort all subsets of an array of length $$$n$$$ in $$$O(2^n)$$$. Consider that all subsets of some prefix $$$a_1, a_2, \ldots a_i$$$ are already sorted, let their array be $$$b_1,b_2,\ldots b_k$$$ where $$$k=2^i$$$, and let $$$x = a_{i+1}$$$ be the new element we consider. The new subsets we add will have sums $$$b_1+x, b_2+x, \ldots b_k+x$$$, and in that order since $$$b$$$ is sorted from previous steps. We only need to merge two already sorted arrays, which is possible in $$$O(k)$$$.
Can anyone explain how non-intersecting subtrees can be ensured in problem F?
I love these bounce problems thank you for the good contest (。♡‿♡。)
nvm
I solved problem D all by myself (after the contest of course) using a monotonic stack approach. I have no one to share it with but I feel happy because that's probably the most challenging problem I've solved with no hints
In problem C, I'm wondering why moving from right to left is correct than moving from left to right
We have a simple way to solve E with $$$n$$$ querys, and to be skipped.
My submission: 187829528 and the one coincides with mine: 187788613.
The code is short and simple so it is easy to be close with others without leaking I think.
So how can I complain for this. :(
Anyone mind to post the solution for E's bonus problem?
Thanks in advance
In F, I have a solution in mind for finding if it is possible to get xor=0 but how to restore the steps is what I can't figure out. I would love it if someone could help. Thankyou
What does "we are only interested in the closest road of each direction to the big triangle's side" means in G's solution? More specifically, what does the "closet road of each direction" means?
same question here. The expression is so confusing and suprisingly there are not much people talking about it.
Why this Seg tree implementation of D is giving WA?? https://codeforces.com/contest/1779/submission/187831216
Problem G's solution is very confusing. Maybe too obvious to explain the meaning of "closest road to the big triangle's side"?
Solved it. "closest road to the big triangle's side" refer to the closest road that is parallel with the corresponding big triangle's side. And the proving is fun, it only takes me about 3 hours of my sleep to do the "case works"
For everyone struggling with H's TLE, here's a little something too TRIVIAL for the solution to mention: just ignore all the cases of which sum is lower than (S * k / 32) (k is the number of elements of the case and S is the total sum of all elements). Pretty TRIVIAL right? Works like magic(at least for me 1000ms -> 100ms) and here's the code (In Java)190213361 btw since it only takes less than 10% of the TL, it makes you wonder what will happen if you replace some of the techs with brute force.
Can someone help me in F? It is clear that if we can find 2 non intersecting even subtrees whose XOR sum is XOR sum of all nodes, then we can solve the problem. But why is this condition necessary?
202603354 Can anyone tell me why this submission for problem D fails for test 2?
Take a look at Ticket 16850 from CF Stress for a counter example.
How can i solve this problem using DSU ??
Why did I have this code title? Help!!
Problem D
n0sk1ll Regarding D, don't understand in editorial, why we need to keep l small as much as possible.
I used monotonic stack and I have kept l as long as possible unless it affects any B[i] such that razer < B[i].
https://codeforces.com/contest/1779/submission/237616405