Sorry for my poor English. If you find a mistake, write me a private message, I'll fix it. Some problems have not been translated yet, now you can try to read the Russian version of editorial with Google Translate.
In this problem you were to find waiting the time for every queue by summing up the purchases of all the people, and return the minimum.
In this problem it is necessary to find the garland with the maximal length, which can be composed of elements that we have.
First, if you need some color, but you don't have it, then the answer is -1
Otherwise, answer is always exists.
Let's sum the answers for all the colors separately.
Suppose we have a pieces of a garland of some color, and we need b pieces. Then we have to add min(a, b) to the answer: if a > = b we will use b 1 meter pieces, in the other case if a < b we will use all a pieces.
In this problem you have to locate the right triangle with cathetuses a, b on a plane with its vertices in integer points.
If the required layout exists, then cathetus a always can be represented as a vector with integer coordinates A{x;y}, and a2 = x2 + y2. Iterate over all possible x (1 ≤ x ≤ a - 1), check, that y = sqrt(a2 - x2) is integer.
Vector, ortogonal to vector {x;y}, is { - y;x}. Take vector B{ - y / g;x / g}, where g = gcd(x, y). The triangle can be located on the plane if and only if b % |B| = 0, where |B| — length of vector B. The candidate for the answer — triangle (0;0)(x;y)( - y / g * b / |B|;x / g * b / |B|), but don't forget about checking that the hypotenuse isn't parallel to coordinate axes.
In this problem you had to simulate route of character in graph.
Note that if you are in vertice i, then edges in all vertices with numbers less than i are turned to pi. It gives us opportunity to see a recurrence formula: let dpi be number of steps, needed to get from vertice 1 to vertice i, if all edges are rotated back, into pi. Then dpi + 1 = 2dpi + 2 - dppi. Answer will be dpn + 1.
BONUS: Can you solve this task without statement pi ≤ i? I don't know the solution, it seems difficult.
In this problem you had to find how to add binomial coefficients in array offline.
Let's see, how problem changes due to increasing k from small to big values.
1) All queries have K = 0
Every time you add 1 on subsegment.
For solve this task you can add 1 at some array b[] in b[L] 1, then substract 1 from b[R+1], and after doing all queries make array a[] as array of prefix sums of array b[].
2) All queries have K = 1
Arithmetic progression 1 2 3 4 ... is added on subsegment
For solve this task you can add 1 at some array c[] in c[L] 1, then substract 1 from c[R+1], and after doing all queries make array b[] as array of prefix sums of array c[]. Actually you added 1 1 ... 1 on every subsegment at each query. If you will substract (R — L + 1) from c[R+1], and make array a[] as array of prefix sums of array b[], then it will be an answer: 1 1 ... 1 became 1 2 3 ... (R-L+1).
3) K is arbitrary
Summaring previous results one can see that if we will do
- a[K+1][L] += 1
- a[j][R+1] -= C(k + 1 — j + r — l, k + 1 — j) for all 1 <= j <= K + 1
and after that do a[i][j] = a[i][j-1] + a[i+1][j] (making a[i] as array of prefix sums array a[i+1]), a[0] will be the answer.
What is C(k + 1 — j + r — l, k + 1 — j)? This number is need for each query affect only on segment L..R, and you can see, why is it so, in Pascal's Triangle.
If this explanation is not clear for you, you can try to see other participants solutions (for example, Xellos's one).
In this task you have to find largest by area submatrix, consisting from different numbers.
Let's see solutions from slow to fast.
1) Solution by O(n6):
Iterate through two opposite vertices submatrix-answer and check that all numbers are different.
2) Solution by O(n4):
Let's fix Up and Down borders submatrix-answer (O(n2)).
Use two pointers method to iterate Left and Right borders: while in submatrix there are no equal numbers, increment Right, while there are equal numbers — increment Left. Every check — (O(n)), increments — (O(n)).
3) Solution by O(n3logn): Let's construct function maxR(Left) (let's consider that Up <= Down are fixed): maximal value Right, so that in submatrix (Up, Down, Left, Right) there is no equals numbers. You can see that maxR(i) <= maxR(i + 1) is true for every i.
How values of this function changes by shift Down to Down-1? Every value maxR(Left) can only be the same (if segment(Down, Down, Left, maxR(Left)) only added new numbers), or it can decrease.
When maxR(Left) is decreasing? Only when one of the numbers from added segment have already been in the current submatrix.
Shift Down to down let's see all numbers in row Down. For each number (let it be in column j) find indices i and k so i <= j, there is number, equal to a[Down][j] between rows Up and Down-1, i — maximal; k >= j, there is number, equal to a[Down][j] between rows Up and Down-1, k — minimal. When you find these indices (it is easy to find them using set, when you store all columns where number x was between Up and Down for all numbers x), you can try to update maxR[i] with j — 1, maxR[j] with k — 1. It will be enough, if you also update for all i = m..1 maxR[i] = min(maxR[i], maxR[i + 1]). Now maxR(Left) is correct, and you can check answer for these Up and Down by O(n).
4) Now, solution by O(n3). It requires understanding previous solution.
Previous solution, despite good asymptotics, requires to store a lot (about 160 000) sets, where you will store about 160 000 elements. Even at n = 200 it works very slow.
Let's get rid of log. Set is using only for finding nearest left and right elements, which are in rows from Up to Down, and equal to current.
Note that when you do Up = Up — 1, nearest element comes near (by column) to a[i][j], so we can find all numbers, for which the nearest element will be in new row Up, and update them nearest number, and do that in O(n2).
This solution uses O(n2) memory and O(n3) time.
BONUS: Can you solve this task faster than O(n3)? I spend a lot of time and I didn't come to any solution, but I can't show that there is not solution faster.
In this problem you have to find longest subsegment, satisfying the condition.
Reduce problem to d = 1.
If d = 0, then answer is longest subsegment from equal numbers, this case we solve separately.
If d ≠ 0, then notice that if on some subsegment there are two numbers ai, aj so that ai%d ≠ aj%d, then this segment can't be good.
Divide the sequence to consequent subsegments numbers, equal by modulo d, and divide each number by d, and solve task separately with every segment, consider that d = 1.
Notice that segment [L, R] is good if and only if when max(L, R) — min(L, R) — (R — L) <= k, and there are no equal numbers. It is easy to exlain: if there are no equal numbers, then max(L, R) — min(L, R) — (R — L) is exactly number of numbers is needed to add for segment to consist of all numbers from min(L, R) to max(L, R).
For all L lets find such maxR[L], that on segment [L..maxR[l]] there are no equal numbers, and maxR[L] is maximal. It can be done by O(nlogn) by many ways, for example you can use map.
Let's learn how we can maintain array a[R] = max(L, R) — min(L, R) — (R — L). If we have such array, then we have to find rightmost R such that a[R] <= k to get an answer.
We will need two stacks and segment tree with operations "Add number on segment", "Find min element on segment", "Find rightmost number doesn't exceed k".
Let's iterate L from right to left (n downto 1). How does function max(L, R) look like with fixed L? It's values represent a set of segments so that maximum on the segment is leftmost element of segment, and these maximums are increasing. (example: for array 6 4 8 0 7 9 function max(1, R) will be 6 6 8 8 8 9). How function changes with shift L to left? Some segments are absorbed by new element, if new element is bigger than maximum on segment. Maximums on segments are increasing, so we can keep them all in stack, and when we need to add new element we have to only pop some segments from stacks while maximum on top of stack is less then new element, and push new segment after that. If every operation with stack will be accompanied with right operation with segment tree, we can store array a[R] = max(L, R). For get array a[R] = max(L, R) — min(L, R) we need only to maintain second similar stack. For get array a[R] = max(L, R) — min(L, R) we need add -1 on all suffix when we are shitfing L.
Now query "Find fightmost number less of equal k". First, segment tree divides segment of request to log(n) segments with length powers of two. Let's choose rightmost segment with minimum <= k, and do iterative deeping there to find element that we need.
So, for every L we get query on segment L..maxR(L) on rightmost number less or equal k. It is one of candidates to an answer.
We are doing O(n) operation with stack, and every requires query to segment tree, so asymptotics is O(nlogn).











Unable to understand 407A — Triangle.
Proof for this???
I can't understand this solution too. But you may use solution with O(n^2). Like my solution,
http://codeforces.com/contest/408/submission/6183126
Fixing the point (0,0) to be the vertex of the triangle that has the right angle, you need to find 2 other points. first, we find the gcd of the given 2 distances. We try to find a point in the first quadrant such that the distance from (0,0) is the gcd. If we find one, we multiply the coordinates, to get one of the required distances. Let this point be (x,y). The slope of the line joining (0,0) and (x,y) is y/x. the slope of a line perpendicular to this line is -x/y ( -1/slope of other line). now multiply (-x,y) to get the other point. Now, we have to check if the line joining the 2 points, are parallel to the x axis/ y axis. If they are, swap the distances you used to locate the first point in the first quadrant and recalculate the second point. If they are still parallel, print NO, else print the points.
To locate a integer point, simply iterate from 1, and check if (let the distance be a) a * a — i * i is a perfect square.
Please forgive me, if its not clear. Hope it helps.
why this output incorrect ?
input 5 5
my output YES 0 0 3 4 4 3
checker log says that : wrong answer incorrect triangle
it's not a right triangle
Ok. I didn't see it must be a right triangle. Thanks.
Why can you fix that (0,0) is a vertex?
Translation doesn't change a parallelity..
The inner product of (x1,y1)、(x2,y2) is zero, which means x1*x2+y1*y2=0. Thus, x2:y2=-y1:x1.
I can't understand this solution too.
There is O(n) soln for this
my solution > 13779488
I think many people are waiting for the Tutorial of other problems!!!please!!!!!
Sorry, I am running out of time, I'll translate that part of editorial as soon as I can. If you want to see editorial right now, you can try view russian version with Google Translate.
what kind of black magic is this?!!
15ms.31ms.The time is reported witn an error of tens of miliseconds. This is well within the error margin (it's well possible that the first algorithm ran in 40 ms and the other in 0 ms).
JuanMata don't forget that there are other factors that makes O(N) requires more runtime than O(N^2) in reality , like function calls , unexpected jumps to some far locations in memory, and the data structure you use , how you manage your code , and how your code tampers the memory ...... :)
That shouldn't be it in this case. Even if the constant factor's 10 times worse, the runtime is still 100 times better on the largest inputs. What you say usually matters when comparing ,
, 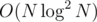 and
and 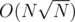 solutions, but hardly here.
solutions, but hardly here.
You could be in the same situation if you submit one source code several times.
Because there is no right triangle with such parametres.
Oh, sorry, my reply was for another comment.
I think there's a problem with this test-problem B.garland-DIV2: input : (yqfqfp/ tttwtqq) Answer is 2,right? but Checker log says: -1. Can anybody expain why?
You dont have any 't' and 'w' and you can't make 'tttwtqq' with only 'y','q' and 'f' letters
That was really a detail that you have n SHEETS and you supposed to make m PIECES completely!!
Well ......
Can someone explain the solution to problem 407C please?
I already did
How to solve the problem 407C — Curious Array. I think it is so difficult.
I already did
And I'm posting the same comment as an answer to 2 successive ones because I have bad experience with people not reading other comments before asking...
I don't care what you do! I just express my mood! Don't brainlessly deduct! ok!!!
Someone that explains 407B better)?:)
let us assume that
dp[i]be the number of moves required to start at room i and come back to i.now when we move from room i to p[i], we would have odd number of crosses on room p[i], therefore we would need
dp[p[i]]more moves to come back to p[i] and make it have even number of crosses. so afterdp[p[i]]+1moves, we would be at position p[i] + 1.solving similarly for other rooms, we can get
dp[i] = 1 + (dp[p[i]]+1) + (dp[p[i]+1]+1) + ... + (dp[i-1]+1)(the first1is the initial move from i to p[i]).now u should be able to see that the final answer would be
(dp[1]+1) + (dp[2]+1) + (dp[3]+1) + ... + (dp[n]+1).the above solution works in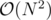 . it can be reduced to
. it can be reduced to  by using prefix sums.
by using prefix sums.
well with memo solution above still running in O(N)
same idea with me, sorry I have clicked the button of "I do not like it" by mistake ,
Thanks for the detailed explanation :)
suppose that you are in room
kthe 1st time (aka the number of crosses is odd), and the number in roomkisp[k].let
s[k]the steps you need to go from roomkto roomk+1.in order to do that:
you need
1step to go from roomkto roomp;you need
s[p[k]]+s[p[k]+1]+s[p[k]+2]+...+s[k-1]steps to go from roompto roomk. now the number of crosses is even;1step to go from roomkto roomk+1.so
s[k]=2+s[p[k]]+s[p[k]+1]+s[p[k]+2]+..+s[k-1]and of course
answer=s[1]+s[2]+..+s[n]with
n=1000solving time is30ms:)Can you explain the really short solution?
"In this problem you had to simulate route of character in graph. Note that if you are in vertice i, then edges in all vertices with numbers less than i are turned to pi. It gives us opportunity to see a recurrence formula: let dpi be number of steps, needed to get from vertice 1 to vertice i, if all edges are rotated back, into pi. Then dpi + 1 = 2dpi + 2 - dppi. Answer will be dpn + 1."
I don't really understand; what is a "rotated back" edge? What does it mean "numbers less than i are turned to pi"
Hello AkshajK, think of it this way.
dp[i+1] is composed of three sums.
dp[i+1] = S1 + S2 + S3
S1 := dp[i], since we need to get to point i first.
S2 := 2, one for the move back to p[i] and one for the jump from i to i+1
S3 is more interesting. Once, we've jumped back to p[i], how many jumps does it take to get back to i?
Jumps to reach (p[i]+1) := dp[p[i] + 1] — dp[ p[i] ] . Why? Because it's just the total number of moves to reach p[i] + 1 minus the number of jumps we needed originally to get to p[i] i.e dp[p[i]].
Thus S3 := (dp[p[i] +1] — dp[p[i]]) + (dp[p[i] +2] — dp[p[i]+1]) + ... (dp[i] — dp[i-1])
This reduces to, S3 := dp[i] — dp[p[i]]
Adding the three sums should give you the final answer.
I understood the solution. I had a simple doubt.
Let's say the input is:
2
2 2
In this case according to me, the answer should be 3 (1->2->2->3). He only used the portal three times, but according to the solution it'll give the answer as 4.
Am I missing something? Or is there an explanation?
Thanks!
what about pi<=i, here you have 2>1
6 days have passed and there are still no solutions to C-E. I can hardly call it soon...
There are no solutions for the last 3 challenging challenges, please speedup, we are waiting for that.
Why aren't there any solutions for the last 3 problems? Do the authors forget this blog???
so many statement mistakes in this tutorial!!
Anyone solving the 'Bonus' Section of Div1 B — Long Path?
I'm trying to solve 407A — Triangle, I'm not able to understand the tutorial above. Why GCD is used? Also, how did we end up taking those points?
Can someone tell me any prereq. reading that I need to do before I'll be able to understand the concepts mentioned in tutorial above?
Thanks!!
Let point where base and perpendicular meet be {x,y}. Then we can write other two points in form of the angle which line connecting them with {x,y} make with x-axes and radial distance. Let these points be {x1,y1} and {x2,y2}. Then,
x1 = x + a*cos(theta) ; y1 = y + a*sin(theta)
x2 = x — b*sin(theta) ; y2 = y + b*cos(theta)
where theta is angle between line connecting {x,y} and {x1,y1} and horizontal axes.
Now since x, x1 are integers therefore a*cos(theta) should also be integer.
Let cos(theta) = p/q. Then q should be multiple of both a and b. Smallest such q will be lcm(a,b). Now , a*cos(theta) = a*(p/lcm(a,b)) = (p/(b/g)) = (p*g)/b which can only be integer between [-a,a] since, -1 <= cos(theta) <= 1.
Other way to optimize D:
Instead of using set use bitset of size maxn initially filled with zeros. Anytime we insert value at point i just set ith bit to 1. To find next filled element we can just use _Find_next on bitset, sadly bitset has no _Find_prev, but we can use #define private public to bypass it and implement our own _Find_prev
Code: 55948192