The-Winner's blog

Minimum/maximum distance between coprime nodes
By The-Winner, 11 months ago, In English

I was wondering if there is any faster algorithm than O(N^2) that solves the following problem: Given a tree made of N nodes, where each node has an integer value asociated to it, find the minimum/maximum distance between two nodes whose values are coprime(if such a pair exists).

For example, given the following tree:

The minimum distance is 1 and can be obtained in multiple ways, but one of them is:

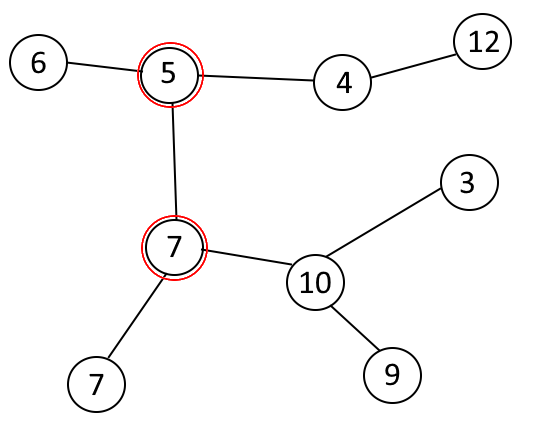
And the maximum distance is 4 and can be obtained like this:

I couldn't find anything like this by googling so I thought this is the best place to ask. Thank you in advance.

  • Vote: I like it
  • +41
  • Vote: I do not like it

»
11 months ago, # |
  Vote: I like it -9 Vote: I do not like it

What's the constraint for ai

→ Reply
  • »
    »
    11 months ago, # ^ |
      Vote: I like it -7 Vote: I do not like it

    I didn't find this problem anywhere, just thought about it, I suppose you can make it <=N or <=1e6 or 1e7.

    → Reply
»
11 months ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Deleted.

→ Reply
»
11 months ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

It can be solved using centroid decomposition but I'm not aware of the details

→ Reply
»
11 months ago, # |
  Vote: I like it +21 Vote: I do not like it

By using centroid decomposition you can turn the problem into finding $$$b_i = \max_{i\perp j} a_j$$$, which can be solved by using parallel binary search in $$$O(n \log n 2^{\omega(n)})$$$.The whole complexity is $$$O(n \log^2 n 2^{\omega(n)})$$$.

→ Reply
  • »
    »
    11 months ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    How are you using parallel binary search if there are no queries ?

    → Reply
    • »
      »
      »
      11 months ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Each $$$b_i$$$ is a query.

      → Reply