Consider the following problem :
Your are given an array $$$a$$$ of size $$$n$$$ and $$$q$$$ queries of form $$$(l_1, r_1), (l_2, r_2), ..., (l_q, r_q)$$$. For each query you have to find the MEX of the array $$$a_l, a_{l+1}, ..., a_r$$$. The queries are offline.
$$$0 \le a_1, a_2, ..., a_n \le n$$$
$$$1 \le l_i \le r_i \le n$$$, for all $$$1 \le i \le q$$$
The approach to the problem is discussed in the comment here.
First let's consider a special case of the queries where $$$r = n$$$. In this case we want to find the smallest integer that does not occur in the subarray $$$a_l, ..., a_r$$$. That is, the smallest integer that does not occur at index $$$l$$$ or after it.
For all $$$0 \le x \le n$$$, let $$$b_x$$$ be the greatest index $$$i$$$ such that $$$a_i = x$$$, and $$$0$$$ if no such $$$a_i$$$ exists.
Now the MEX say $$$m$$$ of subarray $$$a_l, ..., a_n$$$ either does not occur in $$$a$$$, in which case we have $$$b_m = 0$$$, or the last occurence of $$$m$$$ in $$$a$$$ is before $$$l$$$, thus $$$b_m < l$$$. We can say that $$$m$$$ is the minimum of all such numbers, thus $$$m$$$ = $$$min$$$ { $$$i$$$ | $$$b_i < l$$$ }.
Now since the queries are offline, we can sort the queries by $$$r$$$ and process them such that we can ignore the subarray $$$a_{r + 1}, ..., a_n$$$. We iterate from from $$$r = 1, 2, ..., n$$$, and for each $$$r$$$ we process all queries $$$(l_i, r_i)$$$ where $$$r_i = r$$$.
Now how do we efficiently calculate the answer for queries $$$(l, n)$$$ ?
We maintain a minimum segment tree on the array $$$b$$$ and update all values for $$$i = 1, 2, ..., r$$$. Now since there are $$$n$$$ updates but $$$n + 1$$$ leaf nodes in the segment tree, at least one of them is zero. So value of root node is $$$0$$$. Now we try to find the minimum index leaf node with value < $$$l$$$. We start at root node and travel down to this node. At each node we see if the value of it's left child is < $$$l$$$. If it is we go to left child. Otherwise we go to the right child. Either of left or right child will always have value < $$$l$$$. Finally we reach a leaf node, the index of this node(after adjusting for offset) is the mex of array $$$a_l, a_{l + 1}, ..., a_r$$$.
Consider the array $$$a = [6, 1, 0]$$$.
Here $$$b = [3, 2, 0, 0, 0, 0, 1, 0]$$$.
Consider evaluation for $$$l = 2, r = 3$$$. The subarray is $$$[a_2, a_3] = [1, 0]$$$.
We start at root node.
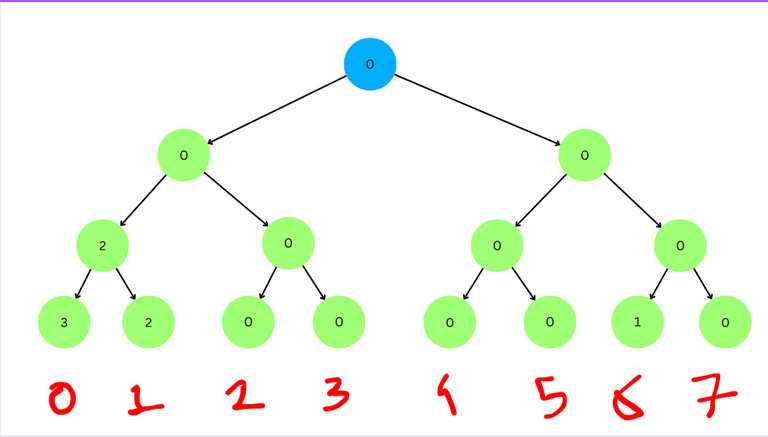
We see that the left child has value < $$$l$$$, so we go to the left child.
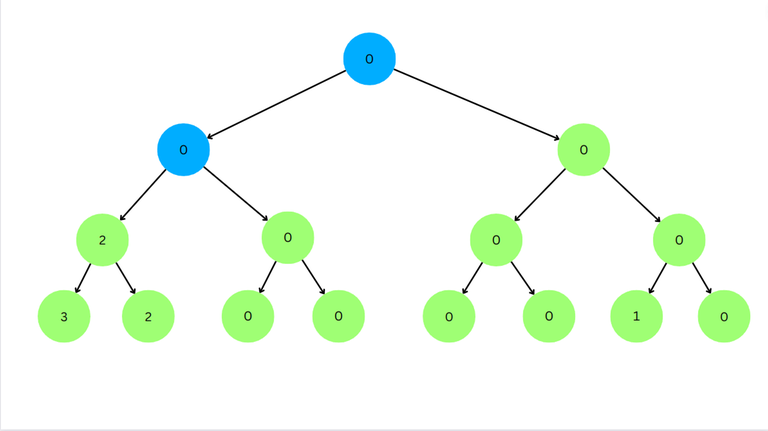
Now for left node $$$2 \ge l$$$. So we go to right node.
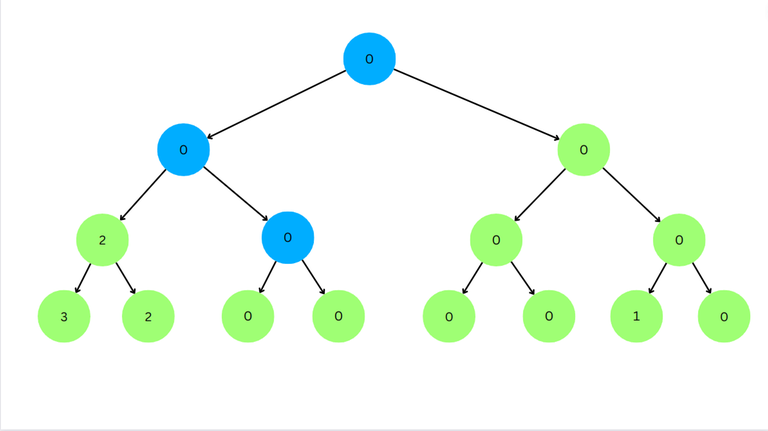
Now for the left child value < $$$l$$$. So we go to left child.
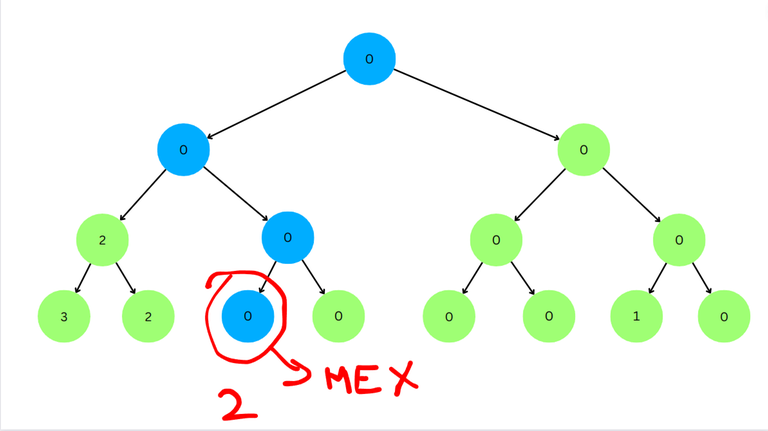
We have reached a leaf node. The corresponding index is 2 and thus the MEX of the subarray $$$[a_2, a_3]$$$ is 2.
Calculating MEX of each query takes $$$O(log n)$$$ time, total $$$O(q log n)$$$. Updating the tree for $$$b$$$ takes $$$O(n log n)$$$ time in total. Sorting $$$q$$$ queries takes $$$O(q log q)$$$ time.
Overall time complexity — $$$O(n log n + q(log n + log q))$$$
#include<bits/stdc++.h>
using namespace std;
#define ll long long
struct SegmentTree{
int n;
vector<int> tree;
SegmentTree(int sz){
n = 1;
while(n < sz){
n <<= 1;
}
tree.assign(2 * n, 0);
}
void set(int ind, int val){
ind += n;
tree[ind] = val;
ind >>= 1;
while(ind > 0){
tree[ind] = min(tree[2 * ind], tree[2 * ind + 1]);
ind >>= 1;
}
}
int get(int x){
// return the first index i, such that s[i] < x
int node = 1;
while(node < n){
int left = (node << 1);
int right = (node << 1) + 1;
if(tree[left] < x){
node = left;
}else{
node = right;
}
}
return (node - n);
}
};
int main(){
int n;
cin >> n;
vector<int> a(n + 1);
for(int i = 1; i <= n; ++i){
cin >> a[i];
}
int q;
cin >> q;
vector<vector<pair<int, int>>> queries(n + 1);
for(int i = 0; i < q; ++i){
int l, r;
cin >> l >> r;
queries[r].push_back({l, i});
}
vector<int> res(q);
SegmentTree s(n + 1);
for(int i = 1; i <= n; ++i){
// set the last occurence of a[i] to i
s.set(a[i], i);
for(auto [l, ind] : queries[i]){
// find the smallest x, such that last occurence of x < l
res[ind] = s.get(l);
}
}
for(int elem : res){
cout << elem << '\n';
}
cout << '\n';
return 0;
}











Auto comment: topic has been updated by one_autum_leaf (previous revision, new revision, compare).
Practice question
https://leetcode.com/problems/smallest-missing-genetic-value-in-each-subtree/description/
Problem
Find the sum of answers to queries of Type2. Since the answer can be large, return it modulo 1e9 + 7.
Constants:
1 <= N <= 10 ^ 5,
1 <= A[i] <= 10 ^ 5,
1 <= P[i] <= 10 ^ 5,
1 <= Q <= 10 ^ 5,
3 <= Col <= 3, 1 <=T[I][j] <=10 ^ 5
I am thinking of making dfs tree array and work on this array. But how do we solve range MEX queries with update on array?
Did you think of square root decomposition?
How will you combine results from two square roots? We can't work with frequency for each square root.
Can be done easily in $$$\mathcal{O}(n^{5/3}+q\sqrt{n})$$$ via 3D Mo and a bit harder in $$$\mathcal{O}(n \log{n}+q\log^2{n})$$$. For the second approach, if the value of $$$x$$$ is at positions $$$p_1, p_2 \dots p_k$$$, consider segments $$$[1; p_1 - 1]$$$, $$$[p_1+1, p_2-1]$$$ ... $$$[p_{k-1}+1;p_k - 1]$$$, $$$[p_k+1, n]$$$ with the value of $$$x$$$ associated with these segments. There will be a total of $$$\mathcal{O}(n)$$$ such segments, and each update changes only $$$\mathcal{O}(1)$$$ of them. And for a range MEX query, we need to find the segment with the smallest $$$x$$$ for all the segments in which the query segment is nested. This can be done for $$$\mathcal{O}(\log^2{n})$$$ in various ways using data structures.
practice https://codeforces.com/gym/105242/problem/A