Hi everyone again! Recently, solving the problem 1937 from Timus (by the way, I recommend it to you too! It is a great opportunity to improve yourself in string algorithms), I was faced with the necessity of finding all subpalindromes in the string. Experienced programmers already know that one of the best algorithms for this is Manacher's algo that allows you to get all subpalindromes in compressed form without any additional structures. The only problem — the algorithm is kinda hard to implement. That is, its idea is simple and straightforward, but the implementation usually are heaps of code to the widespread consideration of where to write +1, and where -1.
For those who do not know or do not remember, I will describe briefly the Manacher's algorithm. Conciseness in memory is achieved through the fact that we do not store the indices of palindromes, and for each item in the string we store the half of the length of the largest palindrome, for which item is central. If we are talking about palindromes of even length, we consider the central element to the right of exact center.
Further, we keep the left and the right ends of the rightmost palindrome and, just as it done in the Z-function, we firstly try to initialize the value of the array at this point, using information that is already computed, and then we continue with naive algorithm. To be precise, we can initialize the value of p[i] from the point that is symmetric to it in the rightmost palindrome, i.e. from p[l + (r - i)]. If we talk about palindromes of even length (you already hate them just like me, right?), Then we are interested in the value of p[l + (r - i) + 1]. And yes, it is necessary not to forget that after initialization we should not have to go beyond the known part of the string, i.e. it is necessary to initialize with something that is not more than r - i ( or r - i + 1 for palindromes of even length).
That's how e-maxx offers to use Manacher's algo:
vector<int> d1 (n);
int l=0, r=-1;
for (int i=0; i<n; ++i) {
int k = (i>r ? 0 : min (d1[l+r-i], r-i)) + 1;
while (i+k < n && i-k >= 0 && s[i+k] == s[i-k]) ++k;
d1[i] = k--;
if (i+k > r)
l = i-k, r = i+k;
}
vector<int> d2 (n);
l=0, r=-1;
for (int i=0; i<n; ++i) {
int k = (i>r ? 0 : min (d2[l+r-i+1], r-i+1)) + 1;
while (i+k-1 < n && i-k >= 0 && s[i+k-1] == s[i-k]) ++k;
d2[i] = --k;
if (i+k-1 > r)
l = i-k, r = i+k-1;
}
Two almost similar pieces of code for palindromes of even and odd length. And, if my memory serves me, and it's still not fixed, they also contain an error (can you find it?)
A little thought and writing out some cases on a piece of paper, I was able to squeeze two separate pieces into one. At the same time, I tried to keep the maximum similarity with the Z-function algorithm.
vector<vector<int>> p(2,vector<int>(n,0));
for(int z=0,l=0,r=0;z<2;z++,l=0,r=0)
for(int i=0;i<n;i++)
{
if(i<r) p[z][i]=min(r-i+!z,p[z][l+r-i+!z]);
while(i-p[z][i]-1>=0 && i+p[z][i]+1-!z<n && s[i-p[z][i]-1]==s[i+p[z][i]+1-!z]) p[z][i]++;
if(i+p[z][i]-!z>r) l=i-p[z][i],r=i+p[z][i]-!z;
}
}
However, long enough string with while spoils the whole picture. I propose to fight with it like this:
vector<vector<int>> p(2,vector<int>(n,0));
for(int z=0,l=0,r=0;z<2;z++,l=0,r=0)
for(int i=0;i<n;i++)
{
if(i<r) p[z][i]=min(r-i+!z,p[z][l+r-i+!z]);
int L=i-p[z][i], R=i+p[z][i]-!z;
while(L-1>=0 && R+1<n && s[L-1]==s[R+1]) p[z][i]++,L--,R++;
if(R>r) l=L,r=R;
}
As it seems to me, this is the most readable version of the code. And what do you think about this? How to implement Manacher's algo least painful? And in general, how do you solve the problem of finding all subpalindromes in the string? Share your ideas in the comments below :)
P.S. It looks like my English is especially poor in this entry. My apologies about it :(
UPD: droptable said in the comments on how to support arrays from Manacher's algorithm in online. Here I put an example of the algorithm itself, with some modifications, which will be discussed below.
The basic idea of the algorithm: at any time we keep the center of the longest palindrome relating to the right end of the line. When we add character to the end, we have two options for what happens next:
- Main palindrome expands. Then we simply increase its radius value and return.
- Main palindrome not expands. This means that we will need to traverse an array forward to find new primary palindrome. Thus, each time a new cell initializing with number in the cell that is symmetrical to the center of the previous main palindrome. Once it turned out that we can extend the current palindrome, which means that it is leftmost of the related to the end of the string and then it will become the new main palindrome.
Now about the changes in the code. First, were deleted the two empty characters that were inserted into the string at the begin. As it turned out, they are not necessary, however, but their addition to their complexity algorithm.
Second, was added get(). Mikhail mentioned in his comment about some problems with online. The problem was that, in any moment, we know only the final values in the elements, which are earlier than the center of the main palindrome. However, you will notice that the values after it, we can get in O(1) if we will refer to symmetric from the center of the main palindrome element.











I think this may be helpful : http://leetcode.com/2011/11/longest-palindromic-substring-part-ii.html
I solved that problem in O(N*logN) using Hash. I think Hashing can replace Manacher entirely, can apply to more types of problem and is easier to implement :)
by hashing? how nlogn can u explain your process?
We choose position x and then find with bin_search the maximal palindrome with the middle in x!And we can compare two strings with the hashes in o(1)!
Can you please share your code? The problem which i am facing is while during binary search, even if the hash value is same on both the sides of the current x, it does not mean that the substrings will be the same, as there can be collisions. How do we handle this scenario?
Edit: However, i used double hashing to assume there will be no false positives, however this is still not accurate. Any leads would be definitely helpful.
If you feel insecure about a single hash just use two and you'll pretty much never run into any problems.
hey you sucker .... you published this before 2 days and APIO contest was running ... this algorithm is very useful for the first task
If i've read this during APIO I would've scored 100 points on the first task
and guess what it was published DURING THE CONTEST
Did the competitors have an Internet access during the APIO?
yes .... it's held online and the contest was runned for 2 days each delegation has an assigned time to do it
It's an unpleasant coincidence. I didn't know about APIO problems. Anyway, Manacher is pretty well-known algo and if you diligently searched for it, I guarantee that you would find something else even if my entry was not published. Also, you could made arrays from Manacher's algo with straightforward algorithm with hashing in O(nlogn). Anyway, my apologies, but I don't think that my entry seriously harmed APIO.
Actually I said that because you published them in the first day of APIO (manacher + suffix trees) and anyone of them is a key to solve the first problem ... BTW thanks for the blogs i believe they are too helpful i will read them soon
I published entry about suffix tree much earlier...
Here is the link to my implementation, it's a bit different to your code. Also it includes a function (quiet trivial) that is useful for checking if a given substring s[b...e] is palindrome.
Can you please explain how you solved the Timus problem 1937 using Manacher's algorithm?
How common are Manachers' algo problems on Codeforces? Could someone give me links to some questions here on Codeforces.
Huh, readability is incredible in this article :)
Here is actual version:
Could you please explain what this code does in more detailed?
If this code is about Manacher's algorithm then I think it is wrong.
It calculates half-length of maximum odd palindrome with center in . For example, for
. For example, for 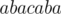 it returns
it returns  .
.
What is the use of characters "@" and "$"?
Using them we can get rid of cases when i - len or i + len are out of bound.
Can you please also put readable code for even palindromes?
In case of even palindromes I suggest to use the same code with the string s1#s2#... #sn
I made a mistake.
For input: "ArozaupalanalapuazorA"
Gives output: "1 1 1 1 1 1 1 1 2 1 11 1 2 1 1 1 1 1 1 1 1".
So, it works fine.
We can also solve this problem using Dynamic Programming using O(N^2) time and memory. We will store array dp[i][j] to memoize the function: f(i,j) = 1 if substring [i..j] is palindrome and 0 otherwise.
The base cases are all f(i,i) because a length 1 substring is always a palindrome, and also f(i,i+1) is a base case, because if s[i] = s[i+1] then f(i,i+1) = 1, otherwise f(i,i+1) = 0.
When i < j-1, f(i,j) = 1 iff f(i+1,j-1) = 1 and s[i] = s[j], otherwise f(i,j) = 0. So we can run f(i,j) for every pair (i,j) and in the end we will have a boolean matrix that will contain the indices (i,j) of every palindromic substring.
This algorithm should be optimal because we can have O(N^2) palindromic substrings (when every character is equal), so any algorithm that retrieves all of them should be at least O(N^2).
Here is my version:
It returns the array
L[i]— index of the beginning of the longest palindrome centered at positioni. (For both even and odd positions simultaneously.) If you need the end index, it is calculated by symmetry:R[i] = i - L[i]. And of course, the length of the palindrome islen[i] = R[i]-L[i]+1 = i - 2*L[i] + 1.I found much shorter implementation https://github.com/stjepang/snippets/blob/master/manacher.cpp
I like this implementation:
Is above piece of code works for both odd and even length palindromes or we have to do something more for even length palindromes ??