Information about the round
| Person | A | B | C | D | E | F1 | F2 |
|---|---|---|---|---|---|---|---|
| sum | 800 | 1300 | 1500 | 1900 | 2000 | 2200 | 2900 |
| oursaco | 800 | 1100 | 1300 | 1600 | 1800 | 2100 | 3100 |
| omeganot | 900 | 1000 | 1400 | 1700 | 1900 | 2200 | 2800 |
| SriniV | 1900 | 2000 | 1900 | ||||
| Apple_Method | 1000 | 1200 | 1400 | 1900 | 1600 | ||
| awesomeguy856 | 800 | 1100 | 1400 | 1800 | 1900 | 2000 | 2800 |
| nonrice | 900 | 1000 | 1400 | 1750 | |||
| null_awe | 800 | 1100 | 1300 | 1700 | 1900 | 2000 | 2600 |
| htetgm | 900 | 1000 | 1200 | 1700 | 2000 | ||
| thehunterjames | 900 | 1300 | 1600 | 1900 | |||
| Yam | 800 | 1100 | 1500 | 1800 | 2000 | 2100 | |
| GusterGoose27 | 3000 |
| A | B | C | D | E | F1 | F2 | |
|---|---|---|---|---|---|---|---|
| Average | 860 | 1120 | 1400 | 1786 | 1900 | 2071 | 2867 |
| Actual | 800 | 1100 | 1500 | 1800 | 2100 | 2500 | 3000 |
We would like to thank Artyom123 for feedback on every problem and immense help with problem preparation. We would also like to thank all the testers for their valuable feedback which greatly improved the round. The editorial was prepared by sum and omeganot.
| Problem | Preparation | |
|---|---|---|
| A | sum | sum |
| B | sum | sum |
| C | omeganot | omeganot |
| D | sum | sum, omeganot |
| E | sum | sum |
| F1 & F2 | sum | sum, omeganot |
Solutions
1920A - Satisfying Constraints
Suppose there are no $$$\neq$$$ constraints. How would you solve the problem? How would you then factor in the $$$\neq$$$ constraints into your solution?
Let's first only consider the $$$\geq$$$ and $$$\leq$$$ constraints. The integers satisfying those two constraints will be some contiguous interval $$$[l, r]$$$. To find $$$[l,r]$$$, for each $$$\geq x$$$ constraint, we do $$$l := \max{(l, x)}$$$ and for each $$$\leq x$$$ constraint, we do $$$r := \min{(r, x)}$$$.
Now, for each, $$$\neq x$$$ constraint, we check if $$$x$$$ is in $$$[l, r]$$$. If so, we subtract one from the answer (remember that there are no duplicate constraints). Let the total number of times we subtract be $$$s$$$. Then our answer is $$$\max{(r-l+1-s,0)}$$$. The time complexity of this solution is $$$O(n)$$$.
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n;
cin >> n;
int l = 1;
int r = 1e9;
int s = 0;
vector<int> neq;
for (int i = 0; i < n; i++){
int a, x;
cin >> a >> x;
if (a == 1)
l = max(l, x);
if (a == 2)
r = min(r, x);
if (a == 3)
neq.push_back(x);
}
for (int x : neq)
if (x >= l and x <= r)
s++;
cout<<max(r - l + 1 - s, 0)<<"\n";
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
int tc;
cin >> tc;
while (tc--)
solve();
}
1920B - Summation Game
What is the optimal strategy for Bob?
It is optimal for Bob to negate the $$$x$$$ largest elements of the array. So what should Alice do?
It is optimal for Bob to negate the $$$x$$$ largest elements of the array. So in order to minimize the damage Bob will do, Alice should always remove some number of largest elements.
To solve the problem, we can sort the array and iterate over $$$i$$$ ($$$0 \leq i \leq k$$$) where $$$i$$$ is the number of elements Alice removes. For each $$$i$$$, we know that Alice will remove the $$$i$$$ largest elements of the array and Bob will then negate the $$$x$$$ largest remaining elements. So the sum at the end can be calculated quickly with prefix sums. The time complexity is $$$O(n \log n)$$$ because of sorting.
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n, k, x;
cin >> n >> k >> x;
int A[n + 1] = {};
for (int i = 1; i <= n; i++)
cin >> A[i];
sort(A + 1, A + n + 1, greater<int>());
for (int i = 1; i <= n; i++)
A[i] += A[i - 1];
int ans = -1e9;
for (int i = 0; i <= k; i++)
ans = max(ans, A[n] - 2 * A[min(i + x, n)] + A[i]);
cout<<ans<<"\n";
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
int tc;
cin >> tc;
while (tc--)
solve();
}
1920C - Partitioning the Array
Try to solve the problem for just two integers $$$x$$$ and $$$y$$$. Under what $$$m$$$ are they equal (modulo $$$m$$$)?
How can we use the previous hint and gcd to solve the problem?
For some $$$x$$$ and $$$y$$$, let's try to find all $$$m$$$ such that $$$x \bmod m \equiv y \bmod m$$$. We can rearrange the equation into $$$(x-y) \equiv 0 \pmod m$$$. Thus, if $$$m$$$ is a factor of $$$|x-y|$$$, then $$$x$$$ and $$$y$$$ will be equal modulo $$$m$$$.
Let's solve for some $$$k$$$. A valid partition exists if there exists some $$$m>1$$$ such that the following is true:
- $$$a_1 \equiv a_{1+k} \pmod m$$$
- $$$a_2 \equiv a_{2+k} \pmod m$$$
- ...
- $$$a_{n-k} \equiv a_{n} \pmod m$$$
The first condition $$$a_1 \equiv a_{1+k} \pmod m$$$ is satisfied if $$$m$$$ is a factor of $$$|a_1-a_{1+k}|$$$. The second condition $$$a_2 \equiv a_{2+k} \pmod m$$$ is satisfied if $$$m$$$ is a factor of $$$|a_2-a_{2+k}|$$$. And so on...
Thus, all conditions are satisfied if $$$m$$$ is a factor of:
In other words, all conditions are satisfied if $$$m$$$ is a factor of:
So a valid $$$m$$$ exists for some $$$k$$$ if the aforementioned $$$\gcd$$$ is greater than $$$1$$$.
We can iterate over all possible $$$k$$$ (remember that $$$k$$$ is a divisor of $$$n$$$) and solve for each $$$k$$$ to get our answer. The time complexity of this will be $$$O((n + \log n) \cdot \text{max divisors of n})$$$. Note that each pass through the array takes $$$n + \log n$$$ time because of how the gcd will either be halved or stay the same at each point.
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n;
cin >> n;
int A[n];
for (int &i : A)
cin >> i;
int ans = 0;
for (int k = 1; k <= n; k++){
if (n % k == 0){
int g = 0;
for (int i = 0; i + k < n; i++)
g = __gcd(g, abs(A[i + k] - A[i]));
ans += (g != 1);
}
}
cout<<ans<<"\n";
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
int tc;
cin >> tc;
while (tc--)
solve();
}
1920D - Array Repetition
For some query try to trace your way back to where the $$$k$$$-th number was added.
Here's an example of tracing back:
Suppose the $$$k$$$-th element is the bolded $$$l_2$$$. Finding the $$$k$$$-th element is equivalent to finding the ($$$k \bmod x$$$)-th element (unless if $$$k \bmod x$$$ is $$$0$$$).
First, let's precalculate some things:
Now, let's try answering some query $$$k$$$. If we have some $$$dp_i=k$$$ then the answer is $$$lst_i$$$.
Otherwise, let's find the first $$$i$$$ such that $$$dp_i > k$$$. This $$$i$$$ will be a repeat operation and our answer will lie within one of the repetitions. Our list at this point will look like:
Let the $$$k$$$-th element be the bolded $$$l_2$$$ of the final repetition. As you can see, finding the $$$k$$$-the element is equivalent to finding the $$$(k \bmod dp_{i-1})$$$-th element. Thus, we should do $$$k:=k \bmod dp_{i-1}$$$ and repeat! But there is one more case! If $$$k \equiv 0 \pmod {dp_{i-1}}$$$ then the answer is $$$lst_{i-1}$$$.
At this point there are 2 ways we can go about solving this:
Notice that after $$$\log{(\max{k})}$$$ operations of the second type, the number of elements will exceed $$$\max{k}$$$. So we only care about the first $$$\log{(\max{k})}$$$ operations of the second type. Thus, iterate through the $$$\log{(\max{k})}$$$ operations of the second type backwards and perform the casework described above. This leads to a $$$O(n+q\log{(\max{k})})$$$ solution or a $$$O(n+q(\log{(\max{k})}+\log n))$$$ solution depending on implementation details.
Observe that $$$k:=k \bmod dp_{i-1}$$$ will reduce $$$k$$$ by at least half. If we repeatedly binary search for the first $$$i$$$ such that $$$dp_i \geq k$$$, and then do $$$k:=k \bmod dp_{i-1}$$$ (or stop if it's one of the other cases), then each query will take $$$O(\log n\log k)$$$ time so the total time complexity will be $$$O(n+q\log n\log {(\max{k})})$$$.
#include <bits/stdc++.h>
using namespace std;
#define ll long long
void solve(){
int n, q;
cin >> n >> q;
ll dp[n + 1] = {};
int lstAdd[n + 1] = {};
vector<int> pos;
for (int i = 1, doAdd = true; i <= n; i++){
int a, v;
cin >> a >> v;
if (a == 1){
lstAdd[i] = v;
dp[i] = dp[i - 1] + 1;
}
else{
lstAdd[i] = lstAdd[i - 1];
dp[i] = ((v + 1) > 2e18 / dp[i - 1]) ? (ll)2e18 : dp[i - 1] * (v + 1);
if (doAdd)
pos.push_back(i);
}
// No need to consider any more repetitions after this point
if (dp[i] == 2e18)
doAdd = false;
}
while (q--){
ll k;
cin >> k;
for (int i = pos.size() - 1; ~i; i--){
int idx = pos[i];
if (dp[idx] > k and dp[idx - 1] < k){
if (k % dp[idx - 1] == 0){
k = dp[idx - 1];
break;
}
k %= dp[idx - 1];
}
}
cout<<lstAdd[lower_bound(dp + 1, dp + n + 1, k) - dp]<<" \n"[q == 0];
}
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
int tc;
cin >> tc;
while (tc--)
solve();
}
#include <bits/stdc++.h>
using namespace std;
#define ll long long
void solve(){
int n, q;
cin >> n >> q;
ll dp[n + 1] = {};
int lstAdd[n + 1] = {};
for (int i = 1; i <= n; i++){
int a, v;
cin >> a >> v;
if (a == 1){
lstAdd[i] = v;
dp[i] = dp[i - 1] + 1;
}
else{
lstAdd[i] = lstAdd[i - 1];
dp[i] = ((v + 1) > 2e18 / dp[i - 1]) ? (ll)2e18 : dp[i - 1] * (v + 1);
}
}
while (q--){
ll k;
cin >> k;
while (true){
int pos = lower_bound(dp + 1, dp + n + 1, k) - dp;
if (dp[pos] == k){
cout<<lstAdd[pos]<<" \n"[q == 0];
break;
}
if (k % dp[pos - 1] == 0){
cout<<lstAdd[pos - 1]<<" \n"[q == 0];
break;
}
k %= dp[pos - 1];
}
}
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
int tc;
cin >> tc;
while (tc--)
solve();
}
1920E - Counting Binary Strings
How do you count the number of good substrings in a string?
We can count the number of good substrings in a string with the counting contribution technique. Now try to solve this problem with dynamic programming.
$$$\frac{n}{1} + \frac{n}{2} + \cdots + \frac{n}{n} = O(n\log n)$$$
Let's first solve the problem where we are given some string $$$s$$$ and must count the number of good substrings. To do this we use the technique of counting contributions. For every $$$1$$$ in $$$s$$$, we find the number of good substrings containing that $$$1$$$. Consider the following example:
The number of good substrings in this example is $$$a_1 a_2 + a_2 a_3 + a_3 a_4 + a_4 a_5$$$. We can create such array for any string $$$s$$$ and the number of good substrings of $$$s$$$ is the sum of the products of adjacent elements of the array.
This motivates us to reformulate the problem. Instead, we count the number of arrays $$$a_1,a_2,...,a_m$$$ such that every element is positive and the sum of the products of adjacent elements is exactly equal to $$$n$$$. Furthermore, every pair of adjacent elements should have sum minus $$$1$$$ be less than or equal to $$$k$$$. We can solve this with dynamic programming.
The key observation is that we only have to iterate $$$p$$$ up to $$$\lfloor \frac{i}{j} \rfloor$$$ (since if $$$p$$$ is any greater, $$$j \cdot p$$$ will exceed $$$i$$$). At $$$j=1$$$, we will iterate over at most $$$\lfloor \frac{i}{1} \rfloor$$$ values of $$$p$$$. At $$$j=2$$$, we will iterate over at most $$$\lfloor \frac{i}{2} \rfloor$$$ values of $$$p$$$. In total, at each $$$i$$$, we will iterate over at most $$$\lfloor \frac{i}{1} \rfloor + \lfloor \frac{i}{2} \rfloor +\cdots + \lfloor \frac{i}{i} \rfloor \approx i \log i$$$ values of $$$p$$$. Thus, the time complexity of our solution is $$$O(nk\log n)$$$.
#include <bits/stdc++.h>
using namespace std;
const int md = 998244353;
void solve(){
int n, k;
cin >> n >> k;
int dp[n + 1][k + 1] = {};
int ans = 0;
fill(dp[0] + 1, dp[0] + k + 1, 1);
for (int sum = 1; sum <= n; sum++){
for (int cur = 1; cur <= k; cur++){
for (int prv = 1; cur * prv <= sum and cur + prv - 1 <= k; prv++)
dp[sum][cur] = (dp[sum][cur] + dp[sum - cur * prv][prv]) % md;
if (sum == n)
ans = (ans + dp[sum][cur]) % md;
}
}
cout<<ans<<"\n";
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
int tc;
cin >> tc;
while (tc--)
solve();
}
1920F1 - Smooth Sailing (Easy Version)
Use the fact that a good some path $$$p$$$ fully encircles the island if it is impossible to go from an island cell to a cell on the border by only travelling to adjacent or diagonal cells without touching a cell on path $$$p$$$.
Binary search!
For each non-island cell $$$(i, j)$$$, let $$$d_{i,j}$$$ be the minimum Manhattan distance of cell $$$(i, j)$$$ to an underwater volcano. We can find all $$$d_{i,j}$$$ with a multisource BFS from all underwater volcanos. The danger of a round trip is the smallest value of $$$d_{u,v}$$$ over all $$$(u, v)$$$ in the path.
For each query, binary search on the answer $$$k$$$ — we can only visit cell ($$$i, j$$$) if $$$d_{i,j} \geq k$$$. Now, let's mark all cells ($$$i, j$$$) ($$$d_{i,j} \geq k$$$) reachable from ($$$x, y$$$). There exists a valid round trip if it is not possible to go from an island cell to a border cell without touching a marked cell.
The time complexity of this solution is $$$O(nm \log{(n+m)})$$$.
#include <bits/stdc++.h>
using namespace std;
const int mx = 3e5 + 5;
const int diAdj[4] = {-1, 0, 1, 0}, djAdj[4] = {0, -1, 0, 1};
const int diDiag[8] = {0, 0, -1, 1, -1, -1, 1, 1}, djDiag[8] = {-1, 1, 0, 0, -1, 1, 1, -1};
int n, m, q, islandi, islandj; string A[mx]; vector<int> dist[mx]; vector<bool> reachable[mx], islandVis[mx]; queue<pair<int, int>> bfsQ;
bool inGrid(int i, int j){
return i >= 0 and i < n and j >= 0 and j < m;
}
bool onBorder(int i, int j){
return i == 0 or i == n - 1 or j == 0 or j == m - 1;
}
void getReach(int i, int j, int minVal){
if (!inGrid(i, j) or reachable[i][j] or dist[i][j] < minVal or A[i][j] == '#')
return;
reachable[i][j] = true;
for (int dir = 0; dir < 4; dir++)
getReach(i + diAdj[dir], j + djAdj[dir], minVal);
}
bool reachBorder(int i, int j){
if (!inGrid(i, j) or reachable[i][j] or islandVis[i][j])
return false;
if (onBorder(i, j))
return true;
islandVis[i][j] = true;
bool ok = false;
for (int dir = 0; dir < 8; dir++)
ok |= reachBorder(i + diDiag[dir], j + djDiag[dir]);
return ok;
}
bool existsRoundTrip(int x, int y, int minVal){
// Reset
for (int i = 0; i < n; i++){
reachable[i] = vector<bool>(m, false);
islandVis[i] = vector<bool>(m, false);
}
// Get all valid cells you can reach from (x, y)
getReach(x, y, minVal);
// Check if the valid cells you can reach from (x, y) blocks the island from the border
return !reachBorder(islandi, islandj);
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
cin >> n >> m >> q;
for (int i = 0; i < n; i++){
cin >> A[i];
dist[i] = vector<int>(m, 1e9);
for (int j = 0; j < m; j++){
if (A[i][j] == 'v'){
dist[i][j] = 0;
bfsQ.push({i, j});
}
if (A[i][j] == '#'){
islandi = i;
islandj = j;
}
}
}
// Multisource BFS to find min distance to volcano
while (bfsQ.size()){
auto [i, j] = bfsQ.front(); bfsQ.pop();
for (int dir = 0; dir < 4; dir++){
int ni = i + diAdj[dir], nj = j + djAdj[dir];
if (inGrid(ni, nj) and dist[i][j] + 1 < dist[ni][nj]){
dist[ni][nj] = dist[i][j] + 1;
bfsQ.push({ni, nj});
}
}
}
while (q--){
int x, y;
cin >> x >> y;
x--; y--;
int L = 0, H = n + m;
while (L < H){
int M = (L + H + 1) / 2;
existsRoundTrip(x, y, M) ? L = M : H = M - 1;
}
cout<<L<<"\n";
}
}
1920F2 - Smooth Sailing (Hard Version)
How do we check if a point is inside a polygon using a ray?
If u draw line from island cell extending all the way right, an optimal round trip will cross this line an odd number of times.
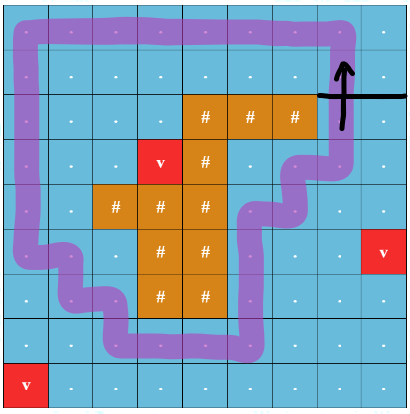
What can your state be? How can we simplify this problem down into finding the path that maximizes the minimum node? How can we solve this classic problem?
For each non-island cell $$$(i, j)$$$, let $$$d_{i,j}$$$ be the minimum Manhattan distance of cell $$$(i, j)$$$ to an underwater volcano. We can find all $$$d_{i,j}$$$ with a multisource BFS from all underwater volcanos. The danger of a round trip is the smallest value of $$$d_{u,v}$$$ over all $$$(u, v)$$$ in the path.
Consider any island cell. We can take inspiration from how we check whether a point is in a polygon — if a point is inside the polygon then a ray starting from the point and going in any direction will intersect the polygon an odd number of times. Draw an imaginary line along the top border of the cell and extend it all the way to the right of the grid.

We can observe that an optimal round trip will always cross the line an odd number of times.
Using this observation, we can let our state be $$$(\text{row}, \, \text{column}, \, \text{parity of the number of times we crossed the line})$$$. Naively, we can binary search for our answer and BFS to check if $$$(x, y, 0)$$$ and $$$(x, y, 1)$$$ are connected. This solves the easy version of the problem.
To fully solve this problem, we can add states (and their corresponding edges to already added states) one at a time from highest $$$d$$$ to lowest $$$d$$$. For each query $$$(x, y)$$$, we want to find the first time when $$$(x, y, 0)$$$ and $$$(x, y, 1)$$$ become connected. This is a classic DSU with small to large merging problem. In short, we drop a token labeled with the index of the query at both $$$(x, y, 0)$$$ and $$$(x, y, 1)$$$. Each time we merge, we also merge the sets of tokens small to large and check if merging has caused two tokens of the same label to be in the same component. The time complexity of our solution is $$$O(nm \log{(nm)} + q\log^2 q)$$$ with the $$$\log{(nm)}$$$ coming from sorting the states or edges. Note that there exists a $$$O((nm \cdot \alpha{(nm)} + q) \cdot \log{(n+m)})$$$ parallel binary search solution as well as a $$$O(nm \log{(nm)} + q\log{(nm)})$$$ solution that uses LCA queries on the Kruskal's reconstruction tree or min path queries on the MSTs. In fact, with offline LCA queries, we can reduce the complexity to $$$O(nm \cdot \alpha{(nm)} + q)$$$.
#include <bits/stdc++.h>
using namespace std;
const int mx = 3e5 + 5, di[4] = {-1, 0, 1, 0}, dj[4] = {0, -1, 0, 1};
int n, m, q, linei, linej, par[mx * 2], ans[mx]; string A[mx];
queue<pair<int, int>> bfsQ; vector<int> dist[mx]; vector<array<int, 3>> edges; set<int> S[mx * 2];
int enc(int i, int j, bool crossParity){
return i * m + j + crossParity * n * m;
}
bool inGrid(int i, int j){
return i >= 0 and i < n and j >= 0 and j < m;
}
int getR(int i){
return i == par[i] ? i : par[i] = getR(par[i]);
}
void merge(int a, int b, int w){
a = getR(a); b = getR(b);
if (a == b)
return;
if (S[a].size() > S[b].size())
swap(S[a], S[b]);
for (int i : S[a]){
if (S[b].count(i)){
ans[i] = w;
S[b].erase(i);
}
else
S[b].insert(i);
}
par[a] = b;
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
cin >> n >> m >> q;
for (int i = 0; i < n; i++){
cin >> A[i];
for (int j = 0; j < m; j++){
dist[i].push_back(1e9);
if (A[i][j] == 'v'){
dist[i][j] = 0;
bfsQ.push({i, j});
}
if (A[i][j] == '#'){
linei = i;
linej = j;
}
}
}
for (int i = 0; i < q; i++){
int x, y; cin >> x >> y;
x--; y--;
S[enc(x, y, 0)].insert(i);
S[enc(x, y, 1)].insert(i);
}
// Multisource BFS to find min distance to volcano
while (bfsQ.size()){
auto [i, j] = bfsQ.front(); bfsQ.pop();
for (int dir = 0; dir < 4; dir++){
int ni = i + di[dir], nj = j + dj[dir];
if (inGrid(ni, nj) and dist[i][j] + 1 < dist[ni][nj]){
dist[ni][nj] = dist[i][j] + 1;
bfsQ.push({ni, nj});
}
}
}
// Get the edges
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
// Look at cells to the up and left (so dir = 0 and dir = 1)
for (int dir = 0; dir < 2; dir++){
int ni = i + di[dir], nj = j + dj[dir];
if (inGrid(ni, nj) and A[i][j] != '#' and A[ni][nj] != '#'){
int w = min(dist[i][j], dist[ni][nj]);
// Crosses the line
if (i == linei and ni == linei - 1 and j > linej){
edges.push_back({w, enc(i, j, 0), enc(ni, nj, 1)});
edges.push_back({w, enc(i, j, 1), enc(ni, nj, 0)});
}
// Doesn't cross the line
else{
edges.push_back({w, enc(i, j, 0), enc(ni, nj, 0)});
edges.push_back({w, enc(i, j, 1), enc(ni, nj, 1)});
}
}
}
}
}
// Sort in reverse and merge to solve offline
sort(edges.begin(), edges.end(), greater<array<int, 3>>());
// Init DSU stuff
iota(par, par + mx * 2, 0);
for (auto [w, u, v] : edges)
merge(u, v, w);
for (int i = 0; i < q; i++)
cout<<ans[i]<<"\n";
}
#include <bits/stdc++.h>
using namespace std;
const int mx = 3e5 + 5, di[4] = {-1, 0, 1, 0}, dj[4] = {0, -1, 0, 1};
int n, m, q, id, linei, linej, par[mx * 4], dep[mx], up[mx * 4][21], val[mx * 4];
string A[mx]; queue<pair<int, int>> bfsQ; vector<int> dist[mx], adj[mx * 4]; vector<array<int, 3>> edges;
int enc(int i, int j, bool crossParity){
// Note that nodes are 1 indexed
return 1 + i * m + j + crossParity * n * m;
}
bool inGrid(int i, int j){
return i >= 0 and i < n and j >= 0 and j < m;
}
int getR(int i){
return i == par[i] ? i : par[i] = getR(par[i]);
}
void merge(int a, int b, int w){
a = getR(a); b = getR(b);
if (a == b)
return;
adj[id].push_back(a);
adj[id].push_back(b);
val[id] = w;
par[a] = par[b] = id;
id++;
}
void dfs(int i){
for (int l = 1; l < 21; l++)
up[i][l] = up[up[i][l - 1]][l - 1];
for (int to : adj[i]){
if (to != up[i][0]){
up[to][0] = i;
dep[to] = dep[i] + 1;
dfs(to);
}
}
}
int qry(int x, int y){
if (dep[x] < dep[y])
swap(x, y);
for (int l = 20, jmp = dep[x] - dep[y]; ~l; l--){
if (jmp & (1 << l)){
x = up[x][l];
}
}
if (x == y)
return val[x];
for (int l = 20; ~l; l--){
if (up[x][l] != up[y][l]){
x = up[x][l];
y = up[y][l];
}
}
return val[up[x][0]];
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
cin >> n >> m >> q;
for (int i = 0; i < n; i++){
cin >> A[i];
for (int j = 0; j < m; j++){
dist[i].push_back(1e9);
if (A[i][j] == 'v'){
dist[i][j] = 0;
bfsQ.push({i, j});
}
if (A[i][j] == '#'){
linei = i;
linej = j;
}
}
}
// Multisource BFS to find min distance to volcano
while (bfsQ.size()){
auto [i, j] = bfsQ.front(); bfsQ.pop();
for (int dir = 0; dir < 4; dir++){
int ni = i + di[dir], nj = j + dj[dir];
if (inGrid(ni, nj) and dist[i][j] + 1 < dist[ni][nj]){
dist[ni][nj] = dist[i][j] + 1;
bfsQ.push({ni, nj});
}
}
}
// Get the edges
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
// Look at cells to the up and left (so dir = 0 and dir = 1)
for (int dir = 0; dir < 2; dir++){
int ni = i + di[dir], nj = j + dj[dir];
if (inGrid(ni, nj) and A[i][j] != '#' and A[ni][nj] != '#'){
int w = min(dist[i][j], dist[ni][nj]);
// Crosses the line
if (i == linei and ni == linei - 1 and j > linej){
edges.push_back({w, enc(i, j, 0), enc(ni, nj, 1)});
edges.push_back({w, enc(i, j, 1), enc(ni, nj, 0)});
}
// Doesn't cross the line
else{
edges.push_back({w, enc(i, j, 0), enc(ni, nj, 0)});
edges.push_back({w, enc(i, j, 1), enc(ni, nj, 1)});
}
}
}
}
}
// We merge from largest w to smallest
sort(edges.begin(), edges.end(), greater<array<int, 3>>());
// Init DSU stuff
id = n * m * 2 + 1;
iota(par, par + mx * 4, 0);
// Merge
for (auto [w, u, v] : edges)
merge(u, v, w);
// DFS to construct the Kruskal's reconstruction trees
for (int i = n * m * 4; i; i--)
if (!up[i][0])
dfs(i);
// Answer queries via LCA queries
for (int i = 0; i < q; i++){
int x, y; cin >> x >> y;
x--; y--;
cout<<qry(enc(x, y, 0), enc(x, y, 1))<<"\n";
}
}










Good round. Had fun solving A, B, C. Kudos for fast editorial!
Thank you for the great contest, the DP recurrence for E was a bit trivial but OK for Div2E.
Thanks for the fast editorial!
Speed Forces!
Thanks all for the super fast editorial
light speed editorial
Problem C: why we take GCD of all value? we can take m=2 to check instead?
It is possible that m=3 works while m=2 doesn't, for example [2, 3], [5, 6] are the same for m = 3 but not m = 2. So you have to use gcd to find the largest m that works.
Thank!
was going to submit b part but time over..matter of seconds lol
Can someone explain to me why O((n+logn)*max divisors of n) is fast enough to pass the tests?
upper bound fornumber of divisors is o(n ^ 1/3) then o(n + logn) * n ^ 1/3) which can be consdered o(n ^ 4/ 3) where the time limit is 3 seconds and n <= 1e5 thats fast enough
The sum of n over all tests does not exceed $$$2 \cdot 10^5$$$, and the maximum divisors a number less than or equal to $$$2 \cdot 10^5$$$ can have is not more than $$$200$$$ (I think it is around $$$160$$$ or something). So in the end this is small enough to pass the problem.
You can practically check that for all numbers $$$N$$$ not greater 200000, the number of divisors is actually $$$O(\sqrt[3]{N})$$$, so the author solution would not take too much operations
No, it's $$$O(e^{\ln(\ln(n))^{1.8}})$$$.
How can you prove this? Thank you in advance!
You can read details here: link
the link doesn't have a proof
Graph is a proof, lol. What proof do you want?
O(f(n)) has definition. You should prove that f(n) satisfy the definition.
may be this is proof by example, they tested it over large number, found the relation between number of devisors verses N, it roughly approximate to O(N^1/3)
There is no such thing as a proof by an example. There is only disproof by a counter example. I believe in the case above there is a proof, it's just not what is linked.
density of primes for given N is 1/log(N) , that relations is also found by only by plotting the graph and there is no exact proof for it...., and we use it very often,
so this relation is also same way found I think...
There is a proof. Several of them. Google "prime number theorem" for more details. "The elementary proof of the prime number theorem: an historical perspective" (by D. Goldfeld) has elementary proof that $$$\pi(n)$$$ is $$$O(\frac{n}{\log n})$$$ on pages 1 and 2 which is really really easy, but this statement is not the same as prime number theorem itself.
There's no sense of proofing it in the context of competitive programming. In every real case the precision of this approximation will be sufficient.
without proof it may be a lie. O() is fact, or not. You can't say it's O() if it's not, except if you ok with a lie. Regarding demands of proof: I didn't demand. I just wanted to stress out that the page doesn't have a proof. And claim that it has a proof is a lie.
it is about 200000*160=3.2*10^8 which can pass in 3 sec
Thanks for fast tutorial.
Wow, Problem C and Problem D are pretty cool. Loved the questions. Thanks !!!!!!!!
Absolutely Correct!!
Loved task B, Thanks for this high quality round.
Hi can u help me out in rectifying the error in this code
if there are more than one occurence of type 3 constraints with the same x,some solutions may be hacked!!
"no two constraints are the exact same." So there can't be more than one occurence of the same type with the same x
i misinterpreted in hurry..thanks
Do you expect people to know that the number of divisors of $$$n$$$ is small in Div2C? It took me a while to realize that you can just check each divisor in $$$O(n)$$$, I bet there were a lot of people who just submitted it without understanding why it works fast
It's a pretty common idea in problems and well known enough
I think most people at least know that the number of divisors is at most 2sqrt(n), and even if you use this extreme bound, O(n sqrt(n)) still passes under the constraints
Oh, forgot about $$$2\sqrt{n}$$$ bound, yes that makes much more sense... I'm now even more ashamed of spending so much time on this problem
For future reference, most of the time it's ok to assume max # of divisors is around N ^ (1/3)
Thanks! I already knew that but apparently not well enough..
You can get the exact bound by finding the number of divisors of the greatest highly composite number less than the constraint. You can find these numbers in this series on oeis https://oeis.org/A002182. These could also be useful when writing tests/hacks for problems.
Okay, I'll bite. how cube root?
What is this 2 root(n) bound about , I am still confused
If $$$d | n$$$ then either $$$d$$$ or $$$\frac{n}{d}$$$ is $$$\leqslant \sqrt{n}$$$ (since $$$d \times \frac{n}{d} = n$$$) so there are no more than $$$\sqrt{n}$$$ divisors that are $$$\leqslant \sqrt{n}$$$ and no more than $$$\sqrt{n}$$$ divisors that are $$$> \sqrt{n}$$$
This was my FIRST Contest ever , I only managed to solve problem A , I tried solving B but could not figure out how would alice calculate which element to remove and which to not? At the end i got frustrated and left.
Honestly I loved the experience.
Who can explain the Kruskal tree method of problem F2, I thought of it for a long time but I don't know how to maintain.
The KRT is a way to solve the subproblem in the editorial where you want to find the largest minimum edge on a path from (x, y, 0) to (x, y, 1). The graph you build on the $$$2nm$$$ nodes is exactly the same (each cell should have two nodes corresponding to the number of times you cross the ray). Then you will run Kruskal's MST algorithm before performing any queries and make a KRT as normal, and the queries will then be the LCA on the KRT between nodes (x, y, 0) and (x, y, 1).
Why does this not work for B? Am I stupid or is this not n log n? Sorry if it's unreadable did the prefix sum backwards.
Thanks for the fast editorial and a wonderful contest!
Damn thought about gcd in C but could not get it. I need to work on my Maths skills lol. Problem B was good.
Explain please, why everyone thinks A, B, C were good? I admit D was nice, though too hard for me. C was unnecessarily hard after incredibly stupid A and a little over-time-consuming B.
Felt the same way for B problem, was kinda of hard for me. Looks like a need some more practice.
In problem C, for the 3rd sample test case (5 11111), the answer given is 2. But the tutorial code gives answer as 1.
We can make a single group of size 5 which will be counted as 1 point. Also we can groups of size 1 and take m as 2, which will also be counted as 1 point.
So,answer should be 2 points. Hence, I think tutorial code is wrong
It gives me 2 when I run it
My bad. Sorry
can anyone tell me why my submission for D got TLE on pretest 3?
arsi[i-1]*(b+1)>=1000000000000000001 i think this can lead to overflow
So I added other constraints (ars[i-1]*(b+1)<ars[i-1]) too.. Can that also lead to overflow..?
I think
ars[i-1]<=1e18/(b+1)is better thanars[i-1]*(b+1)<ars[i-1].When you calculatears[i-1]*(b+1)then it already overflow at some cases and it is possible thatars[i-1]*(b+1)>=ars[i-1]Yes, it may in some cases like in my submission: 241476717. you better use
1e18/(b+1) >= ars[i-1]. I still don't know whyars[i-1]*(b+1) < ars[i-1]can overflow, any explanation is appreciated!Try to run this code:
It overflows, a < 1e18 and result > a. Basic way to find out a similar to this is to solve: $$$x \cdot k = (2^{64}) + x$$$ Solution is: $$$\frac{(2^{64})}{k-1}$$$ I picked $$$k=21$$$ and python with its precision errors:
Fast Editorials :)
Here's an alternate solution to problem C without GCD. Observe that if we need to pick some m such that a set of numbers are all congruent to each other modulo m, m is at most as large as the second smallest element in the set. The bound on m is small enough to bruteforce all k and all m and it somehow works.
Code: 241481077
Excuse me but somehow your submission may TLE when the input is like :
(I wont submit since it's the same as the hack input for #241489844 )
Thanks, good to know! Actually, my solution did get hacked. Seems like the system tests were weak.
I'm not able to observe. Could you please elaborate a bit more on why this works?
Someone send me this solution link in my live stream solution discussion.
I hacked it live there :)
The hack part starts at 1:01:16
Since, you are iterating on all nos until upper, I chose
thing = 2*pandupper = p, where p is a prime.A[n] — 2*A[min(i+x,n)] + A[i] is the Subarray sum. That saves time from O(n^2) to O(n).Prefix sum concept is used.
-2* is because the sum added it already so he needs to subtract it once to get it normal (like without being added to the whole number) without the Bob things, and another time so it gets *-1.
Yes! first X elements are removed from A[n] and bob decrease the sum by negatively adding those x elements again in the sum. But, why does A[i] added again?
the other elements before it? it's a prefix sum. if you basically subtract a number you're subtracting everything before it as well
now I got it. Thank you. i removed elements are not considered to be negatively added again.basically,right x elements of removed elements is bob's negative contribution. Now, I understand it.
I had the idea for B but my implementation was just terrible
Same, took me much time to realize that using a for loop is way better than a while ;-;
was WA on pretest 3 on D meant to catch any known error or just a random case? ;( not able to find my mistake
Alternate Solution to problem C.
For a given divisor of N, its sufficient enough to check if there exists any prime which satisfies the given conditions ( Not so hard to prove why it is so ) . Since there are not many primes under 2.1e5 the solution easily passes for the given constraints . Submission 241489844. Edit: Lmao TL hacked
I have a question how problem C O(n2) solution is being getting accepted ?
I think you mean O(n*(2Sqrt(n))? if you're talking about the gcd.
No, I have seen many solutions which are O(n2) as well. They are getting accepted. How ? They are directly running for loop for findings divisors as well.
241481930 that's my submission, otherwise it's impossible to get accepted I think ;-;
No Worries :) Thank you for sharing your solution
Can you link one such $$$O(n^2)$$$ solution which got accepted?
Sure, Here is that: https://codeforces.com/contest/1920/submission/241451239
damn I thought you were trolling lol, how did this get accepted jfl (he's an lgm tho)
I am also shocked b/w the time limit given was 3 seconds. I think it can get accepted due to that as well.
No that's at most 3e8 I think, turns out it was If(n%k==0) lol
There is a check
if(n%k==0)inside the loop, so the complexity is the same as in the tutorial.Damn fr ;-; so it's O(n*2Sqrt(n))?
Nice :) You are correct Now I observed this thing :) Thanks to you guys !!
This is not $$$\Theta(n^2)$$$.
The inner loop runs only if $$$k$$$ is a factor of $$$n$$$, i.e. $$$d(n)$$$ times, where $$$d(n)$$$ is the number of factors of $$$n$$$.
The inner loop does $$$n-k \in O(n)$$$ iterations; each iteration calls
gcdonce which seems like it would be $$$n \log \max a$$$ in total, but since we calculate gcd with the previous result, the total runtime is $$$n + \log \max a$$$ (check this).Since the above is done $$$d(n)$$$ times, the time complexity is $$$O((n + \log \max a) d(n))$$$. For $$$n \le 2\cdot 10^5$$$, $$$d(n)$$$ is at most $$$160$$$ (this is reached for $$$n = 196560$$$; you can verify it yourself if you wish). This is fast enough.
there's the check part n%i
can any one give me explanation of problem B?
You need to find the maximum possible answer, after both alice and bob playing for one round, Alice, will try to remove K numbers at most to maximize the answer, and Bob will make X numbers negative to minimize the solution thus he'd choose the greatest numbers cause their negatives is the smallest.
I can't justify my D-time complexity. this is my D
solution for problem D**
https://codeforces.com/contest/1920/submission/241488534
No it was a joke nvm lol
https://codeforces.com/contest/1920/submission/241478736 what is wrong in this code for problem C?
can someone explain ans = max(ans, A[n] — 2 * A[min(i + x, n)] + A[i]); in part b?
Since he added the sum, and wants to subtract it for bob part. he multiplied it by 2 so it subtracts not just not do anything... and he is getting the max, since Alice (Idk if I am saying the names flipped lol) wants to maximize the solution
y why does he multiply by 2?
Cuz he got the sum the first time Let's you have two numbers 1 and 2, if you want to multiply 2 by -1 after you takte the sum, the sum being 3. 3-2=1--> this is the first time you didn't multiply 2 by -1 you her just got back to the starting point 1-2 (multiplication by 2) = -1.
Here is an alternative solution for F1 (in practice: 241489058).
First, run a multi-source BFS from all volcanoes to determine the distance from every square to the nearest volcano.
Now, given a query, we run another kind of BFS from the given square. Let $$$d$$$ be the distance from this square to the nearest volcano. Instead of one queue, we maintain $$$d + 1$$$ queues: the squares reachable when the minimum distance to the volcanoes is $$$0, 1, 2, \ldots, d$$$. Initially, the $$$d$$$-th queue contains our starting square, and we process the queues in the order from highest to lowest.
The remaining issue is to detect when we made a turn around the island. For that, pick an arbitrary square of the island in advance. For each visited square, maintain a real value: how the polar angle changed when getting to that square. When the square was not yet visited, just record the current value. When we arrive at an already visited square: if the difference between the old and the new value is close to zero, do nothing; but if it is not (most probably close to $$$\pm 2 \pi$$$ then), we just found a round trip. What remains is to record the greatest possible distance from volcanoes when this happened.
Can someone please explain in problem B why nlogn is passing? Because number of testcases are 1e4 and n is 1e5 and k<=n so when k=1 and n=1e5 and t=1e4 will the nlogn solution will be accepted?
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2\cdot 10^5$$$.
Oh got it thanks
Am I the only one who found majority of the problems in this contest to be filler?
F2 can be solved in $$$O(nm\cdot\alpha(nm)+q)$$$ with offline LCA.
Hey,
I think the data for Problem C might have been a little weak. The following testcase:
Can hack solutions which use the heuristic that the GCD should be = 1 (if more than 1 then that GCD value itself works), and also that the only valid answer is 49999 (which is a large prime). Some solutions try all numbers from $$$2...10^5$$$ and that should usually be too slow, I think.
Thanks!
precompute divisors SMH
Thanks for the clear and short conditions!
I personally think C is harder than D. Maybe swap them is better?
I misunderstood E's "substring" as "subsequence" and wrote a wrong DP.Now feeling I'm a noob :(
it happens (I'm actually a noob)
Can someone kindly
helpwith any simple test case forProblem D, for which my solution fails? Or, help me identify what mistake in my code (in Java — 241492905) ?Negative time to editorial publish
For problem C: I Need some help to figure out what the complexity of this solution is: 241500814
It might be around O(N*log(N)) I guess, but I am not sure.
So, what I did is to first arrange all factors of n in a 2D vector (let's say V) s.t.
in any vector if the elements are like {a,b,c... x,y} then it holds that b%a=0, c%b=0.... y%x=0.
Once we have such arrays we can binary search on each of them to find out for how many of the factors in an array m>1 exists.
So if the size of this 2D vector is X, then the complexity would be something like: O(N*log(N)*X), but what will be the upper bound on X??
n^1/3
C was a bit standard, but great contest overall.. thank you.
Its not necessary to use prefix sum for problem B ryt?
This was a good round, but the only issue I had was that D had repeated occurrences of indices. I know it was never stated in the input that the indices had to be distinct, but I felt like it was obvious enough to assume haha. Well, at least I learned to be a lot more careful.
I do think that at least one of the examples should have featured repeated indices though.
you cant expect samples to cover everything, and in this case, repeated indices isnt an edge case for 99.9% of solutions
Today's contest had way stronger samples than usual (and imo way stronger than should be)
Please Anyone help me Find out Why my Solution is failing on some testcases! Problem D — My submission — 241508049
Please, someone, i beg you, tell me why this C++ solution fails Problem D test 3 241505744 . The same exact solution works in python. There were size issues in the beginning but i addresses them. Now I just don't know what it could be and i've been trying to fix this for over 3 hours. (the python was almost correct more than 3 hours ago, but after realizing the potential size of the accumulated array can be >>>>> 10**18, i made a small adjustment and it worked). But the c++ just won't and i'm just super frustrated... please :(
I'll just say briefly, there is a "recursive" class that holds the old array before multiplying (type 2 operation) by a factor, and it also holds the additions (type 1 operatoin) that happened since the last multiplication.
241515808 please tell why is it giving run time error
Excellent round. C is good and standard. However I stuck in the gap between C and D so the round go speedforces for me :(((((
1920B — Summation Game Follow this step. I think it will help to you : Input Handling , Sort, Calculating Initial Sum, Iterating to Maximize Sum and output here code -> https://ideone.com/kXKZYF
use GCD for c number problem
yep you are right i also done this problem using __gcd. Thank You for sharing your idea
thankyou dear.❤️
okk
That was an amazing contest with some cool problems like C and E
Problem C was cool, I learned so much
Good round!
Can anyone explain why calculating gcd of series of numbers take n+logn and not nlogn time
Although i solved ABC but i wasn't aware of this
If $$$gcd(a, b) = a$$$ or $$$gcd(a, b) = b$$$, the gcd algorithm will be $$$O(1)$$$. Furthermore, when we do cumulative gcd of all the numbers, our current gcd can only decrease $$$O(\log n)$$$ times (if it doesn't decrease, we have the case previously mentioned which is constant), which is why the check function runs in $$$O(n + \log n)$$$.
Thanks for the reply
Problems were good hope to see more contests from you in future
Problem C but with better time complexity. Haven't proved it mathematically but I think time complexity is n*log(n). Uses the fact that if 1, 2, 4, 8, ... are factors of 2^k == n than in worst case we need to check no more than 2^k + 2^(k-1) + 2^(k-2) ... which is 2*n numbers. And assuming gcds check are log(n) hence ig n*log(n). But math gets complicated when n is not pure power of any prime. So ig I will leave it for someone else.
https://codeforces.com/contest/1920/submission/241529452
We can modify your code to slow down, but it will be easier to estimate.
Lets describe changes. We always use all primes of initial n. We check
k >= mnonly after gcds. This makes our code always calculate for gcd for each prime factor (not only larger ones). We checkn % k == 0, because it may not happen in this version. We start withi = 0, this makes few uselessg = gcd(g, 0)calls, but this is easier to estimate.Those modifications makes eval be called for each divisor of initial $$$n$$$, and single call without recursive calls takes $$$O(prime.size()\cdot (n + \log(\text{initial_n})))$$$, here $$$n$$$ is what passed into function. We can estimate $$$prime.size()$$$ as a $$$\log(n)$$$.
So, overall complexity is:
There are two common definitions:
So, we get $$$O(\log(n)\sigma(n) + \log^2(n)d(n))$$$. Next, we can plug in some upper bounds. For example:
Plug in those:
Simplify, using rules of big O notation.
Leave a comment if you found mistakes.
Non-modified code is faster. But it's really hard to estimate its complexity. And if you use
k <= mninstead, it even more faster. Because it reduces size of n by larger factors first.Thanks For the analysis <3
Damn, I didn't see the constraints for 1920B - Summation Game and solved by considering negative numbers as well XD, submission.
First approach of problem D is really new learning to me. Thanks.
Can anyone explain what is wrong in this code for D 241534324
The editorial for F2 says that the time complexity of parallel binary search solution is $$$O((nm\cdot \alpha(nm)+q)\cdot (n+m))$$$. Here the $$$\alpha(nm)$$$ should from path compression in dsu, but I think we cannot use path compression since we need undo the operations, or can we?
My parallel binary search solution just uses a regular DSU. You do $$$O( \log(n+m) )$$$ rounds of incrementally adding all potential edges between neighbours at the right times. At a certain point in this sweep you do one connectivity query for each of the queries, no need for undoing: 241434298 The only thing that does not quite achieve this time complexity is some sorting I call inside the parallel binary search, but it can of course easily be fixed.
That makes sense. Thanks very much.
Problem C
For people who didnt get why taking the gcd of difference of nos at all those positions works (found it a pretty cool idea):
Consider all the first nos from all partitions as:
a1, a2, a3, a4, .. , akNow if they have a difference which is multiple of a common number G, they can be written as: (say)
a1, a1+3G, a1-4G, a1+103G, .. , a1+7GNow for
m=Gyou get the same remainder for this sequence:a1%GNow for the same no to appear at all such positions in all partitions, the required
mwill be thegcdof differences at all such positions.I hope it makes sense now!
Can someone please explain the formula used in B solution in the editorial? I cannot wrap my head around it. Thanks in advance.
Apparently goes like this. Let e be the element of the arr, r be the rest of the sum.
To find the difference of sum. S = e+r S' = -e+r
S'-S = (-e+r)-(e+r)= -2e
thanks alot!
in problem c can someone tell that cant we just find all prime number lenghts(k) satsifying the condition (i.e m>=2) and then like we do in sieve find all the multiples of those lenghts and that will be the ans,TC of it will be n logn but idk why this approch 241560669 is failing
[1,1,2,2,1,1,2,2] can't be split on any primes, but does split on k = 4.
https://codeforces.com/contest/1920/submission/241572267
Can someone explain why this solution of task D gets accepted on visual c++ 2017, and gets a time limit on g++20?
Hey! can someone please help me out with how to calculate the time complexity for Problem C. My doubt is why is not the code in the solution given not throw TLE, The code looks like a O(n^2) solution
When we check some divisor $$$k$$$, it will take $$$O(n + \log n)$$$ time since we are taking cumulative gcd of $$$O(n)$$$ numbers. The reason why the code does not take $$$O(n^2)$$$ is because the number of divisors $$$x$$$ can have if $$$1 \leq x \leq 2\cdot10^5$$$ is pretty small, around 160. So the actual time complexity is closer to $$$O(n \cdot max divisors)$$$.
Had a doubt regarding problem D, would appreciate any help I could get for the same!
In the editorial I can see that they have used 2e18 as the upper limit, but since the max length index is 1e18, having (1e18+5) would work as well right?
I did something similar during the (virtual) contest, but initially gave 1e18+5 as the upper limit, which failed. then I gave 2e18+5 as the upper limit, and voila! it passed! Funny thing is that the test case it failed on didn't fail on my local with 1e18+5 limit!
Now I know that happens alot that a solution would fail on one IDE and pass on another, but I was unable to figure out why that happened in this case, any pointers would be highly appreciated!
Failed solution — https://codeforces.com/contest/1920/submission/241579138
Accepted solution — https://codeforces.com/contest/1920/submission/241583879
( PS : I know my both my solutions should have given TLE for a particular edge case, but I guess CF problem setters didn't think someone would be as stupid as me :P )
1e18 will work for python, but cpp compiler cant precise the float value after big division(in my case), ex 1223333444333332.13 gives something like 12.23e14 or something, so the condition falls for that limit, so u have to take more bigger value
What's the time complexity in C?O(n*n)
can anyone help me with my approach for problem d ?
for op 2 I incremented x by x=(x-1)*(a+1)+1 (index of the next element) for op 1 I put the value in map map[x]=value and used lower bound to find the index in map and if not found then used while loop until found edit: solved it, didn't use the limit of 1e18 here is ac code 241701574
Can someone tell my why my Python code is getting a TLE for C. The logic seems identical to the C++ answer
Python 3 is too slow. Use PyPy3 to submit your code.
Your accepted solution.
https://codeforces.com/contest/1920/submission/241625518 Can anyone tell what is the problem with this submission? It is giving correct answer in my PC. But i guess while checking overflow there is a problem.
I have solution for 1920F2 - Smooth Sailing (Hard Version) in $$$O(nm\cdot\alpha(nm) + q)$$$.
It's basically similar idea as in the editorial. But... with a few differences.
First one: instead of parity, I'm using angles. I think you can exchange those. So, in DSU I maintain for each node angle to its root, if I walk there cell by cell in MST. Then, to check is there round trip I check all cycles if total angle of circle > pi / 2. Why pi / 2? Well, I thought it's enough :D
Seocond one: why is the complexity different? Well, each time I find a cycle I answer on all cells within the component. Not taking into account are they listed in queries or not. How do I keep list of cells within a component? I maintain other tree -- binary tree with new node added when two component joined, and this node I have two children representing joined components. In this way I can use dfs to traverse all cells within component. And after I do it, I clear list of component cells, it's same as marking component as having round trip. First I thought to make linked list, but I thought it would be troublesome.
So, complexity consists of: $$$O(nm)$$$ joins in DSU, which leads to $$$O(nm\cdot\alpha(nm))$$$ and traversing components when cycle is found, which is $$$O(nm)$$$. Calculating angles adds time for calculating arc sin, but you may consider it as a constant. If you dislike it, you can use parity approach I guess.
Here is the code 241633554
Here is parity version: 241636798
How does the editorial for problem F2 account for a case like this?
https://imgur.com/a/W2gRkVa
Round trip is a loop. We consider only loops. In vertical segment you have on pic, you would have to go up and down, or down and up, thus there is 3 intersections of round trip on the pic (if it's cycle).
Thank you for your reply. I'm still confused about how there are 3 intersections to the right of the island — aren't we just counting how many blocks cross the dotted line? Additionally, how are we keeping track of if a component forms a round trip (or polygon) ?
First, we use idea about odd number of intersections as a fact. If you're not convinced, look for information in the internet about checking whether point lies inside polygon.
Next, we rephrase this criteria as follows: pick any loop with island inside. Pick any starting point on it. Let $$$p_1, p_2, p_3 \dots p_n$$$ to be points on the loop in order of round trip. Here $$$p_n = p_1$$$. Then, we define parity of index $$$i$$$ as the parity of intersection of the path $$$p_1,p_2...p_i$$$. We tie parity to index because points may coincide (ending points for example). Then, parity of index n should have 1.
This shows us that if loop exists, then there is path from point to the same point but with parity 1. Similarly, if we assume we start with parity 1, then there is path to parity 0.
Next step, we claim that this is not just "if then", but "if and only if". In other words. If there is a path from 0 to 1 to the same point, then there is a loop with odd number of intersections. For some (like me) it seems obvious. But I'll explain it anyway.
Suppose we have a path $$$p_1,p_2,p_3\dots p_n$$$ where $$$p_1 = p_n$$$ and parity of index 0 is 0 and parity of index $$$n$$$ is 1. Then, if you forget about parity, then it is a loop, because $$$p_1 = p_n$$$. But if you recall about parity, then it has odd number of intersections.
In other words, existence of path $$$\leftrightarrow$$$ existance of a round trip. Next, step... existence of path is the same as reachability. But to find out this kind of reachability, we define new graph. It has triples as a vertices. $$$(x, y, parity)$$$. So, for each original point, there are two "duplicates": $$$(x, y, 0)$$$ and $$$(x, y, 1)$$$. Then, all points are connected as before, except, if a single step from $$$(x_1, y_1, p_1)$$$ to $$$(x_2, y_2, p_2)$$$ crosses the line above certain rock cell, then $$$p_1 \neq p_2$$$ (parity changes). Otherwise $$$p_1 = p_2$$$.
Then, if we have a path from $$$(x, y, 0)$$$ to $$$(x, y, 1)$$$ in this new graph then there is a round trip we want to find. Having path = reachability. So, if $$$(x, y, 0)$$$ and $$$(x, y, 1)$$$ within the same component, it means $$$(x, y, 1)$$$ is reachable from $$$(x, y, 0)$$$ and thus there is a round trip we looking for. Then, to answer a question about a given starting point, we should check is there some pair $$$(x, y, 0) (x, y, 1)$$$ within the same component as the given point.
What about a distance we asked for? Well, we start from maximum distance, and decrease it. Each step we allow to walk in cells which has lower and lower distance, merging them in DSU which maintain reachability components.
very helpful!
in Problem C ,if m is gcd of m1,m2,... then all the divisor of m will also satisfy the condition of partitioning the array, then why we have only added 1 to our answer, we should add the count of divisor of m. If I am wrong please correct me?
All the divisors of m also satisfy the condition, but that is only for a particular k. We add one point for each k for which there exists m >= 2.
I have another solution to F2 in $$$O(nm \cdot min(n, m))$$$ that doesn't use small to large or LCA.
My solution follows the editorial up to drawing the imaginary line. Then, I process all of the edges except those that cross the line in order of decreasing $$$d$$$.
After adding each edge, create a graph where the components in the DSU are nodes. For each edge that crosses the line, add an edge between the corresponding nodes. If there is a cycle of odd length in this graph, then that cycle and all nodes connected to it form a round trip (basically the same observation as in the editorial). We can now merge all of these nodes and make a note that this component is a round trip in the DSU.
If we choose our line correctly (either horizontally or vertically), this solution runs in $$$O(nm \cdot min(n, m))$$$. My code passes in 580 ms.
In D if solving by repeated binary search according to the editorial why is there dp[i]=((v+1)>2e18)? (ll)2e18: dp[i-1]*(v+1);
if i am doing dp[i]=dp[i-1]*(v+1) directly its giving wrong answer. can someone explain.
For B a more verbose sol. 242411746
Only reason "" pref[n] — 2 * pref[min(i+x,n)] + pref[i]"" works is because the prefix array starts with 0.
I hope someone finds it helpful. Because I got bricked reading that.
The LaTeX rendered like this, initially I thought it was something nobody bothered to fix.
Recently I found out that it is a Chrome issue — https://affinemess.quora.com/A-brief-PSA-about-reading-math-on-Quora
Can anybody the problem with my solution for Problem C ?
Can anyone please tell me why my code for problem D isn't working , it's working for small test cases but gives wrong answer for the 3rd example test case with big integers
Problem C was very intuitive. Loved the problem
why is time complexity of problem C { n+ log(n) }* max.diviosrs(n) and not n*log(n)*max.divisors(n) ?