Hi everyone,
Well, I've been struggling with this problem for a while. The greedy approach is incorrect and there is a quite straightforward O(N^2) dp solution which will obviously not run in time. I gave up and tried to find solutions online but I couldn't find anything but a topcoder topic where there were some hints. If anyone can explain the solution of this problem it would be great.











Hi,
I like trying to decompose and explain things because that is usually a very good way to help you (as the person trying to explain something) understand the subject better and forge new connections inside your brain about how different pieces of different puzzles may relate to each other. In addition, I solved this problem not very long ago, so I still have a somewhat fresh memory of the process I went through when I solved it, so I'll try to contribute my perspective, hoping it will be helpful.
First of all, for those who may find it interesting and haven't read this problem before, here's the problem statement: Save the Trees.
Okay, I'll try to present the key elements of my approach as briefly as possible. Let's start with a few definitions to help model the solution. Let's denote the ith tree in the sequence as Ti, and let's define a function S that represents the solution to the problem, up to a certain tree:
S(n): The minimum possible price for the group of trees {T1, T2, ..., Tn}.
This means solving the problem is equivalent to calculating S(N). Okay, now let's define another simple function G that points to a certain place in the sequence of trees, and helps us know where to partition the sequence into valid groups:
Gn: The lowest index possible such that the group of trees {TGn, TGn + 1, ..., Tn} form a valid group—i.e. no two trees inside that set have the same type.
To help illustrate this, let's consider a small group of 7 trees as follows (ti denoting the type of Ti):
t = {1, 2, 3, 2, 4, 3, 5}
In this example, for the third tree (T3) we have t3 = 3, G3 = 1, which means that you can form a valid group starting in tree 1, and ending in tree 3. Other examples would be t4 = 2, G4 = 3 and t7 = 5, G7 = 4. I hope it is clear. Now, one more definition:
H(i, j): the height of the tallest tree in the group {Ti, Ti + 1, ..., Tj}.
Okay, so we are interested calculating S(n), assuming that we have already calculated S(1), S(2), ..., S(n - 1). It should be easy to see that in order to involve Tn in our new calculation, we may have to partition the trees and put Tn in a group of trees that can't go beyond TGn. That is, the solution S(n) has to come from S(Gn - 1) + H(Gn, n), or S(Gn) + H(Gn + 1, n), or S(Gn + 1) + H(Gn + 2, n)... etc. To put it more formally:
Now, of course calculating all those values (I mean, for all those k) may be done in naive ways, with complexities O(n) or worse, but it may also be done in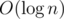 if you use a proper data structure, like a segment tree, for example.
if you use a proper data structure, like a segment tree, for example.
I think I have outlined now all the key elements to the method I personally used to solve this problem. My solution iterates over the trees sequentially, and uses two segment trees, one is an auxiliary tree to help me calculate H and the other has the values S(k), H(k + 1, n), and of course S(k) + H(k + 1, n) for every index k in the sequence—this second segtree was the trickiest because it contains three values in each node. These trees get updated for every n, from 1 to N, and in the end the solution for the whole problem comes out.
I'm leaving some implementation details out, but I think this should be enough so that you can formulate your own strategy and write a solution according to your way of reasoning. If you any questions, though, feel free to ask :).
Best of luck.
Thanks a million for your great explanation, I really appreciate the time and effort you put into writing this. I liked the way you decomposed the problem, pretty neat :)