Hi Codeforces!
Have you ever had this issue before?

If yes, then you have come to the right place! This is a blog about my super easy to use template for (reroot) DP on trees. I really believe that this template is kind of revolutionary for solving reroot DP problems. I've implemented it both in Python and in C++ (the template supports Python2, Python3 and >= C++14). Using this template, you will be able to easily solve > 2000 rated reroot problems in a couple of minutes, with a couple of lines of code.
A big thanks goes out to everyone that has helped me by giving feedback on blog and/or discussing reroot with me, nor, meooow, qmk, demoralizer, jeroenodb, ffao. And especially a huge thanks goes to nor for helping out making the C++ version of the template.
1. Introduction / Motivation
As an example, consider this problem: 1324F - Maximum White Subtree. The single thing that makes this problem difficult is that you need for every node $$$u$$$ find the maximum white subtree containing $$$u$$$. Had this problem only asked to find the answer for a specific node $$$u$$$, then a simple dfs solution would have worked.
But 1324F - Maximum White Subtree requires you to find the answer for every node. This forces you to use a technique called rerooting. Long story short, it is a mess to code. Maybe you could argue that for this specific problem it isn't all that bad. But it is definitely not as easy to code as the dfs solution above.
What if I told you that it is possible to take the logic from the dfs function above, put it inside of a "black box", and get the answer for all $$$u$$$ in $$$O(n \log n)$$$ time? Well it is, and that is what this blog is all about =)
In order to extract the logic from the simple dfs solution, let us first create a generic template for DP on trees and implement the simple dfs solution using its interface. Note that the following code contain the exact same logic as the simple dfs solution above. It solves the problem for a specific node $$$u$$$.
Now, all that remains to solve the full problem is to switch out the treeDP function with the ultimate reroot template. The template returns the output of treeDP for every node $$$u$$$, in $$$O(n \log n)$$$ time! It is just that easy. 240150867
The takeaway from this is example is that the reroot template makes it almost trivial to solve complicated reroot problems. For example, suppose we modify 1324F - Maximum White Subtree such that both nodes and edges have colors. Normally this modification would be complicated and would require an entire overhaul of the solution. However, with the ultimate reroot template, the solution is simply:
2. Collection of reroot problems and solutions
Here is a collection of reroot problems on Codeforces, together with some short and simple solutions in both Python and C++ using the rerooter template. These are nice problems to practice on if you want to try out using this template. The difficulty rating ranges between 1700 and 2600. I've also put together a GYM contest with all of the problems: Collection of Reroot DP problems (difficulty rating 1700 to 2600).
- (1700 rating) 219D - Choosing Capital for Treeland
- Python solution, C++ solution
- (2300 rating) 543D - Road Improvement
- Python solution, C++ solution
- (2200 rating) 592D - Super M
- Python solution, C++ solution
- (2600 rating) 627D - Preorder Test
- Python solution, C++ solution
- (2100 rating) 852E - Casinos and travel
- Python solution, C++ solution
- (2300 rating) 960E - Alternating Tree
- Python solution, C++ solution
- Or alternatively using "edge DP":
- Python solution, C++ solution
- (1900 rating) 1092F - Tree with Maximum Cost
- Python solution, C++ solution
- (2200 rating) 1156D - 0-1-Tree
- Python solution, C++ solution
- (2400 rating) 1182D - Complete Mirror
- Python solution, C++ solution
- (2100 rating) 1187E - Tree Painting
- Python solution, C++ solution
- (2000 rating) 1294F - Three Paths on a Tree
- Python solution, C++ solution
- (1800 rating) 1324F - Maximum White Subtree
- Python solution, C++ solution
- (2500 rating) 1498F - Christmas Game
- Python solution, C++ solution
- (2400 rating) 1626E - Black and White Tree
- Python solution, C++ solution
- (2500 rating) 1691F - K-Set Tree
- Python solution, C++ solution
- (2400 rating) 1794E - Labeling the Tree with Distances
- Python solution, C++ solution
- (2500 rating) 1796E - Colored Subgraphs
- Python solution, C++ solution
- (1700 rating) 1881F - Minimum Maximum Distance
- Python solution, C++ solution
- 104008G - Group Homework
- Python solution, C++ solution
- 104665H - Alice Learns Eertree!
- Python solution, C++ solution
3. Understanding the rerooter black box
The following is the black box rerooter implemented naively:
rerooter outputs three variables.
rootDPis a list, whererootDP[node] = dfs(node).forwardDPis a list of lists, whereforwardDP[node][eind] = dfs(nei, node), wherenei = graph[node][eind].reverseDPis a list of lists, wherereverseDP[node][eind] = dfs(node, nei), wherenei = graph[node][eind].
If you don't understand the definitions of rootDP/forwardDP/reverseDP, then I recommend reading the naive $$$O(n^2)$$$ implementation of rerooter. It should be fairly self explanatory.
The rest of this blog is about the techniques of how to make rerooter run in $$$O(n \log n)$$$. So if you just want to use rerooter as a black box, then you don't have to read or understand the rest of this blog.
One last remark. If you've ever done rerooting before, you might recall that rerooting usually runs in $$$O(n)$$$ time. So why does this template run in $$$O(n \log n)$$$? The reason for this is that I restrict myself to use the combine function in a left folding procedure, e.g. combine(combine(combine(nodeDP, neiDP1), neiDP2), neiDP3). My template is not allowed to do for example combine(nodeDP, combine(neiDP1, combine(neiDP2, neiDP3))). While this limitation makes the template run slower, $$$O(n \log n)$$$ instead of $$$O(n)$$$, it also makes it a lot easier to use the template. If you still think that the $$$O(n)$$$ version is superior, then I don't think you've understood how nice and general the $$$O(n \log n)$$$ version truly is.
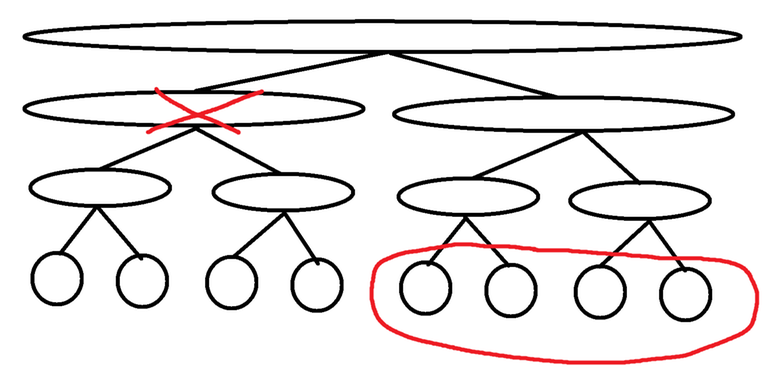
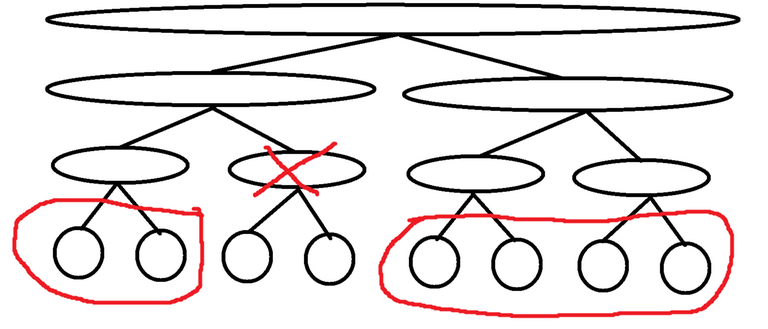
4. Rerooting and exclusivity
The general idea behind rerooting is that we first compute the DP as normal for some arbitrary node as the root (I use node = 0 for this). After we have done this we can "move" the root of the tree by updating the DP value of the old root and the DP value of a neighbour to the old root. That neighbour then becomes the new root.
Let $$$u$$$ denote the current root, and let $$$v$$$ denote the neighbour of $$$u$$$ that we want to move the root to. At this point, we already know the value of dfs(v, u) since $$$u$$$ is the current root. But in order to be able to move the root from $$$u$$$ to $$$v$$$, we need to find the new DP value of $$$u$$$, i.e. dfs(u, v).
If we think about this in terms of forwardDP and reverseDP, then we currently know forwardDP[u], and our goal is to compute reverseDP[u]. This can be done naively in $$$O(\text{deg}(u)^2)$$$ time with a couple of for loops by calling combine $$$O(\text{deg}(u)^2)$$$ times, and then calling finalize $$$O(\text{deg}(u))$$$ times.
The bottle neck here are the $$$O(\text{deg}(u)^2)$$$ calls to combine. So for now, let us separate out the part of the code that calls combine from the rest of the code into a function called exclusive. The goal of the next section will then be to speed up the naively implemented exclusive function to run in $$$O(\text{deg}(u) \text{log} (\text{deg}(u)))$$$ time.
5. The exclusive segment tree
We are almost done implementing the fast reroot template. The only operation left to speed up is the function exclusive. Currently it runs in $$$O(\sum \text{deg}^2)$$$ time. The trick to make exclusive run in $$$O(\sum \text{deg} \log{(\text{deg})})$$$ time is to create something similar to a segment tree.
Suppose you have a segment tree where each node in the segment tree accumulates all of the values outside of its interval. The leaves of such a segment tree can then be used as the output of exclusive. I call this data structure the exclusive segment tree.
The exclusive segment tree is naturally built from top to bottom, taking $$$O(n \log n)$$$ time. Here is an implementation of rerooter using the exclusive segment tree:
This algorithm runs in $$$O(\sum \text{deg} \log{(\text{deg})})$$$, so we are essentially done. However, this implementation uses recursive DFS which especially for Python is a huge drawback. Recursion in Python is both relatively slow and increadibly memory hungry. So for a far more practical version, I've also implemented this same algorithm using a BFS instead of a DFS. This gives us the final version of the ultimate rerooter template!











God tier blog!
There is one minor point that confused me a bit: "Only-left folding" refers to only accumulating values of dp from child to parent, and not allowing combining between various children. It does not demand that the children are always processed in the same order. Of course, no problems I have solved ever violated this assumption.
I would like to mention something similar that I have been using: In the blog you basically explained two options, but I usually do the third option:
The third option, in the terminology of your blog, it would be making both a combine and De-combine function. This option is much closer to typical implementation of a reroot tree DP. Sum and Xor can be easily reversed. Children max are a bit more difficult but can be achieved by keeping two maximum values. Thus this is easily O(n). Most of the time, the reverse function is, well, exact reverse of the combine function. Comparing the first option and the third option, this saved the $$$\log $$$ by double code length of the combine function, so it could be worth it -- doubling something two to three lines isn't really so bad.
It is a shame that there is no perfect template that does not have to give something up. It is also unfortunate that all three methods used slightly different representations so it is hard to code all three of them in the same template.
Speaking about that. We (me and nor) have made many different versions of the template. For example we have a version that supports an optional de-combine argument.
If you are interested in that, then take a look at these two C++ submissions 240160904, 240160922. The first submission calls rerooter without a de-combine function (running in $$$O(n \text{log} (n))$$$). The second submission calls rerooter with a de-combine function (so it runs in $$$O(n)$$$ time).
Here is what I've noticed after solving a ton of reroot problems on Codeforces.
I've yet to find a reroot problem where C++ TLE's with the $$$O(n \text{log} (n))$$$ template. In fact, using Python I've only TLEd once (on problem 627D - Preorder Test).
I usually don't see that big of a speedup going from $$$O(n \text{log} (n))$$$ to $$$O(n)$$$. This might be because the worst case input (a star) is missing from the test data. Note that for random trees (ish bounded max degree), even the $$$O(n \text{log} (n))$$$ version of the template runs in $$$O(n)$$$.
In case someone finds the BFS non-intuitive (you should definitely check it out by the way, it's really cool), and prefer keeping a DFS in your template in the off-chance that you need to modify the template (which should happen very rarely if not never), here are two submissions with the DFS template we came up with: 240165750 and 240165755.
Note that this will have very similar speed to the BFS template, but in terms of memory usage, this takes more memory than BFS due to recursion. It has never been an issue in all the problems we've seen, but the memory overhead is somewhat significant, so don't get rid of your BFS template in case you encounter a problem with a tight ML.
Is it really safe to append to the list you are iterating over in python?
Surprisingly (for C++ users) yes. Iteration in Python is a completely different beast from what we assume in C++ — iterators are much more complicated in terms of book-keeping (even iteration itself is done by catching an exception each iteration).
From what I understand, the answer to that is yes. In general, standard library data-structures in Python throw exceptions if it isn't ok. Take for example
It throws an exception:
RuntimeError: set changed size during iteration.I'm personally a huge fan of appending to lists while iterating over them. It runs very fast, and it makes coding BFS super easy. Probably my favourite Python algorithm ever is this BFS algorithm I made for trees
One of the reasons why this is so nice is that you can reuse the
BFSlist. For example, if you want to computesubtree_size, then you can just add on1) more problems:
592D - Super M
1156D - 0-1-Tree
1332F - Independent Set
2) as I see your template not works with forests. might be useful here:
1101D - GCD Counting
ABC248G
3) by my experience exlusive on c++ works faster with recursive version instead of bit magic version. is this ok (nor)?
4) why this template requires 3 lambdas? As I know with 3 we can acheive $$$O(n)$$$ time and advantage of this $$$O(nlogn)$$$ method that we need only 2 lambdas to describe. I didn't solve all problems yet, do I miss something?
Can you share the recursive version you're using?
full code: 240168593 (1825 ms)
same code but with exclude from blog: 240203678 (3000 ms)
I tried using this in the template in the blog. The performance gains seem insignificant if you think about the granularity of CF timing (the gain is around 2 times the least count of the timer that CF uses), so in another submission, it might as well may perform worse than the submission in the blog.
Template: https://codeforces.com/contest/960/submission/240131037
Template but recursive exclusive: https://codeforces.com/contest/960/submission/240230032
It is nowhere near the difference that you showed in your submissions. The drastic difference in your submissions is most likely because of the fact that you allocate the vector and copy its contents, on top of doing the same work that the recursive code is doing (allocations are very costly and can easily overpower an O(n log n) algorithm in terms of cost).
Why you tried on task where input takes probably half of the time and solution are fast? :D
Nuh, allocations are nothing. Atleast I moved allocation of vector out of lambda and nothing changes. I think recursion is more cache friendly.
I submitted on the same problem, and the results didn't change with our template.
Template (3119ms): https://codeforces.com/contest/627/submission/240130592
Template but recursive exclusive (2931ms — 7% better, probably not significant, my other submissions on the same problem have a large variance, plus with larger execution times, time variance tends to be higher): https://codeforces.com/contest/627/submission/240232312
Template but without explicitly returning/storing all of edge_dp/redge_dp (1606ms — 2x speedup): https://codeforces.com/contest/627/submission/240234284
On a quick skim of your submissions, I am not exactly sure where the bottlenecks are, but you don't seem to be computing edge_dp/redge_dp, so there is no one-to-one correspondence between your submission and the submissions using this template — in all likelihood the 1606ms submission is the one you should be comparing your submission to.
On the gap between your submissions — it might be possible that
a[i]is a very bad order for the cache. But in my experience, allocations are much more unpredictable and can take arbitrary amounts of time — this comes from doing some serious constant-optimizations and getting fastest solutions on online judges. It is especially bad when you do many small vector allocations, for example, the code that takes 1606ms also doesn't do repeated allocations (i.e., calls toreserve) that we were doing earlier.Also, if you care about performance, I would recommend not using
std::functionunless you really need type erasure for things like storing lambdas in a vector (in which case you can just convert a lambda tostd::functionwhich is easy to do).I've added 592D - Super M and 1156D - 0-1-Tree to the list. But, I'm not sure why 1332F - Independent Set should be considered a reroot problem. As far as I can tell it is just a standard tree DP problem.
I agree that it might be nice to add support for forests to the template. Doing that would at the same time add support for 1-indexing. But, it would also make the template itself more complicated.
pajenegod could you please explain the specific purpose of merge_into, finalize_merge and base in the cpp template? Thank you.
Here is a step guide for how to use the reroot template. I will use 1324F - Maximum White Subtree as an example.
240150867
240131453
sorry, messed up the input format. i wish cf had an option to delete comments
Me wondering when did I ever discuss rerooting with pajengod orz sir. (probably 2-3years ago on AC or Errichto discord server)
Yeah. I initially started working on this blog like 2 years ago. Sometimes around that time, I remember discussing it with you over on the AC server. I never finished it back then. But this year I had some spare time of Christmas so I decided to finally finish up the blog.
Setters for the next round are shrivelling in fear that their rerooting problem will get DESTROYED by The Ultimate Reroot Template™
Great Blog !
Btw, what's that "edge DP" technique ?
"edge DP" stores the dp value of a subtree (if you had done it without thinking about rerooting). Note that any of the endpoints of an edge can be a root, so you need to specify which endpoint is the root.
Here is the idea behind "Edge DP". Consider some edge $$$(u,v)$$$ with
edge_index$$$i$$$ (meaninggraph[u][i]is $$$v$$$).Suppose now that we would want to analyze something about this edge. Maybe we want to know what happens if we remove (u,v) from the tree. Or maybe we want to know how many paths with some certain property that pass through (u,v). There are then two natural questions:
Using the reroot template, the answer to 1 is given by
forwardDP[u][i]and the answer to 2 is given byreverseDP[u][i].So not only can the reroot template be used to solve standard reroot problems. The template can also be used to solve "Edge DP" problems, where you are tasked to compute some property of each edge.
See 868E - Policeman and a Tree
more problems https://open.kattis.com/problems/joiningnetwork https://open.kattis.com/problems/fulldepthmorningshow
Thanks for this, very cool. I have taken your template and put in a Python class. Extending that class and overwriting the default_value, combine and finalise methods in line with this blog is all that's required, see here: https://codeforces.com/contest/1324/submission/240262918.
What? Linear solution is easy, just store all prefix/suffix aggregates. Code
The $$$O(n \text{log} (n))$$$ reroot template only ever merge a child into its parent (using the
combinefunction). On the other hand, the $$$O(n)$$$ method of using prefix/suffix merges multiple children into each other in some weird way. This is a fundamental difference that makes the $$$O(n \text{log} (n))$$$ template a lot easier to use, especially on more complicated reroot problems.I feel when the post talks about the faster $$$O(n)$$$ version, it repeatedly uses strong words such as "weird, fundamental, superior" while avoiding any actual comparison, which makes it feel very fishy. You have a weird restriction of merging a child into its parent and it slows up your solution. I think it is unnecessary. Can you elaborate, with sufficient examples, why that is an "unweird" assumption and why the natural order of children is "weird"?
Maybe 219D - Choosing Capital for Treeland is a good example to show my point.
First as a warm up, suppose we want to solve the fixed root version of the problem: "If the capital is at node $$$1$$$, how many roads would have to be inverted?". The solution to this problem is simply
To solve the full problem, we can essentially plug this code into the $$$O(n \text{log} (n))$$$ reroot template.
240150642
On the other hand, if you want to solve 219D - Choosing Capital for Treeland in $$$O(n)$$$ using prefix/suffix, then I don't directly see how to do it. I'm sure it is still possible. But it is definitely not as easy as solving the fixed root version of the problem.
Come on, with my $$$O(n)$$$ template it's just "implement a+b": Code
I don't think you've understood the $$$O(n)$$$ solution.
I mean, yes, you've solved the problem. But from what I can gather, you had to make rather messy changes to your "template".
and
Would you agree with me that what you have done here is more complicated than solving the fixed root version of the problem?
I did not changed them from my github template...
Here is an O(n) implementation of 219D using prefix/suffix. The problem-specific details are in solve (for I/O) and the ART struct.
219D
This method requires only two functions to implement — this is only advantage, less thinking. In most problems with additional $$$O(logn)$$$ factor solution still fits into TL.
If I were (1) cautious and (2) able to give up some functionality, I can remove the
E()function, and mergetake_vertexandup_rootfunction into one. I don't think we gain too much from such "less thinking".Cool, but I can't see how they can be merged
Just like
to
which is probably what the author is doing, I suppose.
I think very last
take_vertexfor each vertex is still required.OR
take_vertex_and_up_rootmust maintain "nothing" values fromeYeah, there should be
e = NILoption if you insist on the merged functionSo after some sleeping I can definitely say that this looks like trash against just one link operation
maybe then stop sleeping and solve more problem to figure why not
Lack of sleep will make me feel this method more convenient? Genius.
why the line 45 on your library is
vector<elem> pref(sz(gph[z]) + 1);instead ofvector<elem> pref(sz(gph[z]) + 1, E());I guess I thought
pref[0] = up_root(rev_dp[z], pae[z]);supplies the base case so it's unnecessary. But it looks sketchy whenzis a root... I will just change tovector<elem> pref(sz(gph[z]) + 1, E());.I try to solve this using your library, but it could not pass the example. After some debugging, i found that line...
Anyway, your template is amazing!
BTW, could you show how to solve this problem in best(your) way, i solve it using your code again, but with struggling work...
Here you go. Note that the inner function (last 10~15 lines of
solve) is changed so that it can read the final answer more conveniently. I did not, but you may want to change some design specifics (e.g. adding edge/vertex parameter totake_vertex,up_rootor likewise). I generally don't care too much about specific design choices and it's really up to you to figure what could be a way to enhance this.thanks, learn a lot!
Your code is much simpler than mine.
how could i did not notice that it was two-diameter's combine.
can someone paste this working code into a pastebin, i trying to learn but the link wont work.
sorry I fixed.
Here is how I would solve 104008G - Group Homework 240418335
Thanks for your sharing.
Your blog (as well as the discussions) really helps me, i am just the one always struggling in rerooting...
One more thing, your solution is not Ultimate: It assumes that the aggregate of any set of subproblems are always small. We can always create a tree DP problem that violates this property and also be solvable. The trick is we just throw in some data structure problems, e.g:
This makes less sense as a CP problem, but nonetheless, they have a near-linear time solution. So you do make some compromises here.
I guess the possible extra compromise is that I assume associativity, but I don't think that's a big problem, since:
Btw I always assumed you can forget about rerooting and do memoized edge dp but the problem in edge dp is that if your state is $$$dp[edge]$$$ and inside you're iterating over $$$adj[node]$$$ that can go up to $$$O(N^2)$$$ in the case of star trees.
My solution for the above issue would be to calculate that you can calculate the solutions of edges without doing the normal calculation by doing some inc-exec tricks for example :
I tried this once or twice and it worked but I find it very difficult to do from scratch most of the times and it does have it's own fuck ups dpending on the problem
I'm not trying to do this all day, but I just found another reason why your take is not so superior, and this is the most nontrivial and funny one.
What this code does is a special case of rake-compress paradigm, which is important when you want to use Top trees. The implementation of top tree I know requires three kind of subtree aggregation method, and they exactly correspond to what I do:
mergefunctionup_rootfunctiontake_vertexfunctionNote that the compress node isn't exactly the same as what
up_rootdoes. Whileup_rootis incremental (add a single edge in the back), compress node merges two long paths. This makes the implementation in top tree harder, because usually you have to store information assuming both side of endpoint being a root, kinda similar as why seg-tree version of maximum subsegment is harder than the linear one. On the other hand, for the rake node it is exactly equivalent to themergefunction, and the implementation here is usually straightforward because this is similar to how most tree DP works.So if you are somehow not used to this way of implementation and having trouble adapting it, maybe now is high time, before chill ds enjoyers copy more top trees to cheese Div1F.
There is a cf discord server?
shash4321 and I created this template for rerooting: https://github.com/kelly-dance/mactl/blob/main/content/various/AllRoots.h
Our approach uses prefixes/suffixes as discussed by ko_osaga here https://codeforces.com/blog/entry/124286#comment-1103422.
We assume commutativity and associativity of our merge operation, but do not require reversibility.
Utilizing the template only requires modifying the
ARTstruct. Or occasionally adding.promote(i,-1)on line 65.operator+should merge aggregates.promotetakes the aggregate for some child nodes and upgrades it to be the aggregate representing the parent.I just finished solving all the problems linked in this post using this template. It was a great collection, thanks for putting this together!
Here are a couple problems that shash4321, asiad, and I have encountered that have not yet been linked by other commenters:
https://codeforces.com/contest/1825/problem/D1 (210638113)
https://cses.fi/problemset/task/1132 (https://cses.fi/paste/cc3cef8f5f02c90f7c0235/)
https://cses.fi/problemset/task/1133 (https://cses.fi/paste/883468c70b26846c5d50b1/)
https://atcoder.jp/contests/dp/tasks/dp_v (https://atcoder.jp/contests/dp/submissions/49030122) (This problem is what inspired shash4321 to make the template!)
https://codeforces.com/problemset/problem/1796/E (240178306)
https://codeforces.com/contest/1794/problem/E (shash4321's solution: 196311155)
https://codeforces.com/gym/104665/problem/H (227755196)
https://open.kattis.com/problems/nuremberg (https://gist.github.com/kelly-dance/9a7b320213d2523e8585c1a4bf205f90)
Note that some of my linked submissions utilize older versions of our template.
One of the main downsides of trying to use a catch all template for these problems is memory usage. We haven't figured out how to pass this problem with our template: https://www.acmicpc.net/problem/14875
Modified the template to use less memory, the implementation can be seen here: 240644685
Auto comment: topic has been updated by pajenegod (previous revision, new revision, compare).
Auto comment: topic has been updated by pajenegod (previous revision, new revision, compare).
can anyone help me with problem 1881F- Minimum maximum distance with rerooting ?. I think that when reroot vertex u with its parent, we should consider the maximum dp of others children of parent, but this seems give me a TLE.
https://codeforces.com/contest/1881/submission/261603990
here is my sol