K-th ancestor of a node & LCA of two nodes in a tree using binary search

#	User	Rating
1	tourist	3880
2	jiangly	3669
3	ecnerwala	3654
4	Benq	3627
5	orzdevinwang	3612
6	Geothermal	3569
6	cnnfls_csy	3569
8	jqdai0815	3532
9	Radewoosh	3522
10	gyh20	3447

#	User	Contrib.
1	awoo	161
2	maomao90	160
3	adamant	156
4	maroonrk	153
5	atcoder_official	149
6	-is-this-fft-	148
6	SecondThread	148
8	Petr	147
9	nor	144
9	cry	144

Hi everyone!

Recently, I came across two CSES problems, Company Queries I and Company Queries II. And I had an unusually simpler approach for both of the problems, which doesn't use binary lifting or LCA algorithms, rather it uses binary search on the levels of the tree

Recap

An ancestor of node $$${X}$$$ is node $$${Y}$$$, where node $$${X}$$$ is contained within the sub-tree of node $$${Y}$$$ (downwards)
The LCA (lowest common ancestor) of nodes $$${A}$$$ and $$${B}$$$ is the nearest node which have $$${A}$$$ and $$${B}$$$ in its sub-tree

Company Queries I

The algorithm described here needs $$$O(N\log N)$$$ for preprocessing the tree, and then $$$O(\log N)$$$ for each query

Here's the step by step algorithm to get the $$$k$$$-th ancestor of a node:

use depth-first search on the tree, and assign each leaf node an arbitrary increasing index (unique for all leaf nodes)
in the dfs function, keep track of the maximum index the current node covers, and store it for every node
use breadth-first search, and assign for each node the level in which it's in. Also for every level, add the nodes contained in that level and sort them by the maximum index they cover
for every query of the form "what is the $$$k$$$-th ancestor of node $$$X$$$" we will get the level in which our answer is in simply as

$$$lvl = level[X] - k$$$

if $$$lvl$$$ is below 1, means it's an invalid level. Otherwise, binary search in that level on the node that contains the maximum index that node $$$X$$$ covers

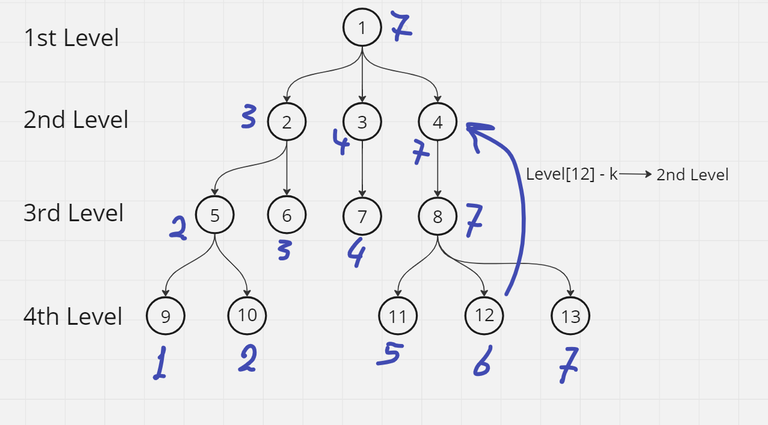
Here is an image to help you visualize how the algorithm works, the number written beside each node is the maximum index it covers in its sub-tree. in this image we query on node $$$12$$$ and $$$k = 2$$$, so we go back to the second level, then binary search on the node that covers the index of node $$$12$$$ which will be node $$$4$$$ in this case

Here's the code for $$$k$$$-th ancestor of a node:

code

#include<bits/stdc++.h>
using namespace std;

const int MXN = 2e5 + 5, INF = 1e9 + 5;
const int MOD = 1e9 + 7;

int n, m;
vector<vector<int>> adj(MXN);
vector<set<pair<int, int>>> levels(MXN);

int level[MXN];
int cnt = 1;
int last[MXN]{};

int dfs(int x = 1){
    if(adj[x].size() == 0){
        last[x] = cnt;
        cnt++;
        return last[x];
    }

    for(int y : adj[x]){
        last[x] = max(last[x], dfs(y));
    }

    return last[x];
}

void solve(){
    cin >> n >> m;
    for(int i = 2; i <= n; i++){
        int x; cin >> x;
        adj[x].push_back(i);
    }

    dfs();

    queue<array<int, 2>> q;
    q.push({1, 1});
    while(q.size()){
        array<int, 2> a = q.front(); q.pop();
        int x = a[0];

        level[x] = a[1];
        levels[a[1]].insert({last[x], x});

        for(int y : adj[x]){
            q.push({y, level[x] + 1});
        }
    }

    while(m--){
        int x, k; cin >> x >> k;

        int lvl = level[x] - k;

        if(lvl < 1){
            cout << "-1\n";
            continue;
        }
        
        cout << levels[lvl].lower_bound({last[x], 0})->second << endl;
    }
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(0);
    cerr.tie(0);

    // freopen("filename.in", "r", stdin);
    // freopen("filename.out", "w", stdout);

    int TC = 1;
    // cin >> TC;
    while(TC--) solve();
    return 0;
}

Company Queries II

The algorithm described here needs $$$O(N\log N)$$$ for preprocessing the tree, and then $$$O(\log^2 N)$$$ for each query

This problem wants us to find $$$LCA(A, B)$$$. This algorithm does mostly as the previous one did, here's what we'll change:

for every node, store the maximum index it covers and also the minimum index it covers
for each query, identify the range of indices they cover as: $$$X$$$ covers from $$$mn1$$$ to $$$mx1$$$ and $$$Y$$$ covers from $$$mn2$$$ to $$$mx2$$$
binary search on all the previous levels, and binary search inside the current searched level on whether there is a node that covers from $$$mn1$$$ to $$$mx2$$$ (covers all the range that $$$X$$$ and $$$Y$$$ covers)
if we find a node that satisfies this condition, save it and search in deeper levels, else, go search up the tree

Here's the code for $$$lca(a, b)$$$:

code

#include<bits/stdc++.h>
using namespace std;

const int MXN = 2e5 + 5, INF = 1e9 + 5;
const int MOD = 1e9 + 7;

int n, m;

vector<vector<int>> adj(MXN);
vector<set<array<int, 3>>> levels(MXN);

int level[MXN];
int cnt = 1;
int last[MXN]{}, start[MXN]{};

pair<int, int> dfs(int x = 1){
    if(adj[x].size() == 0){
        start[x] = last[x] = cnt;
        cnt++;
        return {last[x], last[x]};
    }

    for(int y : adj[x]){
        pair<int, int> p = dfs(y);

        start[x] = min(start[x], p.first);
        last[x] = max(last[x], p.second);
    }

    return {start[x], last[x]};
}

void solve(){
    cin >> n >> m;
    for(int i = 2; i <= n; i++){
        int x; cin >> x;
        adj[x].push_back(i);
    }

    fill(start, start+n, INF);
    dfs();


    queue<pair<int, int>> q;
    q.push({1, 1});
    while(q.size()){
        pair<int, int> p = q.front(); q.pop();
        int x = p.first;
        int current_level = p.second;

        level[x] = current_level;

        levels[current_level].insert({last[x], start[x], x});

        for(int y : adj[x]){
            q.push({y, current_level + 1});
        }
    }

    while(m--){
        int a, b; cin >> a >> b;

        int mx1 = min(last[a], last[b]), mx2 = max(last[a], last[b]);
        int mn1 = min(start[a], start[b]), mn2 = max(start[a], start[b]);

        int lo = 1;
        int hi = min(level[a], level[b]);
        int saved = 1;

        while(lo <= hi){
            int mid = (lo + hi) / 2;

            auto it = levels[mid].lower_bound({mx2, 0, 0});

            if(it == levels[mid].end()){
                hi = mid - 1;
                continue;
            }
            
            int low = it->begin()[1];
            int high = it->begin()[0];
            int ind = it->begin()[2];

            if(low <= mn1 && mx2 <= high){
                lo = mid + 1;
                saved = ind;
            }else hi = mid - 1;
        }

        cout << saved << endl;
    }
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(0);
    cerr.tie(0);

    // freopen("filename.in", "r", stdin);
    // freopen("filename.out", "w", stdout);

    int TC = 1;
    // cin >> TC;
    while(TC--) solve();
    return 0;
}

Conclusion

These algorithms run in time complexities worse than the standard LCA and binary lifting algorithms but just optimized to be accepted as a solution. As we store a tree level's information we can use binary search to construct a simple beginner-friendly solution for these two problems without the kind of complicated LCA and binary lifting algorithms

Youssef_Elwazzan's blog

Recap

Company Queries I

Company Queries II

Conclusion