Problem Link: http://uva.onlinejudge.org/external/120/12003.html
I have solved this problem using sqrt decomposition and treap . In sqrt decomposition per query cost is O(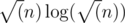 ) and treap is O( log(n)*log(n) ) . Both of my method took ~3.3s and ~4.5s respectively . I want to know if there is any faster method as there seems to be ~1s solution on the statistics.
) and treap is O( log(n)*log(n) ) . Both of my method took ~3.3s and ~4.5s respectively . I want to know if there is any faster method as there seems to be ~1s solution on the statistics.
Thanx :)











Try to think about segment tree where the internal nodes are multisets. The complexity per query is O(log(n)2). Maybe it will be faster. And why the complexity using treap is O(log(log(n))) ?
Sorry , my treap implementation's complexity was written written wrong . I did a binary index tree where each node is a treap . I want to know if there is better complexity , thanx :)
I think you're using sqrt-decomposition in a needlessly inefficient way. You can just update the array after each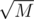 steps; when checking how many integers are ≤ x, you can look at the numbers that changed since the last update (
steps; when checking how many integers are ≤ x, you can look at the numbers that changed since the last update (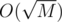 of them) and the answer for the array right after that update.
of them) and the answer for the array right after that update.
Getting that answer is the only difficult part. But the problem's offline, so you can look at the next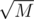 queries, check the x in them, sort them and, using 1 traversal of the sorted array, find out these answers.
queries, check the x in them, sort them and, using 1 traversal of the sorted array, find out these answers.
Note that as only 1 number changes in each query, you can get the sorted array by storing it in a set<> (and updating it in each query).
Time: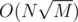 .
.
I've been thinking about your solution, and I don't seem to get it.
What I did to solve it, was to use a simple sqrt decomposition, using blocks with values sorted, and
lower_boundto find out for each block the answer. This should be $$$O(N\log_2 (\sqrt{N}))$$$ for initial build, and then the queries are answered in $$$O(M\sqrt{N}\log_2 (\sqrt{N}))$$$. Using a block size bigger than $$$\sqrt{N}$$$ (1000 instead of 547), I got a very good time, around 0.7 seconds. Also, this is more or less the same I found in every other solutions posted online. Here is my code.But you solution seems to be much faster than this. I understand how you get the $$$O(N\sqrt{M})$$$, but I cannot figure out how to code this "check the x in them, sort them and, using 1 traversal of the sorted array, find out these answers."
Anyway, thank you for your explanation.