Today, when I solved problem C from the Contest #260 (455C - Civilization), I wrote a routine to find the center of each tree before proceeding to the queries and the DSU.
Later, after getting AC, I read other coders' solutions and it seems like finding the centers wasn't necessary for this problem. From what I've seen in the codes, it seems like there's a theorem that states something like the following: If the diameter of a tree is d, there will always be at least one node v such that the farthest node from v is no farther than (d + 1) / 2.
Is there such a theorem? I'd be grateful if someone could enlighten me on the matter.











If the longest simple path in tree is A — B, then central node C on this path (any of them, if multiple) is what you need. If there is node D, that is more than (d + 1) / 2 away from C, then one of the paths A — C — D or B — C — D will be longer then diameter.
Yeah, you're right. Thanks.
We know that the center of the tree is in the middle of the path between the two furthest leafs. You can also see that the longest path from the center of the tree to a leaf is
(d + 1)/2. When merging two of these trees it's pretty intuitive that the best way to do so is connecting the centers of each tree. The new diameter will be the max between the diameter of each tree, and a new path that crosses this new edge (between the center of the trees). This new path can have a length of:(d_a + 1)/2 + (d_b + 1)/2 + 1So you don't need to determine the center of the tree, only it's diameter since you don't need to construct the new graph.Hope that it helps ;)
Yeah, I had that other part of optimum merging figured out, I just didn't notice that I didn't need to find the actual center of the tree, just the diameter.
Thanks for your reply.
It's easy to guess that if you find one longest path of length d edges, then such a vertex (centroid, although this name is ambiguous) could be either one of the (at most 2) vertices in the middle of this path. If we pick one (call it c), we can prove what you ask by contradiction.
We know that one end vertex (u) of this path is at least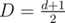 (integer division) far from c and the other (v) at least d - D far. Also, u and v lie in subtrees of different sons of c for d ≥ 2.
(integer division) far from c and the other (v) at least d - D far. Also, u and v lie in subtrees of different sons of c for d ≥ 2.
Let there be a vertex w which is further than D from c. Then, one of paths u - w and v - w must cross c, because if neither did, then u, v would need to be in the same son's subtree; the length of this path is at least D + 1 + (d - D) = d + 1 edges, which is a contradiction — we found a longer path.
Thanks a lot.
Could anyone give some center of tree related problems?