Jacobi's Two Square Theorem: The number of representations of a positive integer as the sum of two squares is equal to four times the difference of the numbers of divisors congruent to 1 and 3 modulo 4.
I find this on Google , but not able to find any proof . I have brute force it and find that this is correct. Can anyone tell me any proof or whether any test case on which this theorem fails. Really needed please help.










Google gives me this on the first page of the results.
Thank you so much
You could google it yourself.
But I still don't see all the four ways of representing 1 as a sum of two squares. 1 = 02 + 12 = 12 + 02. How else?
02 + ( - 1)2 = ( - 1)2 + 02 = 1
Oh, the statement is so ambiguous. Two important facts are omitted: negative numbers' squares are allowed and negative divisors are forbidden. It's a shame :).
for this theorem , We consider both order as well as sign.
I would be thankful if you explain what is going on in this paper.
I'd be glad to do it, but my knowledge of formal power series approaches to zero.
So why you write it as an answer for the question?
Why not to do that? I googled for "Jacobi's Two Square Theorem" and found this article on the first page of the search result.
If the author couldn't understand the proof, he must say that he didn't understand the proof, but not what I've just cited.
BTW, such mathematics-heavy questions should be asked on specialized forums, not here.
There is much more easier proof; let p be a prime in form 4k + 1. Then exists a number x such that x2 = - 1 (p). For example,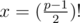 satisfies this condition because of Wilson Theorem.
satisfies this condition because of Wilson Theorem.
Lets consider numbers of type a + bx, where are a, b integers in range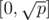 . Obviously there are more than p such numbers, so, by Pigeonhole principle, we can get four numbers a, b, c, d({a, b} ≠ {c, d}) such that a + bx = c + dx (p), so, a - c = x(d - b) (p), then, (a - c)2 = - (b - d)2 (p), so, (a - c)2 + (b - d)2 = 0 (p).
. Obviously there are more than p such numbers, so, by Pigeonhole principle, we can get four numbers a, b, c, d({a, b} ≠ {c, d}) such that a + bx = c + dx (p), so, a - c = x(d - b) (p), then, (a - c)2 = - (b - d)2 (p), so, (a - c)2 + (b - d)2 = 0 (p).
a, b, c, d are in range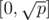 , so (a - c)2 + (b - d)2 obviously is between 0 and 2p. It's divisible on p, so, it is exactly equal to p. Theorem is proved.
, so (a - c)2 + (b - d)2 obviously is between 0 and 2p. It's divisible on p, so, it is exactly equal to p. Theorem is proved.
It is not theorem topicstarter is talking about.
Oh, I so blind:(
But, 5 users found it interesting and even put the pluses, so it wasn't very harmful:)