If n+1 integers a0,a1,a2.....an are given then how can we find efficiently the value of
nC0*a0 -nC1*a1 + nC2*a2 -nC3*a3 + ..... +/- nCn*an (mod 1000000007)
Actually this is the problem of hackerrank.com's SprintIndia qualification round.
n<=10^5 and time limit is 2 sec.
Thanks in advance.. :)











Do you mean the value
modulo some prime? It's just straightforward summation, plus precalculated factorials and their modular inverses, in O(N).
Sorry, I forgot to mention to find the value mod 10^9+7.
How can it be done in O(N)?
For e.g n=100000, we need all these values 100000C0,100000C1,..... 100000C50000.... which is calculated in O(N*N)
If you don't know what a modular inverse is, look it up. Then, you can just use the formula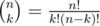 to calculate a binomial coefficient in O(1) by multiplication.
to calculate a binomial coefficient in O(1) by multiplication.
If you use modular inverse, then you must calculate n! * ( k! * (n-k)! ) ^ (MOD-2) How can you do it in O(1) time.
Technically in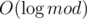 , but I just considered that constant for simplicity. (Usually, it's better to pre-calculate modular inverses in case you need to use them more often, to save time.)
, but I just considered that constant for simplicity. (Usually, it's better to pre-calculate modular inverses in case you need to use them more often, to save time.)
And you can calculate modular inverses to first n integers in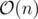 time using this formula:
time using this formula:
So it is really
Could you explain your idea that calculating it in O(N) with details ?
Well, you want calculate modular inverses to first n factorials modulo p = 109 + 7.
So you can calculate modular inverses to 1, 2, ..., n and get all factorial modular inverses in O(n) time.
Modular inverses to 1, 2, ..., n can be calculated with dynamic programming (using above formula, note that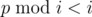 , so if we now inverses to 1, 2, ..., k, we can get inverse to k + 1 in
, so if we now inverses to 1, 2, ..., k, we can get inverse to k + 1 in  ).
).
Proof of formula:
Lets multiply both sides by
We have:
Thank you for your explanation. I got it.