This is an implementation problem, therefore most of the solution fit in the time limit. We can even save the keyboard in 3 strings and make a brute force search for each character to find its position and then print the left/right neighbour.
There are two solutions:
We can make partial sums (sumi = a1 + a2 + ... + ai) and then make a binary search for each query qi to find the result j with the properties sumj - 1 < qi and sumj ≥ qi. This solution has the complexity O(n + m·log(n))
We can precalculate the index of the pile for each worm and then answer for each query in O(1). This solution has the complexity O(n + m)
For each 4 points we want to see if we can rotate them with 90 degrees such that we obtain a square. We can make a backtracking where we rotate each point 0, 1, 2 or 3 times and verify the figure obtained. If it's a square we update the minimal solution. Since we can rotate each point 0, 1, 2 or 3 times, for each regiment we have 44 configurations to check. So the final complexity is about O(n).
We can notate each string as a binary string, instead of red and white flowers. A string of this type is good only if every maximal contigous subsequence of "0" has the length divisible by k. We can make dynamic programming this way : nri = the number of good strings of length i. If the i-th character is "1" then we can have any character before and if the i-th character is "0" we must have another k - 1 "0" characters before, so nri = nri - 1 + nri - k for i ≥ k and nri = 1 for i < k. Then we compute the partial sums (sumi = nr1 + nr2 + ... + nri) and for each query the result will be sumb - suma - 1. This solution has the complexity O(maxVal + t), where maxVal is the maximum value of bi.
We have to find a substring i1, i2, ..., ik such that abs(hij - hij + 1) ≥ D for 1 ≤ j < k. Let's suppose that the values in h are smaller. We can make dynamic programming this way : besti = the maximal length of such a substring ending in the i-th position, besti = max(bestj) + 1 with j < i and hj ≥ D + hi or hj ≤ hi - D. So we can easily search this maximum in a data structure, such as an segment tree or Fenwick tree. But those data structure must have the size of O(maxH) which can be 109. For our constraints we mantain the idea described above, but instead of going at some specific position in the data structure based on a value, we would normalize the values in h and binary search the new index where we should go for an update or a query in the data structure. Therefore, the data structure will have the size O(n). The complexity of this solution is O(n·log(n)).
For each subsequence [L, R] we must find how many queens we have. A value is "queen" only if is the GCD of (sL, sL + 1, ..., sR). Also, we must notice that the GCD of (sL, sL + 1, ..., sR) can be only the minimum value from (sL, sL + 1, ..., sR). So for each query we search in a data structure (a segment tree or a RMQ) the minimum value and the GCD of (sL, sL + 1, ..., sR) and if these two values are equal then we output the answer R - L + 1 - nrValues, where nrValues is the number of values in the subsequence equal to the GCD and the minimum value. The complexity of this solution is O(n·log(n)·log(valMax) + t·log(n)·log(valMax)), where valMax is the maximum value of si.










Why the time complexity of pE is O(n·log(n)·log(n)) other than O(n·log(n))?
+1. Scan the array->O(n) For each element: Do the binary search->O(logn) Get the maximum element from segtree->O(logn)
In total:O(n(logn+logn))=O(nlogn)
I couldn't understand what we're looking with binary search. Can you elaborate?
That's what I thought since a segment tree with dynamic memory is perfect for the problem, but I guess the author's idea is simpler to come up with if you are not familiar with dynamic memory structures.
in problem F nrVaues can be easily calculated in . Let's make pairs {number, occurrence in string}. Then we can do
. Let's make pairs {number, occurrence in string}. Then we can do
nrValue=upper_bound({x,r})-lower_bound({x,l});So we don't even need to find min, only gcd.But the gcd adds the additional log-factor to the complexity, no?
Actually I'm not sure since gcd(a1, a2, ..., an) works in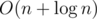 not
not  summary. Maybe you should not multiply but sum logs.
summary. Maybe you should not multiply but sum logs.
Oh, right, I didn't consider that it's not a very tight bound.
i AM not sure
Oh, thank you! Can you also check this, this, this, this and this articles? I would be very grateful!
sarcasm again?
First time to know that upper_bound can make binary search on pairs , Thanks
Can someone please explain why and how does it work in finding number of occurrences of x in the range [l,r]?
Can you please explain question 4
For E as well you don't need extra log factor — use segment tree without normalization.
You can implement segment tree so that it will have a O(N) size, no matter what is the range of the input values.
Could you explain to us this clearly because i can't imagine how to solve this problem ?
i thought about nearly all the solution but got stuck on how to search in a segment tree whose maximum value should be 10^9 ?
In C, it's faster to write (copy-paste) 4 cycles
for(a[0] =0; a[0] < 4; a[0]++)than write a backtrack.Also, my solution to checking if the figure is a square was: try all permutations of vertices and check if they're the vertices of a square in that order on the perimeter. No cases whatsoever and you can be easily sure that it works :D
Also, E: compress A[i], A[i] - D, A[i] + D, take 2 Fenwick trees (for maximum of interval [0, i] and [j, ∞]) and do the standard LIS algorithm.
Can you explain why my C soln failed?
Thanks in advance.
There are 2 main reasons: 1. Overflow (which I had :( ) -> hard to notice. 2. Wrong square checking.
Just because n = 4 doesn't make the complexity of problem C linear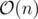 . If the problem was generalized to a regular polygon with n ≤ 20 sides, this wouldn't be possible in linear time. The complexity is exponential
. If the problem was generalized to a regular polygon with n ≤ 20 sides, this wouldn't be possible in linear time. The complexity is exponential 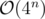 , and in this case n is relatively small.
, and in this case n is relatively small.
Complexity of C problem is O(n*4^4)=O(256n)=O(n). For each quadruple we try every option.Evry point in this quadruple can be in 4 different position,that is 256 combinations.
And what would n be in the case and why was 4 raised to the power of 4?
The complexity of C is O(4pn), where p is the number of moles in one regiment (number of sides of the polygon) and n is the number of regiments (number of queries). For the problem, p = 4 is a constant, so O(4pn) = O(44n) = O(n) because coefficients are not included in big-O notation.
You have mistaken n for the number of moles in one regiment instead.
In problem E, editorial says: "we can easily search this maximum in a data structure, such as an segment tree or Fenwick tree"
How to do this?
Problem E can be solved using implicit segment tree 8119774
Do you know who find the maximum with Fenwick tree?
For example,
http://codeforces.com/contest/474/submission/8115133
Can someone please tell me what's wrong with my solution for problem D. Here's the link > Link
__ When K = 1, it is 2^Length ! __ For any Other K, it works like the Fibonacci sequence !
Where am I going wrong ?
sum[b]-sum[a-1] can be negative
Is it possible to solve pF without segment trees !if yes can someone provide few insights into it !
Sqrt-decomposition also works for given constraints.
Yes, of course. Thanks a ton allllekssssa!
where dp[i][0]: number of ways so that the i length string end with Red and dp[i][1] : number of ways so that the i length string end with white
the above solution is giving WA? can you explain sol
Can you explain how to search maximum in Fenwik tree?
I used treap in this task.
In A, it is not even necessary to store three different arrays, as it is assured you are still hitting the keyboard, and will never hit [q, a, z] when d = R, and never [p, ;, /] when d = L. Therefore just looping through each of the n <= 100 characters on one array containing the entire keyboard works, as well.
On C, it is relatively easy to loop through the small number of vertices and find their rotations, but what criteria are there to calculate if the resulting figure is a square (I did not attempt solving for the reason, but I assumed tilted squares would be included)?
In C, for each possible rotation, I tried all permutations of the 4 points and checked if the lengths were equal, if the angles formed were 90 degrees and if the points were different from each other.
It might be easier to do the following: 1) calculate all 6 possible distances (or distance^2) 2) sort 3) square should have first four and last two distances equal
For the second approach to Problem B, the time complexity seems to be O(sum+m) where sum is the number of all worms. By "precalculate the index of the pile for each worm", I think the author means using an array (of maximum size, 10^6) to remember the pile each worm is in.
http://codeforces.com/contest/474/submission/8112838 This is my solution to 474B It shows wa on pretest 1. The code runs fine on my pc as well as ideone.com Can someone please help?? :(
In some case there is no return in your function solve which will lead to unexcepted answer.Just change the loop condition (from<to) to (from<=to).
Problem : E -> http://codeforces.com/contest/474/submission/8122825
In this, he assumed that his solution sequence will not have any index i,j such that abs(i-j) > 300. Its pure fluke because he tried it before, assuming abs(i-j) <= 800. Both got Accepted. Is there a logic or just weak test cases?
I would also appreciate if someone can give detailed explanation of Problem:E or any link of tutorial because it's a new concept for me.
Thanks.
No logic, just a weak test set. Countertest:
Thanks! Well can you provide some helpful links for similar problems (easier ones to get me started) ?
Problem B i wrote the 1st solution and got time limit :| what's the problem?
Well, it is too slow... :D It is O(m * n). For every x in your solution you may have to look up to n values so it's O((number of x's) * n) = O(m * n). For every x you have to search for the first b[i] >= x with binary search or use lower_bound from stl http://www.cplusplus.com/reference/algorithm/lower_bound/ . Then it will be O(m * log(n)).
someone give proper explanation of which data structure and its implementation for finding max in problem E..
st
@sandyeep can u be more elaborate about the IMPLEMENTATION of st in the problem as the editorialist has not taken effort to explain his approach..
Why this code can pass the test data Your text to link here...
http://codeforces.com/blog/entry/14136#comment-191385 ?
For problem D, could someone further explain how to derive the formula nri = nri - 1 + nri - k for i ≥ k? Thanks!
EDIT: Get it now!
If the i-th position is R, then there could be nri - 1 possibilities, if the i-th position is W, we have to have k Ws, taking the last k positions, therefore nri - k possibilities. Thus nri = nri - 1 + nri - k in total.
For problem D Could you please explain .... why we have to do sumb - suma - 1.?
It's called a cumulative sum trick, you can google it for more info
D: why k=1 is not special??
Check my solution maybe it helps 96383497
Can anybody please explain editorial of problem E-pillars broadly?
Hello please someone here helpmeout in finding mistake in my code of Problem D I am getting wrong answers on some of the outputs[submission:51238549]
Can anyone explain me the problem statement of the problem D.Flowers.
I cannot figure out what is wrong in my solution for 474E Pillars. I have used 2BIT for prefix and suffix max queries. It would be very helpful if someone can find out where the problem is. My submission: https://codeforces.com/contest/474/submission/59685511
Hey guys I was working on problem D and deduced this formula: f(i)=1+(t*(i+1))%m — ((k*t*(t+1))/2)%m; Here t is [i/k]. Idk why but this fails on test case 3. Here f(i) denotes the answer for i'th length. Here is the link to my submission. Please look into this if you can as I saw no comments/solutions using this formula!!!
Hey, the derived formula is wrong as this formula considers only cases where all whites are together ,
i.e. if k=2, it considers only cases like RWWWWR, WWWWRR etc
and not the cases RWWRWW
Can anybody tell me what is wrong in my code for problem D. Here is the link to my solution 80443947
You can refer this
Can Anyone please explain question 4
I found that the solution in the editorial is somewhat hard to understand for some people. Hence posting my different and detailed alternative explanation for problem D.
Consider $$$dpr[i]$$$ be the count of sequences ending with red flower and of size $$$i$$$
Consider $$$dpw[i]$$$ be the count of sequences ending with white flower and of size $$$i$$$
to get a sequence of size $$$i$$$ ending with red flower, we can append an 'R' at any sequence of size $$$i-1$$$
hence $$$dpr[i] = dpw[i-1] + dpr[i-1]$$$
Since we can never use a single 'W', we can only use 'WWW..W'($$$k$$$ times) . To get a sequence of size $$$i$$$ ending with white flower, we append a 'WWW...W' of size $$$k$$$ at any sequence of size $$$i-k$$$.
$$$dpw[i] = dpr[i-k] + dpw[i-k]$$$ .
We may handle $$$i==k$$$ and $$$i<k$$$ seperately.
https://codeforces.com/contest/474/submission/184377287 : Accepted submission using same idea.