Problem A
Fist, consider the case when all the numbers are non-zero. You can take a*c*e grams of sand, turn them into b*c*e grams of lead, and them turn into b*d*e grams of gold, and them turn into b*d*f grams of sand. If b*d*f > a*c*e, you can infinitely increase the amount of sand and consequently the amount of gold. Otherwise, if b*d*f <= a*c*e, it is impossible to get infinitely large amount of gold. The same is true when the fraction (a*c*e)/(b*d*f) has zero numerator only or zero denuminator only. Otherwise there is 0/0, and you have to check cases specially.
I explain, why I make this problem to be problem A.
1. Solution of the problem requires very little knowledge of programming (only "if"), so it was feasible for all participants.
2. Tricky cases really exist, but I hoped that "stronger competitors will ... help newcomers to catch all bugs by their hacks". And so it happened.
Maybe I was wrong: this problem is too complex for A.
A large number of hacks for this problem is a quite foreseen circumstance. I haven't include the special class of tests into the pretests intendently, to make hacking more interesting. In fairness I should note that Artem Rakhov was against this idea. Beause of this task the problem surfaced that Gassa writes about here in Russian: pretests cover some incomplete set of cases and it is not clear in advance what the event "solution passed pretests" means. I think it should be discussed, and strong principles of pretests development should be stated.
Problem B
The problem has greedy solution. Change a digit in the first date to make it as small as possible. At each of the next steps try all one-digit exchanges in the current date and choose one that makes the date not less than the previous one and as small as possible at the same time. If the last year won't exceed 2011 - the answer is found. Otherwise there is no solution.
How to prove that? Consider any correct answer. Clearly, if the first date in it is different from the smallest possible number that can be obtained from the first of given years, your can put the smallest number instead of it. The second date can be exchanged by the smallest possible number not exceeding the first number, etc.Ar a result you obtain a greedy solution that is built by the algorithm described above. If the greedy solution doesn't exist, solution doesn't esist too.
The problem also has a dynamic solution.
Problem C
Check for each segment in the polyline if Harry can catch the snitch in it. Note that since vp ≥ vs, if Harry can catch the snitch at some moment of time, he can catch it at any later moment. He can just follow snitch along its trajectory. So use binary search in each segment.
About problems with EPS that participants got. The problems may be caused by
1) some EPS in the condition: while (leftTime + EPS < rightTime) <do binary search>. The task was to output with a fixed accurancy not only the time, but also the point coordinates. If the difference between the time and the right one is less than EPS, the difference between coordinates may be significantly larger. In such cases you should compare not arguments of a function, but values of the function with EPS. Or the way that I usually follow and that once was not liked by the teacher of numerical methods - to implement some fixed number of iterations of the binary search (say, 60).
2) EPS in comparison of time moments inside the binary search like this:
if (currentTime + addTime > distance / potterSpeed - EPS)
rightTime = currentTime;
else
leftTime = currentTime;
Here it is better to remove EPS at all. Or to put EPS significantly smaller than the required accurancy for printing the point.
(Code fragments are from Egor's solution.)
Thus, there was no crime with severe limitations. Probably for such problems extreme accurancy tests should be in pretests? It is about principles of pretests making again.
UPD. The problem has an analytical solution too. Consider the i-th segment. Let (xi, yi, zi) and (xi + 1, yi + 1, zi + 1) be its ends, and let ti be the time required for the snitch to reach the beginning of the segment. Then at the moment t the snitch will be at the point (x, y, z), x = xi + (xi + 1 - xi)(t - ti) / Ti, y = yi + (yi + 1 - yi)(t - ti) / Ti, z = zi + (zi + 1 - zi)(t - ti) / Ti, Ti is a time necessary for snitch to overcome the segment. To catch the snitch at the point (x, y, z), Harry have to overcome the distance that squared is equal to (x - Px)2 + (y - Py)2 + (z - Pz)2 for the time t. It is possible if (x - Px)2 + (y - Py)2 + (z - Pz)2 ≤ (tvp)2. To find the minimal proper moment t, solve the corresponding quadratic equation.
Problem D
Let Si be a set of all possible assignments of the first i students to the houses, that is a set of tuples (a1, a2, a3, a4), where a1 is a number of students sent to Gryffindor, a2 - to Ravenclaw, etc. It's intuitively clear that these sets will not be large. So you can get Si - 1 from Si in a trivial way, and get finally Sn, and determine the answer from it.
What is a rigorous proof of the algorithm? Let us have a set
S = {(ai1, ai2, ai3, ai4)}i = 1, 2, ..., k. Represent its elements as aij = bj + xij, xij ≥ 0, where bj are maximal possible, i.e. there is i for each j such that xij = 0. Let the tuple (b1, b2, b3, b4) be called the base part of S, and the set {(xi1, xi2, xi3, xi4)}i = 1, 2, ..., k be called the variant part of S.
Initially for S0 both base and variant parts are zeroes. Let us see how base and variant parts change when a current student is added. If a house is fixed for the student, only the base part changes. It increases by 1 at the position corresponding to the house. In particular, it follows that a set with every base part can be obtained (since the string given in the input can contain every combination of symbols G, H, R, S). If the current symbol in the string is '?', it can influence both base and variant parts.
For example, for the string '????' we have:
S0 = {(0 + 0, 0 + 0, 0 + 0, 0 + 0)},
S1 = {(0 + 1, 0 + 0, 0 + 0, 0 + 0), (0 + 0, 0 + 1, 0 + 0, 0 + 0), (0 + 0, 0 + 0, 0 + 1, 0 + 0), (0 + 0, 0 + 0, 0 + 0, 0 + 1)},
S2 = {(0 + 1, 0 + 1, 0 + 0, 0 + 0), (0 + 1, 0 + 0, 0 + 1, 0 + 0), (0 + 1, 0 + 0, 0 + 0, 0 + 1), (0 + 0, 0 + 1, 0 + 1, 0 + 0), (0 + 0, 0 + 1, 0 + 0, 0 + 1), (0 + 0, 0 + 0, 0 + 1, 0 + 1)},
S3 = {(0 + 1, 0 + 1, 0 + 1, 0 + 0), (0 + 1, 0 + 1, 0 + 0, 0 + 1), (0 + 1, 0 + 0, 0 + 1, 0 + 1), (0 + 0, 0 + 1, 0 + 1, 0 + 1)},
S4 = {(1 + 0, 1 + 0, 1 + 0, 1 + 0)}.
Let us investigate the question of what species a variant part may have. It can be analyzed independently from a base one, taking into account that a base part can be any. Consider a directed graph with vertices corresponding to variant parts and with edges determined by the existence of
at least one base part that let go from one variant part to another. We are interested only in vertices reachable from {(0, 0, 0, 0)}.
Proposition. For all the vertices reachable from zero the following properties hold
(1) xij ≤ 2,
(2) k ≤ 13.
Let us prove that all the vertices not having the properties (1) and (2) are unreachable from zero. Consider a variant part with the property (1). To get all edges going from it you have to try all possible base parts. Note that base parts, that consist of the numbers 0, 1, 2, 3 and contain at lest one 0, are enough. Indeed, base part influence which elements are minimal, and 1 will be added to them. A base part can be always normed to contain at least one 0. If a base part contains numbers greater than 3, then the corresponding positions will never be minimal (since 4+0 > 0+2) and they can be changed equivalently by 3 (3+0 > 0+2).
Unfortunately, my attempts to deal with cases by hand were unsuccessful, so I wrote the program that traverse the described graph. Starting from 0, it builds edges trying only "small" base parts described in the previous paragraph. As a result, the program obtains all the reachable variant parts (there is a little more than 1000 of them) and check (1) and (2) for them. In addition, the program helps to construct a test with
k = 13.
The problem was supposed to be a problem on intuition. Participants have another solution passed. Their solution generate all permutations and distribute students greedily with respect to each permutation.
This solution was a complete surprise for me. Unfortunately, it is wrong. Test 66 against it was added. Of course, submissions accepted during the round won't be rejudged. If such a solution be expected, most likely I wouldn't give such a task. In terms of intuition this solution is not better and not worse than mine. I hope you will not judge me strictly: it is a beautiful problem, and it was interesting to see how it would be solved.
Problem E
Consider a graph with floors as vertices and staircases as edges. It is clear that Harry can visit the whole connected component in which he is currently located.
Every edge can be used to reach a new vertex for not more than two times. If a connected component contains n vertices and m edges, only n - 1 edges are used to reach a new vertex during its traversal. The remaining m - n + 1 edges are not used to reach a new vertex in their initial placement. So they will be used to reach a new vertex not more than once.
So using edges of only one connected component you can reach no more than n - m + 1 new vertices. Totally there are not more than 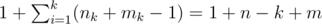 reachable vertices. If m < k - 1, it is impossible to visit all the vertices.
reachable vertices. If m < k - 1, it is impossible to visit all the vertices.
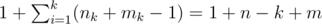 reachable vertices. If m < k - 1, it is impossible to visit all the vertices.
reachable vertices. If m < k - 1, it is impossible to visit all the vertices. We show that otherwise (m >= k - 1), if the degree of the vertex 0 is different from zero, it is possible to visit all the vertices. In other words, there is such a traversal that every edge can be moved. Use depth-first search for the current component. If a current edge goes to an already visited vertex, move it to a new component and traverse it recursively. If a current edge goes to a new vertex, after you visit this vertex and go back, you also can move this edge to a new component. As a result each edge can be moved and used again, if you reach all the components. If a component contains at least one edge, you can go from it to the next one. First visit components with edges, and you will visit them all and by the inequality (m >= k - 1) there are enough edges to visit all the isolated vertices.
If the degree of the vertex 1 is zero, you can not start a traversal before you move some edge to it. After that you can go by this edge and remove it with the vertex 1 from the graph, becase you can not use this edge once more. If the chose edge is a bridge, you get k connected components and m - 1 egdes. If it is not a bridge, you get k - 1 components and m - 1 edges. In the first case the inequality m >= k - 1 turns m >= k. In the second case - m >= k - 1. So if not all the edges are bridges, you should not take a bridge. If they all are bridges, you should disconnect an edge from a vertex of degree >= 2 not to came back to the initial situation with the zero degree of the first vertex. If there is no such vertex, it is easy to check that there is no solution.











If set 2000,I got AC....
You can have a try with {"?HRS"*2500} :)
what might the time complexity of D be?
Here are the 2 interpretations of problem A's solution as I understood them:
64128016
64128379