Hi everyone!
This time I would like to write about the Aho-Corasick algorithm. This structure is very well documented and many of you may already know it. However, I still would try to describe some of the applications that are not so well known.
This algorithm was proposed by Alfred Aho and Margaret Corasick. Its is optimal string pattern matching algorithm. e.g. given the string set {"a", "abba", "acb"} and given text, say, "abacabba". With Aho-Corasick algorithm we can for each string from the set say whether it occurs in the text and, for example, indicate the first occurrence of a string in the text in 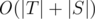 , where |T| is the total length of the text, and |S| is the total length of the pattern. But in fact it is a drop in the ocean compared to what this algorithm allows.
, where |T| is the total length of the text, and |S| is the total length of the pattern. But in fact it is a drop in the ocean compared to what this algorithm allows.
To understand how all this should be done let's turn to the prefix-function and KMP. Let me remind you, the prefix function is called array π[i] = max(k): s[0..k) = s(i - k..i], ie, π[i] is the length of the longest own suffix that matches the prefix of the substring [0..i]. Consider the simplest algorithm to obtain it. Suppose we have counted all the π values on the interval from 0 to i - 1. In this case, we can repeatedly "jump" to positions π[i - 1], π[π[i - 1] - 1], π[π[π[i - 1] - 1] - 1]... and so on. Let the moment after a series of jumps, we are in a position of t. If s[t + 1] = s[i] and t is maximum possible, then π[i] = t + 1. If we will count the π as described above, we will get it in  .
.
Now, let's build automaton that will allow us to know what is the length of the longest suffix of some text T which is also the prefix of string S and in addition add characters to the end of the text, quickly recounting this information. So, let's "feed" the automaton with text, ie, add characters to it one by one. If we can make transition now, then all is OK. Otherwise, we go through suffix link until we find the desired transition and continue. Let's say suffix link is a pointer to the state corresponding to the longest own suffix of the current state. It is easy to see that suffix links in such automatons is the same as π from KMP. So now for given string S we can answer the queries whether it is a substring of text T.
Finally, let us return to the general string patterns matching. Firstly may seem that this is just the beginning of a long and tedious description of the algorithm, but in fact the algorithm has already been described, and if you understand everything stated above, you'll understand what I write now.
So let's generalize automaton obtained earlier (let's call it a prefix automaton) Uniting our pattern set in trie. Now let's turn it into automaton — at each vertex of trie will be stored suffix link to the state corresponding to the largest suffix of the path to the given vertex, which is present in the trie. You can see that it is absolutely the same way as it is done in the prefix automaton. It remains only to learn how to obtain these links.
I suggest doing it this way: run a breadth-first search from the root. Then we "push" suffix links to all its descendants in trie with the same principle, as it's done in the prefix automaton. This solution is appropriate because if we are in the vertex v in a bfs, we already counted the answer for all vertices whose height is less than one for v, and it is exactly requirement we used in KMP. There are also some other methods, as "lazy" dynamics, they can be seen, for example, at e-maxx.ru.
Basic implementation: http://ideone.com/J1XjX6
Alternative one: http://ideone.com/0cMjZJ
You can easily see the KMP in the push_links().
Recommended problems:
- UVA — I love strings!!
- Timus 1269 — Obscene Words Filter
- Timus 1158 — Censored!
- MIPT El Judge 014 — War-cry
- SPOJ — Morse
Later, I would like to tell about some of the more advanced tricks with this structure, as well as an about interesting related structure. So stay tuned :)











Hello, how would you write the matching function for the structure? I tried to do it in this way: The first thing is to pass for every node on the trie and when the node is an end of word i do something with it, but i still have to go to its kmp links because it may have some other matching.
I have been trying: TIMUS-1269 Getting Memory Limit Exceeded on test #7. What is the workaround for this?
It's been a really long time but have you solved it ?
It may be too late, but I just divided all obscene word into two parts. Then I run Axo-Corasick algorithm separately by building a trie for each part again. It has already discussed on discussion of problem.
SPOJ — Morseকেন
Morseভাই?What does the array term[] in your code do here ? What does this array store here?
163E - e-Government
is also a aho problem
SWERC16 E — Password
:)
tnx
nice :)
another problem
*you need to have a lightoj account to see the problem.
Check this list
Is there any problem like : "Find all strings from a given set in a text (or count the number of times each string from a list appears in a text)" ? I try to find one to text my code ...
Thanks in advanced!
Kattis String Multimatching
Thanks so much!!
Try this problem
Try this problem too:Codechef Twostr
please correct me if i am wrong — we are trying to make failure links for the nodes just like LPS array of KMP..
also — how can i solve https://cses.fi/problemset/task/1731 using the same algorithm?