Hi codeforces community.
I thought there is no good 2-SAT tutorial in the internet, so I decided to write one.
2-SAT is a special case of boolean satisfiability.

Good question! Boolean satisfiability or just SAT determines whether we can give values (TRUE or FALSE only) to each boolean variable in such a way that the value of the formula become TRUE or not. If we can do so, we call formula satisfiable, otherwise we call it unsatisfiable. Look at the example below:
f = A ∧ ¬B, is satisfiable, cause A = TRUE and B = FALSE makes it TRUE.
but g = A ∧ ¬A, is unsatisfiable, look at this table:
| A | ¬A | A ∧ ¬A |
| TRUE | FALSE | FALSE |
| FALSE | TRUE | FALSE |
As you can see g is unsatisfiable cause whatever values of its boolean variables are, g is FALSE.
Note: ¬ in ¬X is boolean not operation. ∧ in X ∧ Y is boolean and operation and finally ∨ in X ∨ Y is boolean or operation.
SAT is a NP-Complete problem, though we can solve 1-SAT and 2-SAT problems in a polynomial time.
1-SAT
Note: This doesn't really exist, I define it cause it help understanding 2-SAT.
Consider f = x1 ∧ x2 ∧ ... ∧ xn.
Problem: Is f satisfiable?
Solution: Well 1-SAT is an easy problem, if there aren't both of xi and ¬xi in f, then f is satisfiable, otherwise it's not.
2-SAT
Consider f = (x1 ∨ y1) ∧ (x2 ∨ y2) ∧ ... ∧ (xn ∨ yn).
Problem: Is f satisfiable?
But how to solve this problem? xi ∨ yi and 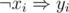 and
and 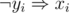 are all equivalent. So we convert each of (xi ∨ yi) s into those two statements.
are all equivalent. So we convert each of (xi ∨ yi) s into those two statements.
Now consider a graph with 2n vertices; For each of (xi ∨ yi) s we add two directed edges
From ¬xi to yi
From ¬yi to xi
f is not satisfiable if both ¬xi and xi are in the same SCC (Strongly Connected Component) (Why?) Checking this can be done with a simple Kosaraju's Algorithm.
Assume that f is satisfiable. Now we want to give values to each variable in order to satisfy f. It can be done with a topological sort of vertices of the graph we made. If ¬xi is after xi in topological sort, xi should be FALSE. It should be TRUE otherwise.
Some problems:
- SPOJ — BUGLIFE
- SPOJ — TORNJEVI
- UVa — Manhattan
- UVa — Wedding
- CF — The Road to Berland is Paved With Good Intentions
- CF — Ring Road 2
- CF — TROY Query
- CEOI — Birthday party — Solution
Pseudo Code
func dfsFirst(vertex v):
marked[v] = true
for each vertex u adjacent to v do:
if not marked[u]:
dfsFirst(u)
stack.push(v)
func dfsSecond(vertex v):
marked[v] = true
for each vertex u adjacent to v do:
if not marked[u]:
dfsSecond(u)
component[v] = counter
for i = 1 to n do:
addEdge(not x[i], y[i])
addEdge(not y[i], x[i])
for i = 1 to n do:
if not marked[x[i]]:
dfsFirst(x[i])
if not marked[y[i]]:
dfsFirst(y[i])
if not marked[not x[i]]:
dfsFirst(not x[i])
if not marked[not y[i]]:
dfsFirst(not y[i])
set all marked values false
counter = 0
flip directions of edges // change v -> u to u -> v
while stack is not empty do:
v = stack.pop
if not marked[v]
counter = counter + 1
dfsSecond(v)
for i = 1 to n do:
if component[x[i]] == component[not x[i]]:
it is unsatisfiable
exit
if component[y[i]] == component[not y[i]]:
it is unsatisfiable
exit
it is satisfiable
exit











How can you topsort if there can be cycles? (between different variables, e.g. x -> y -> x). Or you do it on metagraph?
If x and not x are both in a cycle: unsatisfiable
Else it doesn't matter if x comes first in topsort or y (x and y are in a cycle)
see my solution for 228E
It works because you integrate the topsort in Kosaraju's algorithm. In general a topsort only works on DAG's. If somebody would implement Kosaraju and Topsort seperatly it might fail, maybe you should mention that in the write-up. Otherwise nice tutorial.
If there is a cycle which you can dectect while using toposort, function f is not satisfied.
You're wrong. Consider this example:
f = (x or y) and (not x or not y) is satisfiable with x = TRUE and y = FALSE but corresponding graph has two cycles.
Oh, sorry. Thanks so much :D
You don't need the toposort to check if it's satisfyable (just check if x and ¬x are in the same component). If you need to find some values that satisfy the formula, all that really matters is the topological sorting of the components (not of the actual nodes).
You just need to set a value to a element there (the first component in topological order) and propagate it (according to the logical implication operation and to the fact that if A=True you must set ¬A=False). If you try to propagate to an element that already has a true or false value (and it doesn't clash with the one you're trying to set) you can simply skip it, cause it means you've already propagated from it, so the cycles are not a problem.
Tarjan's algorithm generate the SCCs already in reverse topological order (Kosaraju's generates them in actual topological order if I'm not mistaken), so you don't need anything else apart from the SCC algorithm.
Also, a nice implementation trick (this is from Competitive Programming 3) is to use variable i as node number 2*i and ¬i as (2*i)+1. This way, you can access each one by xoring the other with one. (ex: n(i)^1 will give you n(¬i), and n(¬i)^1 will give you n(i), where n(x) is the node representing variable x).
You might need to be careful with forward propagation. For example, if there's a clause (¬a v ¬a), then the implication a -> ¬a can only be satisfied with a = false.
If you use Kosaraju's algorithm and assign strongly connected components incrementally, that is, the first component found is assigned 1, the second 2, and so on, then you can just compare SCC numbers to determine what is first in topological sort.
Then you assign a = false if SCC[a] < SCC[¬a] and true otherwise.
this ofcourse will happen very rarely, but if you assign 0 and 1's randomly it would mean hours of debugging if something like this comes up.
I have recently created power point for the 2 SAT to explain in competitive programming in my Arabic Channel. Ppt in English.
You may find it useful: https://goo.gl/gBnzKK
Hey in your slides, you have mentioned:
Given (a, b) how to allow only (1, 0) (0, 1) but not (1, 1)
I am unable to think of how to put such a restriction in the algorithm. Can you please elaborate how can we do this?
UPD: I think I have found the answer to it. So here we can replace the
oroperator withxoroperator and then it would be forced to have (1, 0) or (0, 1) but not (1, 1). And the soln toxoris given in this comment: https://codeforces.com/blog/entry/16205?#comment-435812Nice tutorial, Thanks.
I think We can solve 2-sat problems by making the implication graph undirected and using simple dfs to assign components to each vertex.
Please correct me if I am wrong.
This won't work if for example we want to add NAND (not and) clause and for much more clauses. For example look at this problem from HackerRank.
You cannot make the implication graph undirected when there are asymmetrical implications. Consider the following CNF:
Here there is an edge from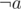 to
to 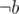 but not vice versa
but not vice versa
Here there is an edge from not a to not b,so the value of not a and not b (also a and b) will be same.so we can keep them in a single component.Thus making an undirected edge will cause no harm.
No. Having an edge from not a to not b doesn't imply their value will be same. Since if a is True, then b can be either True or False.
Thanks,I think i understood it little wrong.
buglife can be solved with simple bfs colouring :P
What kind of data structure would you use to construct the graph? I usually use an adjacency list (vector<vector>) but in this case, the nodes aren't numbered.
You can use the same ds. And number the nodes like x: 2i and !x: 2i + 1 this way you can easily change x to !x and vice versa by “xor”ing with 1.
What to do if you are asked to solve (x1 xor x2) and (x2 xor x3) and .....so on.
Replace
(x1 xor x2)with(x1 or x2) and (not x1 or not x2)and then do 2-satWhat is the idea of the problem? SPOJ-TORNJEVI
Is Kosaraju preferable over Tarjan + explicit toposort for 2-SAT? If so, why?
I thought Tarjan is more well-known than Kosaraju and has a better constant factor.
Using Kosaraju's algorithm, cycle numbers assigned to different SCCs are topologically sorted in the condensation graph. In Tarjan's algorithm, you get SCCs but you have to create the condensation graph and then separately perform topological sort on it.
I learned it when I was solving this question: Question
Kosaraju implementation is easier than Tarjan but the question can be solved using any of them.
Thanks for your good blog. Also there is good 2_SAT Tutorial on Cp_algorithm: https://cp-algorithms.com/graph/2SAT.html :)