534A - Exam
Is easy to see that k = n with n ≥ 4. There are many algorithms that can be used to build a correct sequence of length n with n ≥ 4. For example, students can be seated from left to right with the first to seat students with odd numbers in decreasing order starting with largest odd number. Then similary to seat students with even numbers. In this sequence the absolute difference between two adjacent odd (or even) numbers equal to 2. And the difference between odd and even numbers greater or equal 3 (because n ≥ 4).
Cases n = 1, n = 2, n = 3 are considered separately. Solution complexity — O(n).
Jury's solution: 10691992
534B - Covered Path
It can be easily proved that every second i (0 ≤ i ≤ t - 1) the maximum possible speed is 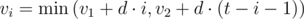 . You can iterate through i from 0 to t - 1 and the values of vi.
. You can iterate through i from 0 to t - 1 and the values of vi.
Solution complexity — O(t).
Also you can use next fact. If current speed equal to u and left t seconds then there is a way to get v2 speed at the end only if |u - v2| ≤ t·d. Consider this criteria, one can simply try to change speed to maximum possible (from u + d down to u - d), choosing first giving a way to reach the end of the path.
Jury's solutions: 10692136 и 10692160
534C - Polycarpus' Dice
Solution uses next fact. With k dice d1, d2, ..., dk you can dial any sum from k to 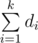 . This is easily explained by the fact that if there is a way to get the amount of s > k, then there is a way to dial the sum equal s - 1, which is obtained by decreasing the value of one die by one.
. This is easily explained by the fact that if there is a way to get the amount of s > k, then there is a way to dial the sum equal s - 1, which is obtained by decreasing the value of one die by one.
Let's denote sum of all n dice as 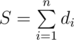 . Fix the dice di (value on it denote as x (1 ≤ x ≤ di). Using the other dice we can select s (n - 1 ≤ s ≤ S - di). We know that average value s + x = A, and n - 1 ≤ A - x ≤ S - di, giving A - (n - 1) ≥ x ≥ A - (S - di).
. Fix the dice di (value on it denote as x (1 ≤ x ≤ di). Using the other dice we can select s (n - 1 ≤ s ≤ S - di). We know that average value s + x = A, and n - 1 ≤ A - x ≤ S - di, giving A - (n - 1) ≥ x ≥ A - (S - di).
Using facts described above, for every dice one can calculate a possible values segment, giving the answer for the count of impossible values of that dice. Solution asymptotic — O(n).
Jury's solution: 10692192
534D - Handshakes
From here we will not consider resulting permutation but correct handshakes sequence (rearranged given sequence). Formally, the sequence of handshakes count ai is correct if and only if ai + 1 ≤ ai + 1 and ai + 1 ≡ ai + 1 ± od{m} and a1 = 0. To form correct sequence, we can use following greedy algorithm.
First, place 0 as the first number. Next, for every following number ai + 1 we will select maximum possible number from numbers left, matching above constraints (in simple case it will be ai + 1, otherwise we will check if ai - 2 left, e.t.c).
The solution may divide given sequence into three parts (depending on modulo by 30), and using, for example, data structure ''set'', quickly find the next number to place into resulting sequence. Such solution will work in  . There is also possible to get O(n) asymptotics using path compression technique.
. There is also possible to get O(n) asymptotics using path compression technique.
Jury's solution: 10692252
534E - Berland Local Positioning System
Suppose that the bus started his way from the stop with number 1 and modulate its way during m stops. For every stop we will calculate how many times this stop was visited by the bus at that way. Check if that counts match counts in the input and update the answer if needed. Then we will try to move the start stop to stop with number 2. It's easy to see that the last visited stop (as long as bus must visit m stops) will move to the next stop. So we need to modulate bus way to another one stop from first stop and from last stop to change the starting stop to another (it makes maximum of four counts to be updated). It could be done in O(1) time.
This way we need to move starting stop to every variant (its count is equal to 2n - 2) and for every variant update the answer if needed. Average solution works in O(n) time.
Jury's solution: 10705354
534F - Simplified Nonogram
This task has several solution algorithms.
One of them could be described next way. Let's divide n × m field into two parts with almost same number of columns (it will be n × k and n × (m - k)). Let's solve the puzzle for every part of the field with brute-force algorithm (considering column constraints on number of blocks) with memorization (we do not need same solutions with same number of blocks in rows). Then we will use meet-in-the-middle approach to match some left part with right part to match constraints on n × m field.
Another solution could be profile dynamic programming, where the profile is the number of blocks in the row.
Jury's solution uses both ideas: 10705343











The submission links for E and F don't work. Probably because you submitted them as a contest manager?
Fixed, sorry for that.
Yernat Bekzat is !!!
For D, I think many contestants have better (more elegant) solutions than the Jury's solution.
My solution for E is to simulate the following cases
Special handling for K 2K 2K .. 2K K: check if all distances are equal. If yes it can be uniquely determined. It not, output -1.
Yeah D looks a little like an overkill to me...
Thanks for your E explanation, in the middle of the contest I thought it could be reduced to fewer cases, what do you think?
Can someone explain D to me? I tried a lot and read all the comments on the announcement blog post as well but could not understand how to solve it.
I will try my best, take the example case 3:
4 0 2 1 1
Let us regroup the input based on the amount of preconditions every person has (0 2 1 1) -> (1), (3 4), (2), the numbers you see now are the indexes (starting with 1), not the preconditions.
All the problem is based on, when could I regroup 3 people to conform a team? Does it matters which guys will conform it?
Well, the second question is easier, it doesn't matter which guys (who are already in the room) team up together. For the other question, you can build a team as soon as a person with the highest precondition enters the room... Why? Because there is no other way to accept lower precondition people to enter, unless of course you kick out some guy, but then again, that's not possible, the only thing you can do to reduce the max level, is to group 3 people.
Take a look at this http://codeforces.com/contest/534/submission/10685298 it follows the same idea here, hope code is clearer than my explanation.
Thanks for the explaination. I saw your submission earlier as well but could not get why the dfs works.
Which I did during competition was to draw the graph, then I noticed there were some vertices where I got stuck, and I could not move forward (keep letting people into the room) if I didn't get to lower vertices.
That's why I am moving in a "level-3" fashion whenever I get stuck, this means I need to build a team, so I can progress with the rest of the guys which are not still on the room.
I have a question about problem D. Many solutions and even editorial solution are using modular calculation, which means handshakes can be dropped more than 3 at one time. (your submission also makes it possible to jump from 100 to 1 etc.) But the description says "Different teams could start writing contest at different times." and what I understood was only one team can be created at one time thus the choice between -2(-3+1, creation of team and entering) and +1. Am I misunderstanding it?:(
Handshakes can go to MAX (where MAX is the total of people) and return to 0 if necessary, then again notice that we are discarding the students with the highest preconditions first.
MAX/3 teams could be created at the same time as I understand, I mean, there is no restriction about how many teams can be formed between a pair of students entering the room.
"Different teams could start writing contest at different times." It still seems somewhat ambiguous to me.. What does this statement mean then? Confused...:(
It means to me that [0, N/3] teams, where N is the amount of people in the room, can be created at ANY time. The redaction sometimes is not the best, but I guess that is the message.
Assume that at the end of the day there were 5 teams, well, those teams could have been formed (and started participating) at different times... is that better?
I thought it meant that x≠y → t_x≠t_y. where x,y are team number and t_x is the time the team created. I think I totally misunderstood it. I got the idea of yours! Thanks for kind explanation.
Looking at the official solution for F, I see it uses meet in the middle.
I was looking at that solution earlier (I also solved that way), and it seems it can solve the problem for m ≤ 30 or even m ≤ 40 since each half can be solved fast enough (lots of accepted solutions did this problem m ≤ 20 without meet in the middle) and the combination is of the same complexity.
So, I was curious why you decided to make the constraints so small. Did you want to allow doing it without meet in the middle?
I don't understand my mistake pls check for me :((
I did not understand E. Could someone explain it? Thanks.
Suppose n=6, m=4. We have to find the answer in the series:
[ 1 ( 2 3 4 ] 5 ) 6 5 4 3 2 1 2 3
First check the first 4(=m) numbers. When we push forward, we don't have to check all of the four numbers again but only two numbers: 1(which should be erased) and 5(which should be added). Update the distance by decreasing by dist(1~2) and increasing by dist(4~5). Update the count by decreasing # of 1, increasing # of 5 (by one each). How do we check the match? We know the update of the count only happens in 2 numbers. Other numbers remain. We maintain the difference count of each numbers, counting how many numbers have different count from the given pattern. That different count is 0 means the match.
Got it. Thank you :)
For the problem F, i didn't understand what is meant by 'we do not need same solutions with same number of blocks in rows' Can anyone explain it to me?
Can someone explain how dp is implemented in problem F ? Thanks in advance!!
Editorial should have detailed explanation.I can't understand problem F.
codeforces editorial's are like hint to the problem.We don't need hint we need explanation.
Could some one please explain why this dp approach is wrong for problem B.
note : rep(a,b) means for(int i = 0 ;i<b;++i)
rep(i,200){ rep(j,200){ dp[i][j] = -INF; } } //memset(dp,-100000000,sizeof(dp)); dp[0][v1] = 0; for(int i = 1;i<=t;++i){ for(int j = 0;j<=110;++j){ for(int l = -d;l<=d;++l){ if((j-l) >= 0 && (j-l)<=110){ if(dp[i-1][j-l] != -INF) dp[i][j] = max(dp[i][j],dp[i-1][j-l] + (j-l)); } } } } cout<<(dp[t-1][v2]+v2)<<endl;don't understand what you mean