As usual, a challenge comes with every problem. I tried not to repeat the mistakes of my previous editorials and made sure that all challenges have a solution =) (except for the italics parts that are open questions, at least for me). Go ahead and discuss them in the comments! General questions about problems and clarification requests are welcomed too.
UPD: I added codes of my solutions for all the problems. I didn't try to make them readable, but I believe most part of them should be clear. Feel free to ask questions.
Let me first clarify the statement (I really wish I didn't have to do that but it seems many participants had trouble with the correct understanding). You had to erase exactly one substring from the given string so that the rest part would form the word CODEFORCES. The (somewhat vague) wording some substring in the English translation may be the case many people thought that many substrings can be erased; still, it is beyond my understanding how to interpret that as 'more than one substring'. Anyway, I'm sorry for the inconvenience.
Right, back to the problem. The most straightforward approach is to try over all substrings (i.e. all starting and ending positions) to erase them and check if the rest is the wanted word. When doing this, you have to be careful not to forget any corner cases, such as: erase few first letters, erase few last letters, erase a single letter, and so on. A popular question was if an empty substring may be erased or not. While it is not clarified explicitly in the statement, the question is irrelevant to the solution, for it is guaranteed in the statement that the initial string is not CODEFORCES, so erasing nothing will not make us happy. From the technical point of view, you could erase a substring from the string using standard functions like substr in C++ or similar, or do some bare-hands work and perform conditional iterating over all symbols. Depending on the implementation, this would be either O(n2) or O(n3) solution; both of these fit nicely.
One way of solving this in linear time is to compute the longest common prefix and suffix for the given string and the string CODEFORCES. If their total length is at least 10 (the length of CODEFORCES), it is possible to leave only some parts of the common prefix and suffix, thus the rest part (being a substring, of course) may be removed for good. If the total length is less than 10, no such way exists. This is clearly O(n) solution (rather O(n) for reading the input, and O(|t|) for comparisons where t is CODEFORCES in our case).
Sample solution: 10973831
Challenge (easy). A somewhat traditional question: how many (modulo some prime number) large Latin letter strings of length n have the property that a (non-empty) substring may be cut out to leave a given string t? Can you solve it in O(n + |t|2) time? In O(n + |t|) time? Maybe even faster? =)
n is up to 106. We may note that there are only 26 + 1 = 65 quasi-binary numbers not exceeding 106, so we could find them all and implement a DP solution that counts the optimal representation for all numbers up to n, or even a brute-force recursive solution (which is not guaranteed to pass, but has a good odds).
Are there more effective solutions? Sure enough. First of all, one can notice that the number of summands in a representation can not be less than d — the largest digit in decimal representation of n. That is true because upon adding a quasi-binary number to any number the largest digit may not increase by more than 1 (easy enough to prove using the standard algorithm for adding numbers). On the other hand, d quasi-binary numbers are always enough. To see that, construct a number m as follows: for every digit of n that is not 0, place 1 in the corresponding digit of m, and for all the other digits place 0. Clearly, m is quasi-binary. If we subtract m from n, all non-zero digits will decrease by 1 (clearly, no carrying will take place), thus the largest digit of n - m will be equal to d - 1. Proceeding this way, we end up with the representation of n as a sum of d quasi-binary numbers. This solution is good for every numeric base, and works in 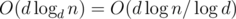 where d is the base.
where d is the base.
Sample solution: 10973842
Challenge (easy). Let us call a number pseudo-binary if its decimal representation contains at most two different digits (e.g., 1, 555, 23, 9099 are pseudo-binary, while 103, 908 and 12345 are not). Represent an integer n as a sum of pseudo-binary numbers; minimize the number of summands. n ≤ 1018.
We want to make the maximum height as large as possible. Consider the part of the chain that was travelled between di and di + 1; we can arrange it in any valid way independently of any other parts of the chain, thus we consider all these parts separately. There also parts before d1 and after dn, but it is fairly easy to analyze them: make them monotonously decreasing (respectively, increasing), as this maximizes the top point.
Without the loss of generality consider di = 0 and di + 1 = t (they may be increased of decreased simultaneously without changing the answer), and hdi = a, hdi + 1 = b. Clearly, in consistent data |a - b| ≤ t, so if this condition fails for a single pair of adjacent entries, we conclude the data is flawed.
If the condition holds, it is fairly easy to construct a valid way to move between the days under the |hi - hi + 1| ≤ 1 condition: increase or decrease the height while it differs from b, than stay on the same height. That does not make the optimal way, but at least we are sure that the data is not inconsistent.
How to construct the optimal arrangement? From the adjacent difference inequality if follows that for any i between 0 and t the inequalities hi ≤ a + i and hi ≤ b + (t - i) hold. Let hi = min(a + i, b + (t - i)) on the [0; t] segment; clearly, every hi accomodates the largest possible value, therefore the value of maximum is also the largest possible. It suffices to show that these hi satisfy the difference condition. Basically, two cases should be considered: if for hi = a + i and hi + 1 = a + i + 1, or hi = b + (t - i) and hi + 1 = b + (t - i - 1), the statement is obvious. Else, hi = a + i but hi < b + (t - i) = hi + 1 + 1, and hi + 1 = b - (t - i - 1) but hi + 1 < a + (i + 1) = hi + 1. Thus, |hi - hi + 1| < 1, and hi = hi + 1.
To find the maximum value of maximum height (I really struggle not to use 'maximum maximum') we may either use ternary search on the h function, or find the point where lines a + i and b + (t - i) intersect and try integer points besides the intersection. If we use this approach analytically, we arrive at the formula (t + a + b) / 2 (try to prove that yourself!).
Sample solution: 10973854
Challenge (medium). Given the same data (that is, a subsequence hdi for a sequence hi), determine how many (modulo a prime number) integer sequences of length n with the property |hi - hi + 1| ≤ 1 agree with the subsequence and have global maximum equal to H? Can you solve the problem in O(n2) time? In  time? Maybe even faster?
time? Maybe even faster?
Instead of trying to find out where the piece may go, let's try to find out where it can not go. Initially mark all the moves as possible; if there is a field (x1, y1) containing a piece, and a field (x2, y2) not containing a piece and not being attacked, clearly a move (x2 - x1, y2 - y1) is not possible. Let us iterate over all pieces and over all non-attacked fields and mark the corresponding moves as impossible.
Suppose we let our piece make all the rest moves (that are not yet marked as impossible), and recreate the position with all the pieces in the same places. If a field was not attacked in the initial position, it will not be attacked in the newly-crafted position: indeed, we have carefully removed all the moves that could take a piece to this field. Thus, the only possible problem with the new position is that some field that was attacked before is not attacked now. But our set of moves is maximal in the sense that adding any other move to it will cause the position to be incorrect. Thus, if the new position doesn't coincide with the initial position, the reconstruction is impossible. Else, we have already obtained a correct set of moves. This solution has complexity of O(n4) for iterating over all pieces and non-attacked fields. No optimizations were needed to make solution this pass.
Sample solution: 10973859
Challenge (medium). Solve the same problem in 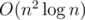 time.
time.
With such large constraints our only hope is the subtree dynamic programming. Let us analyze the situation and how the subtrees are involved.
Denote w(v) the number of leaves in the subtree of v. Suppose that a non-leaf vertex v has children u1, ..., uk, and the numbers to arrange in the leaves are 1, ..., w(v). We are not yet sure how to arrange the numbers but we assume for now that we know everything we need about the children's subtrees.
Okay, what is the maximal number we can achieve if the maximizing player moves first? Clearly, he will choose the subtree optimally for himself, and we are eager to help him. Thus, it makes sense to put all the maximal numbers in a single subtree; indeed, if any of the maximal numbers is not in the subtree where the first player will go, we swap it with some of the not-so-maximal numbers and make the situation even better. If we place w(ui) maximal numbers (that is, w(v) - w(ui) + 1, ..., w(v)) in the subtree of w(ui), we must also arrange them optimally; this task is basically the same as arranging the numbers from 1 to w(ui) in the subtree of w(ui), but now the minimizing player goes first. Introduce the notation 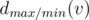 for the maximal possible result if the maximizing/minimizing (depending on the lower index) player starts. From the previous discussion we obtain
for the maximal possible result if the maximizing/minimizing (depending on the lower index) player starts. From the previous discussion we obtain  . Thus, if we know
. Thus, if we know 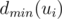 for all children, the value of
for all children, the value of 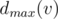 can be determined.
can be determined.
How does the situation change when the minimizing player goes first? Suppose that for each i we assign numbers n1, 1, ..., n1, w(ui) to the leaves of the subtree of ui in some order; the numbers in the subtree of ui will be arranged so that the result is maximal when the maximizing player starts in ui. Suppose that numbers ni, j are sorted by increasing of j for every i; the minimizing player will then choose the subtree ui in such a way that  is minimal. For every arrangement, the minimizing player can guarantee himself the result of at most
is minimal. For every arrangement, the minimizing player can guarantee himself the result of at most 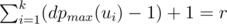 . Indeed, if all the numbers
. Indeed, if all the numbers  are greater than r, all the numbers ni, j for
are greater than r, all the numbers ni, j for 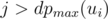 should also be greater than r; but there are
should also be greater than r; but there are  numbers ni, j that should be greater than r, while there are only w(v) - r possible numbers from 1 to w(v) to place; a contradiction (pigeonhole principle). On the other hand, the value of r is easily reachable: place all the numbers less than r as ni, j with
numbers ni, j that should be greater than r, while there are only w(v) - r possible numbers from 1 to w(v) to place; a contradiction (pigeonhole principle). On the other hand, the value of r is easily reachable: place all the numbers less than r as ni, j with 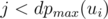 , and r as, say, n1, dpmax(u1); the first player will have to move to u1 to achieve r. Thus,
, and r as, say, n1, dpmax(u1); the first player will have to move to u1 to achieve r. Thus, 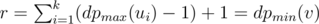 .
.
The previous, rather formal argument can be intuitively restated as follows: suppose we put the numbers from 1 to w(v) in that order to different subtrees of v. Once a subtree of ui contains dpmax(ui) numbers, the minimizing player can go to ui and grab the current result. It follows that we may safely put dpmax(ui) - 1 numbers to the subtree of u(i) for each i, and the next number (exactly r) will be grabbed regardless of what we do (if we do not fail and let the minimizing player grab a smaller number).
That DP scheme makes for an O(n) solution, as processing the k children of each node is done in O(k) (provided their results are already there). As an easy exercise, think about how the optimal arrangement of number in the leaves can be constructed; try to make implementation as simple as possible.
Sample solution: 10973864
Challenge (medium). Suppose that we are given numbers n, a, b, and we want to construct a tree with n leaves such that dpmax(root) = a and dpmin(root) = b. For which numbers n, a, b is this possible? (I'm sure you will like the answer for this one. =)) Can you propose an algorithm that constructs such a tree?
The first approach. For a given k and an element v, how do we count the number of children of v that violate the property? This is basically a range query 'how many numbers in the range are greater than v' (because, evidently, children of any element occupy a subsegment of the array); the answers for every k are exactly the sums of results for queries at all non-leaf vertices. Online data structures for this query type are rather involved; however, we may process the queries offline by decreasing v, with a structure that is able to support an array, change its elements and take sum over a range (e.g., Fenwick tree or segment tree). This can be done as follows: for every element of the initial array store 1 in the same place of the structure array if the element has already been processed, and 0 otherwise. Now, if we sum over the range for the element v, only processed elements will have impact on the sum, and the result of the query will be exactly the number of elements greater than v. After all the queries for v, we put 1 in the corresponding element so that queries for smaller elements would take it into account. That makes for an 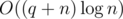 solution. Estimate q: notice that for a given k there are only
solution. Estimate q: notice that for a given k there are only 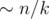 non-leaf vertices, thus the total number of queries will be
non-leaf vertices, thus the total number of queries will be  (harmonic sum estimation). To sum up, this solution works in
(harmonic sum estimation). To sum up, this solution works in  time.
time.
Sample solution (first approach): 10973867
The second approach. Let us index the elements of the array starting from 0. It is easy to check that for a given k the parent of the element av is the element 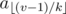 . One can show that there are only
. One can show that there are only  different elements that can be the parent of av for some k. Indeed, if
different elements that can be the parent of av for some k. Indeed, if 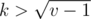 , the index of the parent is less that
, the index of the parent is less that  , and all
, and all 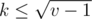 produce no more than
produce no more than  different parents too. Moreover, each possible parent corresponds to a range of values of k. To show that, solve the equality
different parents too. Moreover, each possible parent corresponds to a range of values of k. To show that, solve the equality 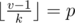 for k. Transform:
for k. Transform: 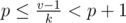 , pk ≤ v - 1 < (p + 1)k,
, pk ≤ v - 1 < (p + 1)k, 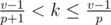 ,
, 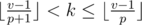 . For every k in the range above the property is either violated or not (that depends only on av and ap); if it's violated we should add 1 to all the answers for k's in the range. That can be done in O(1) offline using delta-encoding (storing differences between adjacent elements in the process and prefix-summing them in the end). There will be only
. For every k in the range above the property is either violated or not (that depends only on av and ap); if it's violated we should add 1 to all the answers for k's in the range. That can be done in O(1) offline using delta-encoding (storing differences between adjacent elements in the process and prefix-summing them in the end). There will be only 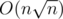 queries to the delta array (as this is the number of different child-parent pairs for all k). This makes for a simple
queries to the delta array (as this is the number of different child-parent pairs for all k). This makes for a simple 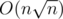 solution which barely uses any heavy algorithmic knowledge at all.
solution which barely uses any heavy algorithmic knowledge at all.
Sample solution (second approach): 10973868
Challenge 1 (medium). Denote ck the minimal number of elements that should be changed (each to a value of your choice) so that the array becomes a valid k-ary heap. Can you find a single ck (for a given k) in  time? Can you find all ck (for 1 ≤ k ≤ n - 1) at once in O(n2) time? Can you do better than these estimates?
time? Can you find all ck (for 1 ≤ k ≤ n - 1) at once in O(n2) time? Can you do better than these estimates?
Challenge 2 (hard). Solve the problem from Challenge 1 if an arbitrary rooted tree with numbers in vertices is given (that is, change the minimal number of elements so that no element is greater than its parent). Can you do it in O(n2)? In  ? In
? In  ? (I'm pretty certain my approach should work, but I would be glad if anyone could check me on this one. That being said, I'm eagerly waiting for your comments.) Not likely, but maybe you could do even better?
? (I'm pretty certain my approach should work, but I would be glad if anyone could check me on this one. That being said, I'm eagerly waiting for your comments.) Not likely, but maybe you could do even better?
First of all, we'll simplify the problem a bit. Note that after every command the values of x + y and x - y are altered by ± 1 independently. Suppose we have a one-dimensional problem: given a sequence of x's and t's, provide a looped program of length l with commands ± 1 which agrees with the data. If we are able to solve this problem for numbers xi + yi and xi - yi separately, we can combine the answers to obtain a correct program for the original problem; if one of the subproblems fails, no answer exists. (Most — if not all — participants who solved this problem during the contest did not use this trick and went straight ahead to the two-dimensional problem. While the idea is basically the same, I'm not going into details for their approach, but you can view the submitted codes of contestants for more info on this one.)
Ok, now to solve the one-dimensional problem. Let us change the command set from ± 1 to + 0 / + 1: set 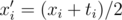 . If the division fails to produce an integer for some entry, we must conclude that the data is inconsistent (because xi and ti should have the same parity). Now it is clear to see that the operation - 1 becomes operation 0, and the operation + 1 stays as it is.
. If the division fails to produce an integer for some entry, we must conclude that the data is inconsistent (because xi and ti should have the same parity). Now it is clear to see that the operation - 1 becomes operation 0, and the operation + 1 stays as it is.
A program now is a string of length l that consists of 0's and 1's. Denote si the number of 1's among the first i commands, and s = sl for simplicity. Evidently, an equation 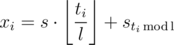 holds, because the full cycle is executed ⌊ ti / l⌋ times, and after that
holds, because the full cycle is executed ⌊ ti / l⌋ times, and after that 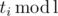 more first commands. From this, we deduce
more first commands. From this, we deduce 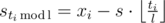 .
.
Suppose that we know what s is equal to. Using this, we can compute all 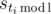 ; they are fixed from now on. One more important fixed value is sl = s. In any correct program si ≤ si + 1 ≤ si + 1, but not all values of si are known to us. When is it possible to fill out the rest of si to match a correct program? If sa and sb are adjacent entries that are fixed (that is, every sc under a < c < b is not fixed), the inequality 0 ≤ sb - sa ≤ b - a must hold (a and b may coincide if for different i several values of
; they are fixed from now on. One more important fixed value is sl = s. In any correct program si ≤ si + 1 ≤ si + 1, but not all values of si are known to us. When is it possible to fill out the rest of si to match a correct program? If sa and sb are adjacent entries that are fixed (that is, every sc under a < c < b is not fixed), the inequality 0 ≤ sb - sa ≤ b - a must hold (a and b may coincide if for different i several values of 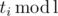 coincide). Furthermore, if the inequality holds for every pair of adjacent fixed entries, a correct program can be restored easily: move over the fixed values, and place sb - sa 1's between positions a and b in any possible way, fill with 0's all the other positions in between.
coincide). Furthermore, if the inequality holds for every pair of adjacent fixed entries, a correct program can be restored easily: move over the fixed values, and place sb - sa 1's between positions a and b in any possible way, fill with 0's all the other positions in between.
The trouble is that we don't know s in advance. However, we know the positions and the order in which fixed values of sa come! Sort them by non-decreasing of a. All fixed sa can be expressed as linear functions of s; if we substitute these expressions in the 0 ≤ sb - sa ≤ b - a, from each pair of adjacent fixed values we obtain an inequality of general form 0 ≤ p·s + q ≤ d, where p, q, d are known values. If the obtained system of inequalities has a solution, we can get ourselves a valid s and restore the program as discussed above.
It suffices to notice that every inequality of the system has a set of solutions of general form l ≤ s ≤ r (if the set is not empty), where l and r should be calculated carefully depending on the sign of p. All the intervals should be intersected, and the resulting interval provides a range of valid values of s.
Overall, the solution works in 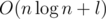 , or even in O(n + l) if we use bucketing instead of sorting. Note that the l summand in the complexity is only there for the actual program reconstruction; if we were only to check the existence of a program, an O(n) solution would be possible.
, or even in O(n + l) if we use bucketing instead of sorting. Note that the l summand in the complexity is only there for the actual program reconstruction; if we were only to check the existence of a program, an O(n) solution would be possible.
Sample solution: 10973870
Challenge (kinda hard). Under the same statement, how many (modulo a prime number) different programs agree with the given data? Assume that all elementary modulo operations (including division) take O(1) time. Can you solve this problem in O(nl)? In O(n + l)? Maybe even better (in 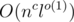 , for example?)
, for example?)
The problem has several possible approaches.
The first approach. More popular one. Forget about t and T for a moment; we have to separate teachers into two groups so that no conflicting teachers are in the same group, and the number of students in each group can be chosen to satisfy all the teachers.
Consider a connected component via the edges which correspong to conflicting pairs. If the component is not bipartite, there is clearly no valid distribution. Else, the teachers in the component can be separated into two sets such that each set should be in the same group, and the groups for the sets should be different. The teachers in the same set will always go together in the same group, so we may as well make them into a single teacher whose interval is the intersection of all the intervals for the teachers we just compressed. Now, the graph is the set of disjoint edges (for simplicity, if a teacher does not conflict with anyone, connect him with a 'fake' teacher whose interval is [0;∞]).
Consider all possible distributions of students; they are given by a pair (n1, n2). Provided this distribution, in what cases a pair of conflicting teachers can be arranged correctly? If the teachers' segments are [l1, r1] and [l2, r2], either l1 ≤ n1 ≤ r1 and l2 ≤ n2 ≤ r2, or l2 ≤ n1 ≤ r2 and l1 ≤ n2 ≤ r1 must hold. Consider a coordinate plane, where a point (x, y) corresponds to a possible distribution of students. For a pair of conflicting teachers the valid configurations lie in the union of two rectangles which are given by the inequalities above. Valid configurations that satisfy all pairs of teachers lie exactly in the intersection of all these figures. Thus, the problem transformed to a (kinda) geometrical one.
A classical approach to this kind of problems is to perform line-sweeping. Note that any 'union of two rectangles' figure (we'll shorten it to UOTR) is symmetrical with respect to the diagonal line x = y. It follows that for any x the intersection of the vertical line given by x with any UOTR is a subsegment of y's. When x sweeps from left to right, for any UOTR there are O(1) events when a subsegment changes. Sort the events altogether and perform the sweeping while updating the sets of subsegments' left and right ends and the subsegments intersection (which is easy to find, given the sets). Once the intersection becomes non-empty, we obtain a pair (x, y) that satisfies all the pairs of teachers; to restore the distribution is now fairly easy (don't forget that every teacher may actually be a compressed set of teachers!).
Didn't we forget something? Right, there are bounds t and T to consider! Consider an adjacent set of events which occurs when x = x1 and x = x2 respectively. The intersection of subsegments for UOTRs obtained after the first event will stay the same while x1 ≤ x < x2. Suppose the y's subsegmen intersection is equal to [l;r]. If we stay within x1 ≤ x < x2, for a satisfying pair of (x, y) the minimal value of x + y is equal to x1 + l, and the maximal value is x2 + r - 1. If this range does not intersect with [t;T], no answer is produced this turn. In the other case, choose x and y while satisfying all boundaries upon x, y and x + y (consider all cases the rectangle can intersect with a 45-angle diagonal strip). Thus, the requirement of t and T does not make our life much harder.
This solution can be implemented in 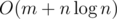 using an efficient data structure like
using an efficient data structure like std::set or any self-balancing BST for sets of subsegments' ends. The very same solution can be implemented in the flavour of rectangles union problem canonical solution: represent a query 'add 1 to all the points inside UORT' with queries 'add x to all the points inside a rectangle', and find a point with the value m.
Sample solution (first approach): 10973887
The second approach. Less popular, and probably much more surprising.
Imagine that the values of t and T are small. Introduce the set of boolean variables zi, j which correspond to the event 'ni does not exceed j' (i is either 1 or 2, j ranges from 0 to T). There are fairly obvious implication relations between them: 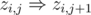 . As t ≤ n1 + n2 ≤ T, we must also introduce implications
. As t ≤ n1 + n2 ≤ T, we must also introduce implications 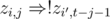 (here i' is 1 or 2 not equal to i) because if a + b ≥ t and a ≤ j, b must be at least t - j, and
(here i' is 1 or 2 not equal to i) because if a + b ≥ t and a ≤ j, b must be at least t - j, and 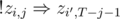 for a similar reason. In this, zi, j for j < 0 clearly must be considered automatically false, and zi, j for j ≥ T must be considered automatically true (to avoid boundary fails).
for a similar reason. In this, zi, j for j < 0 clearly must be considered automatically false, and zi, j for j ≥ T must be considered automatically true (to avoid boundary fails).
The last thing to consider is the teachers. For every teacher introduce a binary variable wj which corresponds to the event 'teacher j tutors the first group'. The implications 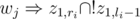 and
and 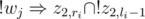 are pretty much self-explanating. A conflicting pair of teachers j and k is resolved in a straightforward way:
are pretty much self-explanating. A conflicting pair of teachers j and k is resolved in a straightforward way: 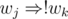 ,
, 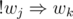 .
.
If a set of values for all the boolean variables described satisfies all the restrictions, a valid distribution can be restored explicitly: n1 and n2 are maximal so that z1, n1 and z2, n2 hold, and the teachers are distributed unequivocally by values of wj. It suffices to notice that the boolean system is a 2-SAT instance, and can be solved in linear time. If we count carefully, we obtain that the whole solution has linear complexity as well: O(n + m + T).
Didn't we forget something? Right! The value of T may be too much to handle Ω(T) variables explicitly. To avoid that, one may notice that the set of possible values of n1 and n2 may be reduced to 0, t, li, t - li, ri, t - ri. We can prove that by starting from any valid values of n1 and n2 and trying to make them as small as possible; the listed values are the ones we may end up with. Thus, we can only use O(n) variables instead of Ω(T). The implications can be built similarily, but using lower/upper bound on the list of possible values instead of exact values (much care is advised!). Finally, this solution can be made to work in 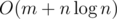 , with the logarithmic factor from all the sorting and lower/upperbounding.
, with the logarithmic factor from all the sorting and lower/upperbounding.
Sample solution (second approach): 10973881
Challenge (easy, for a change) Don't you think it's wrong that a group may be without a teacher altogether? Come up with an algorithm that finds a distribution that places at least one teacher in each group. The complexity should not become worse. How about at least k teachers in each group?
Whew, wasn't it a long run! I tried to be verbose and elaborate where it was possible, hope it was worth the wait. Let me know what you think of this write-up!











In Quasi Binary :
I thinkWow, that sucks hard. Thanks for noticing!
Firstly I apologize for this harsh comment.
Please, in the future, have someone read the English problem statement. It is not the first time a translator screw up singular / plurals. (See 525C - Ilya and Sticks
Ilya decided to make a rectangle from the sticks.but in fact many rectangles can be made)For B, the problem statement still says
Do not have to print the leading zeroshttps://code.google.com/codejam/problem-preparation.html#problem
A programming competition isn't a job interview and it isn't a conversation. If the problem is ambiguous, then a person who interprets it one way is going to get it right and a person who interprets it another way is going to get it wrong (and probably not know why). If the problem is unclear, then the contestant is going to spend valuable time in the contest trying to understand it and asking for clarification. In contests the difference between "b" and "B" is usually "wrong answer" rather than "good enough". This is the wrong context for testing someone's ability to understand and to disambiguate. While unclear and ambiguous puzzles are fun sometimes, it is unfair to reward lucky guesses when it comes to interpreting problem statements.
Even worse, in Codeforces, time and resubmissision penalties are important scoring factors (and there are hacks too!).
Code Jam wrote that?
...
Hahahahahahahahahahaha !! And then they make "Mushroom Monster"... talk about teaching through example.
in problem B quasi binary, instead of checking each number from 1 till 1000000 if its quasi, some guys have used some bitwise tricks to generate all quasi numbers. can someone explain that. thanx.
You can do this using a recursive approach. Suppose you have a function F that takes cnt [counter] and cur [current number].
Base case: If cnt equals 6, this means cur is a 6-digit number (zeros or ones) store it in your array or vector.
Recursive rule: First start with zero. Call F(cnt+1,cur * 10 + 1) and F(cnt+1,cur * 10).
In the end add 10^6, as it's the only 7-digit quasi binary number.
For editorials like this it is worth waiting a day after the contest. Thank you!
I solved problem C in O(n) time... It was not so hard.
Here's a solution in O(n).
10886227
Not in O(n), in O(m) time. It's mush faster than my solution.
What about this? 10891668
your solution will fail on test case
10 2 1 2 10 5
your code is printing 7 but the answer is 8
Indeed! The formula was off, I guess that because of a rounding error in a division by 2. Thanks a lot.
I'm worried at how many more things we believe we got right when in reality there are mistakes not taken into account by the tests.
I've used something like your first approach for H, but both Egor and scott_wu have used a much simpler solution.
In absence of t and T, it's not hard to see that we should set n1=max(li) and n2=min(ri). Now, if n1+n2<t, we should appropriately increase n1, and if n1+n2>T, we should appropriately decrease n2.
I guess that might work, though I don't have an easy explanation why is that always true. Do you have an idea?
I looked at easier versions of the problem in order to develop a proof. Here's my (rough at times) reasoning:
First, let's consider the problem without t, T, or teacher conflicts. Define n1 = max(li) and n2 = min(ri). Note that all ranges with ri ≥ n1 or li ≤ n2 cover n1 and n2 respectively. That means if (n1, n2) doesn't work, then there is some range [li, ri] where ri < n1 and li > n2. The existence of such a range means that n2 < n1. Hence, the range with right endpoint n2, the range with left endpoint n1, and the range described above form three ranges with no intersection, meaning that the set of ranges is impossible. What this essentially means is that (n1, n2) is our "best" solution, since if (n1, n2) fails, the range is impossible.
Now, lets add back in the t and T constraints. We'll look at two cases: what happens when n2 < n1 and when n1 ≤ n2.
When n2 < n1, then any solution (n2', n1') must have n2' ≤ n2 and n1 ≤ n1'. If n1 + n2 < t, then we increase n1, since every time we decrease n2' it can only reduce the number of ranges covered. We can use the same argument for when n1 + n2 > T.
When n1 ≤ n2, all the union of ranges is a single range [n1, n2]. Note one of (n2', n1') must stay within the range if the solution is to be valid. Hence, it makes sense to increase n1, since doing so would make the solution deviate the least from the original (and every deviation is an opportunity for a solution to fail). Again, we can use the same argument for when n1 + n2 > T.
Summarizing, (n1', n2') is our "best" solution. This is because we took the previous best solution (n1, n2) and made the "best" modifications to it. Essentially, if (n1', n2') fails, then any other solution would fail, so the set of ranges is impossible.
Now, we know that it only suffices to check (n1', n2'). Adding teacher conflicts are easy to resolve at this point. We just reduce each connected component into two ranges, and see if we can fit (n2', n1') into them. If we can for all components, then it is possible, else impossible. (Also check for odd cycles.)
P.S. Could someone explain the motivation for the original (n1, n2)?
Thanks for the detailed editorial!
For problem H, I noticed some submissions looked at only one pair of times. It works as follows:
Let x be the maximum start point of all teachers, and let y be the minimum end point of all teachers.
Then, if x+y < t, set x = t-y, and if x+y > T, set y = T-x
Now, if x < 0 or y < 0, there is no solution. Otherwise, we claim that we only need to check that the pair x,y works. To assign teachers, we do the following procedure for each teacher
If we get any conflicts, we return impossible, otherwise for each unassigned teacher, assign them arbitrarily (and set all their neighbors in opposite groups and so on). If we discover a conflict here, return impossible.
Finally, if we have no conflicts, we've discovered a satisfying assignment, so we're done.
Now, my question is, why is it sufficient to only check this single pair? I kind of have a vague idea for why (using some sort of greedy reasoning), but I'm not entirely sure.
EDIT: Never mind, I just saw Petr's comment above :)
There is also one alternative on how to solve inequalities in G. We can find adjacent a and b such that b-a is minimized and then try every value for (s_b-s_a), then we have s and we can check in O(n) if it is good. There is O(b-a) values to try for (s_b-s_a), and b-a is O(l/n), if we do check in O(n) it totals to O(l).
Yeah, nice and easy. Doesn't work if l is large and we want to check the existence of program though. =)
How to solve second problem with dynamic programming?
vector q={ quasi-binary numbers which are < n } dp[1]=1; for(int i=2;i<=n;i++) for(int j=0;q[j]<=i;j++) d[i]=max( d[i] , d[ i-q[j] ]+1 );
At start, you can find all kvazi-binary numbers. We can count ans by using dp: ans[n] = min( at all k:ans[n-k] + 1, where k is kvazi-binary number). You can reestabilish the answer by having an array of parents: for each n we have add[n] and prev[n]: how to get n and from what we can get it. Also you can see my code. Sorry, my English isn't good.
why it is true ans[i] = min(ans[i],ans[n-k]+1)?
Because you can get n by x + k,k is kvazi-binary number. And we have already counted ans[x]. We need to take minimum of all of the able k.
And why +1?
Because you need one adding summand to get n from n-k
This works but could fail on another target string (e.g. CORCES has length 6 but sum of prefixes is 7). For example target string "abababa" could be hacked with "ababa". Of course it's easy to fix this (check len(s) ≥ len(t) or stop when prefix and suffix intersect), but it's sad that CODEFORCES was not vulnerable to this, it could be a nice hack :)
That's right.
Challenge B: I think, the minimum number of summands will be D — V; where, D = number of different digits[except '0'] in 'n' . V = 1 if n's any right part contains only 2 different digits and these 2 digits do not appear in the left part. Else V = 0. Example,
991200787878
here, 787878 part contains only 2 digits and none of these digits appear at left part.
Seems far from the truth. For example 7654321 = 76766 + 7577555, but your answer seems to be at least 6.
For challenge A is there an algorithm faster than O(n — |t|)?
Here is a solution in O(log(n)):
http://codeforces.com/blog/entry/17612#comment-224896
Well, there's still no Tutorial on the contest page Contest materials....
Intresting, i solve D with opposite way. When i found 'x', i calculated corresponding dx dy for all 'o', and tested, can or not piece go in this place. If all pieces hasn't '.' whith this dx dy, it is correct move. When we find correct move, mark all x+dx, y+dy positions, where x, y — position of 'o'. In the end, if we have unmarked 'x' — answer NO
Submission
C for O(m):
Suppose that day #i has number di, day #i+1 has number dj (dj > di), and heights are hi and hr.
So, we can firtsly only go up, then only go down. Suppose we rose to a meters and went down to b meters. Heights are (hi, hi+1, hi+2,..., hj+1, hj). We must maximize a. a+b = j-i by condition. And some days we can not to change height. Hence a-b<=dj-di. So: 1)a+b = j-i; 2) a-b<=dj-di. Hence 2a<=j+dj-(i+di)=>a<=(j+dj-i-di)/2.
Submission: 10897009
I think we've both had the same thought implementing them really differently :) 10891668
Problems have many mistakes in translation :(
Please can someone explain more on how to use BIT on Problem F?
My solution for H was different than either one you said or the one in the comments. Basically, instead of UOTR, which is a 2-dimensional problem, you apply a transformation to create a 1-dimensional problem, then just sort and sweep. No set or segment tree is needed.
Start off like your first solution, but notice that instead of a UOTR, you can use a set of conditions of the form "At least one of n1 and n2 must be in [a,b]" or "Both n1 and n2 must be in [a,b]".
More precisely, if your UOTR is "one of them must be in [a,b] and the other in [x,y]", then the conditions are "at least one of them must be in [a,b]", "at least one of the must be in [x,y]" and "both of them must be in [min(a,x),max(b,y)]". Convince yourself that this is equivalent (the only difficult case is when n1 is both in [a,b] and [x,y] — check that the "both of them" condition guarantees that n2 is in [a,b] or [x,y] in that case).
The "both of them" conditions just give you an upper and lower bound on n1 and n2. The "one of them" conditions can be sorted, and then you sweep through them, having n1 satisfy some lower ones and n2 satisfy the rest. You get some interval for n1 and some interval for n2 and you check that [t,T] can be reached.
I usually post here in Codeforces when I'm angry about a particular contest, like I did with both rounds of Google Code Jam this year.
Well, this time I want to take the chance to congratulate Endagorion for making this round. All problems were beautiful and enjoyable. This is not a coincidence. I was expecting great things from him, since his last contest was also excellent. I hope we will have more contests like this one in the near future.
It's such a pity that it was held on a Sunday afternoon (noon in my country actually). It's probably the only part of the week when I always sleep, so I couldn't take part. I took part virtually a few hours ago and ranked in the top 100.
Let's hope he brings us another awesome round soon!
Really, really good editorial! Setting a new standard hopefully :)
I guess that D challenge can be done by some 2D FFT (I think I've heard about existence of such, but didn't give it a thought)
1D FFT is enough, just pad the board with zeroes at the right and concatenate all rows.
Haha, you're absolutely right :). That is a perfect confirmation of what I was talking about in a comment below this one :D. The moment when someone comes up with any possible solution, probably completely tedious one, is not a moment when he should stop thinking about better approach :D (which is, as can be seen, often situation in my case :P)
Wow, when I got E accepted it was ~0,5h left and I read H, came up with solution with UOTR's almost immediately but felt helpless given that I have ~25 mins to code it, so I didn't do anything of any use during the rest of the contest, but seeing Petr's and W4yneb0t's comments ( http://codeforces.com/blog/entry/17612#comment-224607 and http://codeforces.com/blog/entry/17612#comment-224693 ) I think that I should never give up :)!
What I want to add is that H was pretty hard problem in itself and out lifes were made even more difficult because of many technical unnecessary issues. First thing is to restore the result and second thing were big coordinates. I understand that restoring result is a typical demand, especially when it comes to problems with binary answer (like POSSIBLE/IMPOSSIBLE), because that makes tests much more reliable, but I see no reason in making coordinates so big. It is obvious that we should scale them and that provides many not-nice-to-code-things, moreover t and T can't be scaled in that same manner, so blaaaahh... Completely unnecessary difficulty, making codes much more uglier and not making problem more interesting at any angle.
Btw it is my third post in a row, but since they regard to different matters I think it's not a bad thing to keep them separate :P.
In problem H, restoring the teachers after you have n1 and n2 is trivial but tedious. It's completely unnecessary to demand anything except n1 and n2, demanding the restoration doesn't help you distinguish wrong solutions. Coordinate compression doesn't work like you'd want it to because of the t and T, but I'm not sure if small coordinates would make it conceptually easier — any ideas?
On the other hand, this is not a math contest, it's a programming contest, and programming tedious boring things is still programming. That sounds terrible now that I say it, but if I don't, someone else will.
i think an editorial is good when it only give several words but give people inspiration , but through your editorial i have an illusion of reading a documentary film! however problem is very interesting , i only think that codeforces do not need imitate topcoder to make a longgggg editorial!
So what do you want? Sereja tutorial?
Or maybe you wanted this tutorial.
I think long tutorial is good because it explains all necessary concepts, so it's easy to understand it. Besides, the point of editorial is to let people who didn't get problem understand the solution. So, it should be clear and easy to understand.
Could somebody explain, please, how to solve Challenge B?
my O(n*log^3(n)) solution for F gave TLE during the contest :(
O(n * log3(n)) ???
That complexity surely gives TLE for values of N up to 2 * 105, but why the extra logarithmic factor? I did it with O(n * log2(n)).
I wouldn't say "surely", but one should definitely consider such possibility. It could depend on constant factor.
log(2 * 105) = 18, so O(n * log3(n)) would mean around 2 * 105 * 183 = 1166M. I can't imagine 1166 M operations, even with the lowest constant factor, running in under 3 seconds, unless it is ran on an ultra fast server.
I once tried to hack one guy in TC doing explicitly 10^9 operations where TL was 1 or 2s and my hack attempt was unsuccessful, because "these were light arithmetic operations". log3 sounds like something where many operations can be not done in each attempt, probably instead of doing ~8000 ops as it should have it often makes sth like 1000 operations — I didn't look at the code, but it could be the case.
Do not forget that there ln(n), not log(n), so it could pass:10910881
Can anyone tell me more about pro E? I don't understand what tutorial says. Thanks in advance
make two array dp_max[u],dp_min[u].
1. dp_max[u]=x means if current player is in node u and he can take the xth largest number in the subtree of u.(the current player always want the 1th largest number)
2. dp_min[u]=x means if current player is in node u and he can take the xth largest number in the subtree of u.(the current player always want the (siz)th largest number)(siz means the size of subtree of u)
3. dp_max[u]=min(dp_min(v)) (v is child of u)
4. dp_min[u]=sigma(dp_max(v)-1)+1
it seems "4" is not easy to get .
just think this way, suppose the current player is in node u, and for all its child v ,dp_max[v] has been got,just regard it as a constant ,because we are going to use tree dp, so its child can get through recursive. The player wants to make dp_min[u] as large as possible, so for every child he can fill the top largest number(1,2,3...) in the space to make the Opponent can never get it , so that the number he put into the "unsafe" space is as large as possible! we call the space is "safe" when the player can never get it. for every child v , its safe place is dp_max[v]-1 !
I learn this problem from dreamoon_love_AA , if you can read chinese you can check this Your text to link here...
Here is some explain for maximizing the answer (minimizing is about same concept)
First for a node v, it has k children, namely u_1, u_2, ... u_k
node v's leaf number w(v) is summation each children's leaf numbers
so w(v) = sum(w(u_i)), 1<=i<=k
Define dp_max(v) and dp_min(v) be the index of the maximum/minimum number out of sorted w(v) numbers, remember it is index, so it is always in [1, w(v)]
For dp_max(v):
you got dp_min(u_1), dp_min(u_2) ... dp_min(u_k) in your hand
all dp_min(u_i) is in range of [1, w(u_i)]
To set up an arrangement to maximize dp_max(v), you can try to put the largest w(u_i) number in u_i's leaf, out of w(v) numbers.
For example, let w(v) = 10, w(u_1) = 3, w(u_2) = 7
dp_min(u_1) will give you an answer in [1,3], dp_min(u_2) will give an answer in [1,7]
but they are mapping to [8,10] and [4,10] respectively.
So you have to do a mapping...which is w(v) — w(u_i) + dp_min(u_i), and you take the maximum of all u_i
For dp_min(v)
See the image below
Say v has these 3 children, total has 7+4+10 = 21 leafs, and by dp_max(u_i), 1<=i<=3, the children gives 5, 2, 10 as answer
What does that means? it's the INDEX of the sorted list of numbers...
For example, the 5 from the first subtree (dp_max(u_1)) means the fifth largest number out of 7 numbers
it can be 9 in [1,3,4,7,9,11,12], or 5 in [1,2,3,4,5,6,7]... it's the index
Now how can we arrange the number to maximize the result? Here the player will take minimum of all dp_max(u_i)
First, that means you are picking one of the red circles,
so 1. the number on the right of any red circles and 2. the other red circles' number
have to be larger than the one you pick.
This is the only constrain, you cannot do better than that, which means ALL numbers on the left of ALL red circles can be smaller than your number
So out of [1, w(v)] numbers, actually the largest you can get for dp_min(v) is sum (dp_max(u_i) — 1) + 1
dp_max(u_i) — 1 is the numbers on the left of any red circles, the last + 1 is the red circle you pick exactly
Using the image as example, the best you can choose is (4 + 1 + 9) + 1 = 15, out of 21 leafs
Can someone better explain the proof of the upper bound of O(N * sqrt(N)) of the second approach to problem F? I came up with the same solution but at the beginning I thought it was tle...
For this part I think the tutorial is quite clear, I try to explain in my own words:
For each v, for some k, its parent p = floor( v-1 /k ), and by the inequality property of floor function, you can deduce that floor(v-1 / p+1) < k <= floor( v-1 / p), given that p is a parent for (v, k) pair.
Now the total number of different p of v, for ALL k, is O(sqrt(v)), because:
Case 1: for k >= sqrt(v-1), floor(v-1/k) will fall into range [0,sqrt(v-1)]
Case 2: for k < sqrt(v-1), floor(v-1/k) will AT MOST has sqrt(v-1) different values
Combine Case 1&2, total # of parent for a v, for ALL k, is O(sqrt(v))
For each node v > 0 (0-based), we find all parents of v (O(sqrt(v)) of them), and update the range for k of each parent (O(1) using delta encoding), there are n different v, so total complexity is O(n * sqrt(n))
Here is my code with some comments, hope it helps 10935054
PS1: Can someone explain more on approach 1 though, my original thought is approach 1 but cannot figure how to apply BIT / segment tree...
Can anyone please try to explain me the solution for E ? I've codding seems pretty easy but I just can't figure out what dp[node][player] exactly stands for and how it works.
Here's the solution "I implemented" 10933756
Something I don't get in problem E editorial:
1) What does n(i, j) mean?
2) Does dpmax, dpmin equal to dmax, dmin?
make two array dp_max[u],dp_min[u].
1. dp_max[u]=x means if current player is in node u and he can take the xth largest number in the subtree of u.(the current player always want the 1th largest number)
2. dp_min[u]=x means if current player is in node u and he can take the xth largest number in the subtree of u.(the current player always want the (siz)th largest number)(siz means the size of subtree of u)
3. dp_max[u]=min(dp_min(v)) (v is child of u)
4. dp_min[u]=sigma(dp_max(v)-1)+1
it seems "4" is not easy to get .
just think this way, suppose the current player is in node u, and for all its child v ,dp_max[v] has been got,just regard it as a constant ,because we are going to use tree dp, so its child can get through recursive. The player wants to make dp_min[u] as large as possible, so for every child he can fill the top largest number(1,2,3...) in the space to make the Opponent can never get it , so that the number he put into the "unsafe" space is as large as possible! we call the space is "safe" when the player can never get it. for every child v , its safe place is dp_max[v]-1 !
I learn this problem from dreamoon_love_AA , if you can read chinese you can check this Your text to link here...
Can you say more about why dp_min[u]=sigma(dp_max[v]-1)+1 . In my oppinion , i think dp_min[u]=max(dp_max[v]-1) . Can you explain for me pls
I have a solution for Challenge in problem A in O(log(n-t)) but i have no way to test it
Could u provide any test cases or anything to be able to test my solution :D
Thank you :)
My solution:
int ans,left=n-t.size(); if(n<=t.size()) ans=0; else ans=power(26,left)+25*power(26,left-1)*t;
It can be easily modified this solution to handle modulo
Thanks :)
Your formula seems correct to me. Good job!
Care to share your reasoning?
It is obvious that if n<t.size() the ans wiil be 0
but if n>t.size()
we will show it by example (without losing generality)
assuming that t="abc" and n=5 (a is the first character of t , b is the second character of t, ... )
if we put the whole string t at beginning we can put power(26,n-t.size()) = power(26,2) characters
but we need also to try to put t.size()-i characters at the beginning and i characters at the end for (all 1 <= i <= t.size())
at i=1 put 2 characters of string t at beginning and 1 character of string t at end it will be "ab c" , we previously calculated this case "abc " , now we need to calculate this "ab c" . If we put 'c' in the first space (third letter) we will have duplicates because we already calculated all strings that starts by "abc" so in order to ensure we calculate every string once we will need to let first space any character other than 'c' and for the rest of characters will be any possible character so it will be 25 for first space multiplied by power(26,n-t.size()-1) for the rest of spaces (because changing first space (third letter) into any character other than 'c' it will be different than all strings we calculated before and we have already calculated all strings that have 'c' in the third character and "ab" are common in the last cases).
the same can be proved for each i and range of i is 1<=i<=t.size()
so the answer of all i will be t*answer of one i = t*(25*power(26,n-t.size()-1)
the final answer will be power(26,n-t.size()+t*(25*power(26,n-t.size()-1)
i hope i explain it well enough :D
Thanks :)
could anyone please explain why my code 11342547 and 11342593 keep doing things wrong at case 24?
we can solve Quasi Binary in O(L)
where L is number of digits n
code
in the problem: Quasi Binary I'm sending a right solution but i got WA, on my computer the code gets the correct results for the cases, but when i send it i got WA on case 4.
http://codeforces.com/contest/538/submission/15132451
How do I solve Quasi binary using dp ? I solved it in O(n), but i want to learn dp.
Bump, I would like to know how to implement dp for this question too for practice.
I wrote a reference solution with some comments: 22011133, hope it's helpful.
can someone help with the Problem B CHALLENGE part?Thanx!