mariabauza and I are trying to do the Travelling Salesman Problem in a segment graph (for a real life application, it's not a CP problem): you are given 10-100 segments in the plane you have to color (go through), give the shortest path to color them all.
For example, here are 2 possible paths (in red) for the same segments, one shorter than the other.
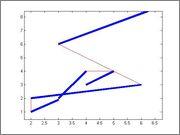
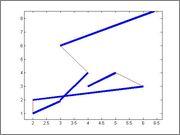
To do it we use the 2-opt algorithm we learned in Petr's blog. There he explains that the 2-opt algorithm works very well, finding the best solution in very few tries. However, with only those 5 (random) segments it only finds the optimal solution 26% of the time after 400 restarts (finding only local minimums during 400 tries, 74% of the time).
Do you think the algorithm may not be as effective for the fact we are now dealing with segments and not points? Or are you sure the algorithm should work almost perfectly and we must have some bug? (We have looked our code thoroughly before posting here, but you never know) Can it be slightly modified to work better in this kind of graph?
Finally, we know that we can develop TSP algorithms for Euclidean graphs, but the only one we know (using the MST) doesn't quite apply when dealing with segments. Do you know/can you come up with any other algorithm that could help?
Thanks!











In the cases it didn't found the optimal solution, how close was it (that is, how worst was the solution found)? I think that 26% it's normal since some optimal solutions can be more "tricky".
Are you only interested in find the optimal solution, or in finding the best approximation possible? If you just want the best approximation try to use simulated annealing (and maybe using not only 2-opt but also k-opt), it works greatly on a general Euclidean TSP and should work in your version too since your version is an euclidean TSP with some fixed edges.
About the initial solution generator, have you tried to connect the segments in a greedy way like adding an edge between the closest segments first?
Hope my answer helps :)
Yes; we are starting from a greedy solution (when we started from a random one in a big testcase the results were poor) and indeed most (though not all) the solutions given are reasonably good. We'll probably try simulated annealing, thank you!
there is a 1.5 opt algorithm for TSP metric too.
it solved by using MST and minimum weighted matching.
At first I thought something similar but then I thought the following: suppose we had A = (0,0)-(0,1), B = (0,1)-(0,2), C = (0,2)-(0,3) then |AB|+|BC| (as segments ) = 0, but |AC| = 1; thus it doesn't satisfy the metric inequality.
On the other hand we are working on Euclidean space and, as you suggest, it seems things should be metric, what is wrong then with my example?
Maybe you want to check out Christofides algorithm.
It really depends on your constraints. Can you use existing tools? How much processing power do you have per problem? Do you want optimal answers?
If you can use existing tools then you could use LP solvers. There are also several existing libraries for TSP, maybe you could try to modify one of them.
If you want to write something simple from scratch, then use SA with 2-opt or use HC with v-opt/k-opt/Lin-Kerninghan. 2-opt is very weak (even with restarts) and is never used in practice. Your initial solution doesn't matter at all. I'm guessing that SA with a correct temperature schedule should give you optimal solutions within less than a second for cases with ~100 segments.
First of all, thanks for your answer! I didn't understand 2 things:
what does HC stand for? The only related thing I could find is 'Hamiltonian Cycle' which for me is a problem, but not an algorithm.
With 'Your initial solution doesn't matter at all.' are you refering to 2-opt or SA? Gramatically it seems that 2-opt, but I thought that in 2-opt if you start very near to a local minimum you'll probably end up there.
To the questions about your constraints: we would prefer not using existing tools, processing power is quite limited (matlab on a PC, expecting an answer in at most 5s), but we don't need optimal answers. In this case, would you go with SA with 2-opt? :)
HC = Hill Climbing.
I was just spewing sentences in a random order :) Initial solution doesn't matter if you have a decent algorithm. Random is absolutely fine.
Why matlab? Isn't it ~100x slower than any compiled language (which actually could be an issue here). Anyway, I would definitely go with SA with 2-opt considering, since implementing it takes 5-15 minutes. If it doesn't suffice you (which I highly doubt), then I would probably made sure that my SA really works correctly and optimize it first (O(1) evaluation, neighbors list for state transition, etc).
Edit: Also, since you're using matlab, you can actually use LP (ILP/MIP) solver since I'm guessing that matlab already has one.
We use Matlab because we have to send instructions to process images and send instructions to arduino; it's very easy to do both things with Matlab.
We'll do SA with 2-opt then, thank you for your advice!