Предсказание Панорамикса (задача A, 2-ой дивизион). Автор задачи - Alex_KPR | ||
| В начале условия задачи подробно описано, что называется простым числом, и что называется следующим после x простым числом. Суть задачи сводилась к тому, чтобы проверить, является ли m следующим после n простым числом. Поскольку n гарантированно простое, нужно проверить два случая: 1. Число m является простым, и 2. Между n и m нет других простых чисел Действительно, если между n и m есть некоторое простое число k, то m уже никак не может быть следующим после n простым. Ограничения в этой задаче небольшие, поэтому решать её можно следующим способом: for(int i=n+1;i<=m;i++) где prime(i) - любая возможная проверка числа на простоту. Другое простое решение этой задачи - учесть тот факт, что ограничения не превышают 50. Можно найти все пары чисел n и m вручную и написать решение в виде серии условий, примерно так: if (n==2 && m==3) return "YES"; Такое решение тоже проходило все тесты. | |
| Асимптотика зависит от конкретной реализации и варьируется от O(1) до O(n + m). Если вы не знаете, почему ваше решение получает вердикт "wrong answer", то возможно, вам стоит проверить своё решение на тесте "2 5". |
| Депрессия (задача B, 2-ой дивизион). Автор задачи - Marishka | |
| Первое, на что нужно обратить внимание - при движении одной стрелки другая остаётся неподвижной. Фактически, это означает, что теперь нам нужно решить две подзадачи: 1. Определить, на какой угол повернуть минутную стрелку, и 2. Определить, на какой угол повернуть часовую стрелку В условии сказано, что стрелки-усы Когсворта двигаются равномерно и непрерывно. Это значит, что при любом, даже очень малом увеличении времени Δt и часовая, и минутная стрелка сдвинутся на некоторые углы. Поскольку число минут всегда целое благодаря формату HH:MM, то каждая минута будет добавлять ровно 360 / 60 = 6 градусов. В свою очередь, на угол поворота часовой стрелки влияет и количество часов, и количество минут. Каждый полный час будет добавлять 360 / 12 = 30 градусов, а каждая минута - (360 / 12) / 60 = 0.5 градусов. Таким образом, нужно суметь вырезать из первоначальной записи HH:MM количество часов и количество минут, после чего применить описанные выше формулы для нахождения ответа. Также нужно обратить внимание, что аналоговые часы не различают время до полудня и после полудня, поэтому ответы для 08:15 и 20:15 будут совпадать. | |
| Асимптотическая сложность решения - O(1). Если вы не знаете, почему ваше решение получает вердикт "wrong answer", то возможно, вам стоит проверить своё решение на тестах "20:15" и "00:00". |
| Герои (задача C, 2-ой дивизион; задача A, 1-ый дивизион). Автор задачи - Alex_KPR | |
| Поскольку героев всего k = 7, а групп три, то задачу можно решать полным перебором. Для этого рассмотрим все случаи размещения героев в каждой из трёх групп и выкинем из рассмотрения некорректные разбиения - такие, при которых хотя бы одна группа оказывается пустой. В каждом из корректных разбиений найдём значения обоих критериев разделения на группы - разницу в опыте между персонажами, которые получат максимальное и минимальное количество опыта, и суммарное количество симпатий во всех группах. Из всех этих способов осталось выбрать наилучший и выдать в качестве ответа. | |
Сложность алгоритма - O(3k· k2). |
| Сброс наковальни (задача D, 2-ой дивизион; задача B, 1-ый дивизион). Автор задачи - dagon | |
| В этой задаче нужно было определить вероятность того, что уравнение Для этого необходимо и достаточно чтобы дискриминант D = p - 4q был не меньше нуля. Для решения этой задачи можно было нарисовать на плоскости (p, q) прямоугольник с вершинами в точках (0, - b), (a, - b), (a, b) и (0, b) и линию p = 4q. Каждая точка прямоугольника соответствует возможным значениям p и q, а линия делит всю плоскость на две части - где уравнение имеет действительные корни, и где оно их не имеет. Тогда вследствие равновероятности и независимости выбора p и q ответ есть площадь пересечения прямоугольника с областью p ≥ 4q, отнесенная к площади самого прямоугольника, в случае его невырожденности (a, b ≠ 0). Если ровно одно из чисел a или b равно нулю, прямоугольник вырождается в отрезок, и искомая вероятность равна отношению длины пересечения отрезка с областью p ≥ 4q и всего отрезка. В случае a = b = 0 ответ на задачу, очевидно, равен 1. |
|
Асимптотическая сложность решения - O(t). Если вы не знаете, почему ваше решение получает вердикт "wrong answer", то возможно, вам стоит проверить своё решение на мини-тестах "0 1", "1 0" и "0 0". |
| Боброжуй-0xFF (задача E, 2-ой дивизион; задача C, 1-ый дивизион). Автор задачи - Marishka | |
| Допустим, что, находясь в вершине v, можно для каждого её прямого потомка vi найти пару значений < xi, yi > , где xi - максимальное количество бобров, которое может съесть боброжуй, стартуя из вершины vi и возвращаясь в неё же, а yi - количество бобров, которое останется в вершине vi после того, как её посетил боброжуй. Отсортируем всех потомков vi по убыванию значения xi и будем посещать этих потомков vi в отсортированном порядке, пока гарантированно сможем вернуться к корню. Если же после посещения всех поддеревьев в вершине v ещё остались несъеденные бобры, то будем продолжать поедание по следующему принципу: выберем потомка с ненулевым значением yj, сделаем прыжок в эту вершину vj и сразу же вернёмся обратно. Такую операцию нужно повторить максимальное количество раз. Естественно, процесс нужно не эмулировать, а осуществить min(b, yj) раз, где b - оставшееся количество бобров в вершине v. Таким образом сформирована пара < x, y > для вершины v по известным значениям < xi, yi > для её непосредственных потомков, где x - количество бобров, которое удалось съесть, а y - это b, количество оставшихся бобров в вершине v. Ответ - это значение x для стартовой вершины s. |
|
Асимптотическая сложность решения - O(n· logn). Если вы не знаете, почему ваше решение получает вердикт "wrong answer", то возможно, вам стоит проверить своё решение на тесте, в котором дерево состоит всего из одной вершины. |
| Ковёр-из-домино (задача D, 1-ый дивизион). Автор задачи - Alex_KPR | |
| Заметим, что каждая клеточка ковра-из-домино находится в одном из трёх состояний: 1. На неё можно поставить как горизонтальную, так и вертикальную кость домино 2. На неё можно поставить только горизонтальную кость домино 3. На неё можно поставить только вертикальную кость домино Неважно, какие значения записаны в каждой клеточке, важны только их состояния. Теперь заметим, что если в какой-то паре соседних столбцов j и j + 1 горизонтально расположена кость домино, то эту пару столбцов размера n × 2 можно вырезать из общего ковра, не побоясь разрезать какие-либо другие кости домино. То есть, эта пара столбцов может заполняться фишками домино независимо от других столбцов. Если n чётно, то могут заполняться независимо не только пары соседних столбцов, но и столбцы единичной ширины, причём единственным способом - размещением всех костей домино в них вертикально. Получаем следующую формулу: dj = (dj - 2· qj - 2) + (dj - 1· pj - 1), где j - количество обработанных столбцов, pj - количество всех возможных способов заполнить костями домино только j-ый столбец (это значение будет равно нулю или единице), а qj - количество всех возможных способов заполнить только j-ый и j + 1-ый столбцы. Очевидно, что эта формула неверна: если некоторую соседнюю пару столбцов можно замостить только вертикальными костями домино, то этот способ посчитается дважды. Воспользуемся тем фактом, что это - единственный случай, когда первоначальная формула не работает, и улучшим её, учитывая этот случай. Получаем: dj = (dj - 2· qj - 2) + (dj - 1· pj - 1) - (dj - 2· pj - 2· pj - 1). В dm будет находиться искомый ответ. Осталось посчтитать значения pj и qj. pj находится достаточно просто: если n чётно и в столбце j нет клеточек, находящихся в состоянии "сюда можно ставить только горизонтальную кость домино", то ответ 1, иначе 0. qj считается классической динамикой: будем на каждом шаге пытаться ставить либо одну горизонтально расположенную кость домино, либо две вертикально расположенных, пользуясь информацией о том, в каких состояниях находятся исследуемые клеточки ковра. Также, нужно все вычисления аккуратно производить по требуемому модулю. | |
Асимптотическая сложность решения - O(n· m). |
| Марсианская кухня (задача E, 1-ый дивизион). Автор задачи - dagon | |||||
| Задача решалась с помощью преобразования инверсии. Инверсия - это преобразование, переводящее точку с полярными координатами (r, φ) в точку Пусть тарелка является кругом с координатами центра (R, 0) и радиусом R, а Гондурас - кругом с центром в (r, 0) и радиусом r. Тогда Гваделупа и Бультерьеры будут расположены так, как показано рисунке слева:
Применим преобразование инверсии. Тогда край тарелки перейдет в прямую |
| ||||
Асимптотическая сложность решения - O(t). |



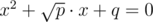 имеет хотя бы один действительный корень, при условии что величины
имеет хотя бы один действительный корень, при условии что величины 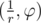 . Утверждается, что инверсия переводит прямые или окружности в прямые либо окружности. Причем образом может быть прямая тогда и только тогда, когда исходная прямая или окружность проходила через начало координат (центр инверсии).
. Утверждается, что инверсия переводит прямые или окружности в прямые либо окружности. Причем образом может быть прямая тогда и только тогда, когда исходная прямая или окружность проходила через начало координат (центр инверсии).

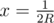 , а край Гондураса
, а край Гондураса 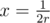 , Гваделупа и Бультерьеры станут окружностями, как показано на другом рисунке. На картинке, получающейся после инверсии, найти образ
, Гваделупа и Бультерьеры станут окружностями, как показано на другом рисунке. На картинке, получающейся после инверсии, найти образ 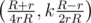 . Чтобы найти радиус Бультерьера, проведем прямую, проходящую через начало координат и центр его образа, найдем две точки пересечения. Можно показать, что прообразы этих точек есть диаметрально противоположные точки на бультерьере. Соответственно, ответ есть половина расстояния между прообразами найденных точек.
. Чтобы найти радиус Бультерьера, проведем прямую, проходящую через начало координат и центр его образа, найдем две точки пересечения. Можно показать, что прообразы этих точек есть диаметрально противоположные точки на бультерьере. Соответственно, ответ есть половина расстояния между прообразами найденных точек.







Автору спасибо за задачи и разбор!
> Отсортируем всех потомков vi по убыванию значения xi
> Асимптотическая сложность решения - O(n).
Вы умеете сортировать за O(n)?
Разбор задачи B 360/60 = 5 :D
Дальше читать разбор задачи B не стал)
А если серьезно, то ни на одном серьезном соревновании такие задачи давать нельзя.
Например, варианты:
1. Х знает эту задачу. Время ее решения будет практически 0.
2. Х пришел первый раз на соревнования по программированию с межнара по математике и читает эту задачу первой. Он набирает баллов примерно как решивший А+В+С (потому что А+В+С надо еще написать же, не забыв аккуратно посмотреть ограничения в В). Смешно, не так ли? За одну строку кода.
и т. д.
Я бы ни слова не возразил против этой задачи, не будь в ней количества тестов - если бы в ней можно было бы просто применять численные методы для построения цепочки окружностей.
Я против того, чтобы задача на математику в одну формулу стоила 1/3 соревнования.
Поэтому, ИМХО, такие задачи лучше всего давать на ACM.
А хотя кто знает, может это на старших курсах будет. Но я сомневаюсь
Upd. Нет, пожалуй, я уверен, что не пройдёт. Возможно, даже если свернуть мозг и вывести аналитическую формулу, то всё равно не пройдёт.
А про подбор закономерности - вообще сомнительно, что такие задачи допустимы. Я, возможно, неправ, но я придерживаюсь мнения, что любая задача на контесте по правилам ACM или вроде того должна быть такой, что человек с мозгом, калькулятором и набором шпаргалок может полностью придумать и доказать её решение столь же быстро, сколь и тот же человек с мозгом, компьютером и Интернетом. Конкретно - я изменю своё мнение (и буду благодарен за информацию), если мне кто-нибудь покажет задачу на подбор закономерности с финала ACM. То, что на последних четырёх полуфиналах NEERC таких задач не было, - это я знаю точно.
По-поводу подбора закономерности.
Во-первых, я не писал о соревнованиях высокого уровня. Естественно, что там особые требования к задачам.
Во-вторых, если Вы считаете, что такие задачи не допустимы, то я готов охотно с Вами согласиться. Это просто был пример, когда основное решение за О(1), но в процессе решения задачи программировать все-таки надо.
Я не знаю, что такое идеальная задача в спортивном программировании, тем более не знаю из чего они возникают, но точно никогда не ассоциировал задачи с контестов с какими-то производственными или другими реальными процессами.
Конечно, задача может быть из реальной жизни, но на её качество, по-моему, это никак не влияет.
Ну, я рассуждал по аналогии. Просто помню, что в знаменитой в некоторых кругах книжечке Козела, где рассказаны все гласные и негласные правила проведения всероссийских олимпиад по физике, было написано, что задачи берутся изначально реальные, а не просто головоломки. Типа так олимпиада куда больше соответствует своей миссии. Было бы логично предположить, что у ACM (у IBM) такие же идеи.
Математика, конечно, должна быть на контестах, но она должна быть именно такой. чтобы надо было посидеть и подумать. А здесь же, если ты знаешь метод, то дальше все элементарно, не знаешь - извини, иди учись.
Хотя да, образовательную ценность у этой задачи отрицать нельзя =)
Но мораль-то понятна: учиться, учиться и учиться...
Тарас, ну вот что ты заладил =)
Ты ещё скажи, что можно рассказать человеку понятие графа (вершины, рёбра, веса рёбер), а потом дать задачу на алгоритм Дейкстры =) Ну а чего, пусть "попробует посидеть и повыводить" -- он же знаком с понятиями =)
В том-то как раз и соль, что преобразование инверсии -- это тоже в некоторой степени метод. Идея метода Дейкстры -- брать вершины в определённом порядке и релаксировать дуги, выходящие из них; идея инверсии -- преобразовать комплексную плоскость. А придумывание таких методов дорогого стоит =)
А задачи в стиле "если ты знаешь метод, то дальше все элементарно, не знаешь - извини, иди учись (с)" очень огорчают. Креативность же должна быть: у авторов при составлении, у участников при решении.
To problem E — Martian Food, I suggest to watch the video "Epic Circles" of Numberphile in youtube in order to get a better explanation and concepts about inverse circles
242986607 I solved the A problem like that. I hope it might help someone one day.