We can find all information about i-th car collisions in the i-th row of the matrix A. More specific, if there is at least one 1 or 3 at i-th row, then i-th car isn't good (it was turned over in at least one collision). Otherwise, i-th car is good. We just need to check this condition for each car.
One can see, that if si = ti for some i, then the value of pi isn't important for us. Really, if we make pi equal to si then it also be equal to ti. And if we make pi not equal to si then it also be not equal to ti. So, we have an answer that is closer or further to both of s and t.
So we interested about such position i that si ≠ ti. If we make pi equal to si we make p further from t. If we make pi equal to ti we make p further from s. It means that we need to divide these positions into two equal parts to have equidistant string. For example, we can make first of these positions closer to s, second closer to t and so on. If the number of these positions is even, we find an answer, if it is odd, answer doesn't exist.
Time complexity — O(n).
One can solve this problem using dynamic programming or greedy algorithm. Start with DP solution.
Define stayi, lefti and righti as maximal count of trees that woodcutters can fell, if only trees with number from 1 to i exist, and i-th tree isn't cutted down, i-th tree is cutted down and fallen left, i-th tree is cutted down and fallen right correspondingly. Now we can compute this values for each i from 1 to n by O(n) time because for each next we need only two previous value. Answer is maximum of stayn, leftn, rightn.
Also this problem can be solved by the next greedy algoritm. Let's fell leftmost tree to the left (it always doesn't make an answer worse). After that, try to fell the next tree. If we can fell it to the left, let's do it (because it also always doesn't make an answer worse). If we can't, then try to fell it to the right. If it is possible, let's do it. Last step is correct because felling some tree to the right may only prevent the next tree's fallen. So we may "exchange" one tree to another without worsing an answer.
Time complexity — O(n).
We can solve this problem by greedy algorithm. Let's prove that it is always possible find an answer (queue with the maximal number of not disappointed people), where all not disappointed people are at the begin of queue. Assume the contrary — there are two position i and j such that i < j, persons at position from i to j - 1 are disappointed, but j-th person isn't. Then just swap persons at positions i and j. After that all persons from i to j - 1 will be still disappointed (or become not disappointed) and j-th person will be still not disappointed. So the answer isn't maked worse.
So, we need to find person with minimal ti, that can be served now and will be not disappointed. We can do that by sorting all the people by time ti and try to serve them one by one. If somebody will be disappointed, we may send he to the end of queue, and doesn't add his serve time to the waiting time.
Time complexity — O(n + sort).
It's true, that Dijkstra modification, where in case of equal distances we take one with shorter last edge, find an answer.
For prove that let's do some transformation with graph. At first, find all shortest paths from u to other vertices. Define di as the length of shortest path from u to i. After that, we can delete some edges. Specifically, we can delete an edge with ends in x and y and weight w if |dx - dy| ≠ w, because it isn't contained in any shortest path, so it isn't contained in shortest path tree. After that, we can direct all edges from vertices with less distance to vertices with greater distance (because of all weight are positive). It's easy to prove, that if we take one edge that entering each vertex, we have a shortest path tree. Then we only need to take for each vertex minimal egde, that entering this vertex. Why? Because we have to take at least one edge, that entering each vertex to make a graph connected. We can't take edges with less weights than minimal. And if we take minimal edges, that entering each vertex we will have an shortest path tree. So that is minimal possible total wieght of shortest path tree.
You can see, that Dijkstra with modification do exactly the same things.
Time complexity — 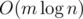











Thank you for the editorial. I ended a 4-hour contest about one and a half hour ago, and I'm not that good at greedy, so I hope I can get a better score next time...
how did u improve in greedy sir , any tips ?
I think time complexity of D is O(n log n) due to sort.
I think we don't count 'sort' in when we calculate time complexity.
on the contrary, we do count 'sort' while calculating time complexity.
thx
Thanks, fixed.
For Problem E, there is a O(m) solution by using SPFA algorithm.
Wow! Could you tell me this method?
You may read about SPFA here.
Actually, SPFA does not run in O(m) time complexity. It's just really fast on random-generated testcases, and in other special cases, it can be O(nm), the same as the original Bellman-Ford.Not a good choice on some platform which allows hacking, isn't it? :P
man, next time no 'greedy'
what is wrong with 'greedy'?
Because too much of everything is bad.. Eg me commenting too much
Can someone explain how to approach problem E ? I didn't quite get it from editorial. i.e What it means by saying where in case of equal distances we take one with shorter last edge . Thanks in advance.
Running the dijkstra's algorithm gives you a tree with minimum distances from source to any other vertex ( tree rooted at source ). Suppose this case :
Now if we have to make a choice between these two in terms of minimum distance, we can see that choosing either is fine. But in case of forming the tree with minimum weight , we need to minimise sum of edge weights. If we choose A->B and A->C , it is a valid dijkstra tree with sum of edges = 3 , whereas choosing A->B and B->C is also a valid tree with sum of edges = 2. So whenever distance is same during relaxation in dijkstra, choose the smaller edge.
Did you mean that we have to find MST here?
sorry , edited. We dont have to find the MST. Rather we have to find a spanning tree which satisfies dijkstra. If multiple trees are possible, then the one with minimum cost should be taken.
Cant you just consider the weights to be the distances between the nodes and run a normal Dijsktras on it.
It would be easier if you read my explanation above once and read up my code : 11189526 .. I have added lots of comments in the code to make it clear for everyone to understand.. Feel free to ask doubts.
A test case where normal dijkstra might fail :
1 2 1
2 3 1
1 3 2
source : 1
Here you can go from 1->3 in cost 2 , but you should select 1->2->3 instead of 1->2 and 1->3 in your tree. You can easily see that both the solutions are valid dijkstra trees.
'maked worse'?
Can anyone tell me why this solution gave WA for test 11 question C? I used DP where prev=0 means previous tree wasn't cut, prev=1 means previous tree was cut to left, prev =2 means previous tree was cut to right Solution Also I always cut the 1st tree to the left and when I am at i-th tree, I check if prev value was 0,1,2 and accordingly I move forward. And I cut the last tree to the right
Hii, in the line 47 use this : "if(p[i].first-p[i].second>p[i-1].first+p[i-1].second) x=func(i+1,1);" instead of: "if(p[i].first-p[i].second>p[i-1].first+p[i].second) x=func(i+1,1);".
Not sure... what did I do wrong here http://codeforces.com/contest/545/submission/11155373
Getting WA on 5th test case for E problem. Does someone have an idea what is wrong with my code? Or maybe I can somehow view input of 5th test case :-) ? http://codeforces.com/contest/545/submission/11175222
I've managed to get AC on problem E. But I'm still confused and don't understand one fact. These are 2 solutions:
http://codeforces.com/contest/545/submission/11195293 (WA on 5th test case)
http://codeforces.com/contest/545/submission/11195260 (AC)
The difference is only in 1 line (line #40)
vs
Can someone explain me why does its really matter?
if you don't compare v and o.v when distance is equal, vertiсes (5, 0) and (5, 1) are equal
Exactly. But why is it a problem? They will be processed both in some order
TreeSet<Vertex> qif you insert (5, 0) and after it (5, 1), it will not be added. I think you don't want such behavior
No, it seems that set will contain both because vertices are not really equal. (compareTo == 0 isn't the same as equals == true)
no
Yes, you're right :-) Thank you very much for help!
hi, can anyone explain where i went wrong for 545b problem , link is http://codeforces.com/contest/545/submission/11158712 ,,,,, what i done is ,if the no of mismatch positions are odd then cout<<"impossible" else im flipping the first half of mismatch bits of first string and displaying it.
char ...n; It's wrong. You need n up to 10^5, it should be int.
Why am I getting WA in my solution ? I have covered all possible cases seland
http://codeforces.com/contest/545/submission/11184421
Maybe this can help you:
4
1 1
2 2
6 2
7 1
The answer is 3 while your answer is 4.
I think that for this test case ,
1st tree fell left, 2nd tree fell right, 3rd — left ( it can fall left ) , 4th — right
==> all 4 fell Please check phfvtm060
Sorry , I just forgot this case
If 2nd fell right, it'll take [2, 4] and 3rd fell left, it'll take [4, 6], which overlapped 2nd. So the answer is 3.
I tried to solve the problems after the contest and is successful for three(solved one during contest) and for 545E — Paths and Trees I am getting wrong answer on test 8. Here is my source http://codeforces.com/contest/545/submission/11186979 can someone help me where does it go wrong?
I debugged and found an overflow.
"It's true, that Dijkstra modification, where in case of equal distances we take one with shorter last edge, find an answer." Why do we take the shorter last edge in case of equal distances? No matter what edge we choose, it leads to shortest distance from source to that vertex. I don't see how this affects the weight of the shortest path tree. Any test case where not choosing shorter last edge fails?
The one from problem statement with 3 vertices
there is another solution for E where u can run dijkstra on the graph from u , then sort the nodes by distances , then add each node to the tree for further details check this out 11271206
I think it is the same solution
Hi anyone can please tell me why my code is getting memory limit exceed? It passes much larger cases but get memory limit exceed in a small case! My submitted code For E. Thanks.
Found it. When only updating the smallest weight no need to push into the queue again.
Even After reading the solution I thought of implementing a solution for problem C Could not find why it is wrong. TLE ok it can come as the answer is m*n may be
submission
The strategy I have implemented is
All the students attack the problem from the front. For each block ai student remain and the rest go forward and go to the next state. If a[i]>students arrived at the spot then all the student stay and remove until a[i]<less then the students the student start to pass to the next tasks.
I got wrong answer on 4th test case but could not figure out why any help would be appreciable
For the E question cant we just add the nodes in the order the that they get popped from the priority queue as this will ensure that sum of distances is also the least. Please correct me if wrong :)
The editorial for the problem C says:
__ Also this problem can be solved by the next greedy algorithm. Let's fell leftmost tree to the left (it always doesn't make an answer worse). After that, try to fell the next tree. If we can fell it to the left, let's do it (because it also always doesn't make an answer worse). If we can't, then try to fell it to the right. If it is possible, let's do it. Last step is correct because felling some tree to the right may only prevent the next tree's fallen. So we may "exchange" one tree to another without worsing an answer.
If we follows this approach then for the following:
13
5 9
16 10
24 7
30 5
34 3
36 1
would be 3 bu isn't the correct answer 6? (Fell all trees except the second one)
number of trees = 13 . You only printed 6 of them .
Guys, I didn't understand the DP solution of problem C ... Can anyone help ?
So, the idea is that you have these three DP arrays stay, left and right and you have that:
. Finally, you answer is given by max(stayn, leftn, rightn).
I hope that was good enough for you. If not, don't hesitate to ask more questions.
Thanks a lot!
Here is my solution for Div 2 — C using Top-Down DP/Memoization. 44734044
Not able to understand why greedy is giving AC.
In case tree fall in right direction then it may cover more than 1 trees right ?. Which will lead to bad result
It cant cover more than 1 tree, because even if it is covering the coordinate of first right tree, we can't make it fall on the right (thus not counting this in our answer). In fact, it can't cover any tree. Thus at worst case, we will be taking possible left "fall" of right tree, if we make the tree fell to its right (but its ok, since at the expense of 1 right tree, we are increasing the answer by 1).
vovuh could you plz explain your DP approach of 3rd problem
There's a typo in the editorial of problem E.
"egde" -> "edge"
bottom up solution for C : https://codeforces.com/contest/545/submission/226213472