548A - Mike and Fax
Consider characters of this string are number 0-based from left to right. If |s| is not a multiply of k, then answer is "NO". Otherwise, let 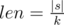 . Then answer is "Yes" if and only if for each i that 0 ≤ i < |s|, si = s(i / len) * len + len - 1 - (i%len) where a%b is the remainder of dividing a by b.
. Then answer is "Yes" if and only if for each i that 0 ≤ i < |s|, si = s(i / len) * len + len - 1 - (i%len) where a%b is the remainder of dividing a by b.

Time complexity: 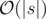 .
.
548B - Mike and Fun
Consider this problem: We have a binary sequence s and want to find the maximum number of consecutive 1s in it. How to solve this? Easily:
ans = 0
cur = 0
for i = 1 to n:
if s[i] == 0
then cur = 0
else
cur = cur + 1
ans = max(ans, cur)

Finally, answer to this problem is ans. For each row r of the table, let ansr be the maximum number of consecutive 1s in it (we know how to calculate it in O(m) right ?). So after each query, update ansi in O(m) and then find max(ans1, ans2, ..., ansn) in O(n).
Time complexity: 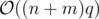
547A - Mike and Frog
In this editorial, consider p = m, a = h1, a′ = a1, b = h2 and b′ = a2, x = x1, y = y1, X = x2 and Y = y2.
First of all, find the number of seconds it takes until height of Xaniar becomes a′ (starting from a) and call it q. Please note that q ≤ p and if we don't reach a′ after p seconds, then answer is - 1.
If after q seconds also height of Abol will become equal to b′ then answer if q.
Otherwise, find the height of Abdol after q seconds and call it e.
Then find the number of seconds it takes until height of Xaniar becomes a′ (starting from a′) and call it c. Please note that c ≤ p and if we don't reach a′ after p seconds, then answer is - 1.
if g(x) = Xx + Y, then find f(x) = g(g(...(g(x)))) (c times). It is really easy:
c = 1, d = 0
for i = 1 to c
c = (cX) % p
d = (dX + Y) % p
Then,
f(x)
return (cx + d) % p

Actually, if height of Abol is x then, after c seconds it will be f(x).
Then, starting from e, find the minimum number of steps of performing e = f(e) it takes to reach b′ and call it o. Please note that o ≤ p and if we don't reach b′ after p seconds, then answer is - 1.
Then answer is x + c × o.
Time Complexity: 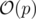
547B - Mike and Feet
For each i, find the largest j that aj < ai and show it by li (if there is no such j, then li = 0).
Also, find the smallest j that aj < ai and show it by ri (if there is no such j, then ri = n + 1).
This can be done in O(n) with a stack. Pseudo code of the first part (second part is also like that) :
stack s // initially empty
for i = 1 to n
while s is not empty and a[s.top()] >= a[i]
do s.pop()
if s is empty
then l[i] = 0
otherwise
l[i] = s.top()
s.push(i)

Consider that you are asked to print n integers, ans1, ans2, ..., ansn. Obviously, ans1 ≥ ans2 ≥ ... ≥ ansn.
For each i, we know that ai can be minimum element in groups of size 1, 2, ..., ri - li - 1.
Se we need a data structure for us to do this:
We have array ans1, ans2, ..., ansn and all its elements are initially equal to 0. Also, n queries. Each query gives x, val and want us to perform ans1 = max(ans1, val), ans2 = max(ans2, val), ..., ansx = max(ansx, val). We want the final array.
This can be done in O(n) with a maximum partial sum (keeping maximum instead of sum), read here for more information about partial sum.
Time complexity: 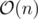 .
.
547C - Mike and Foam
We define that a number x is good if and only if there is no y > 1 that y2 is a divisor of x.
Also, we define function f(x) as follow:
Consider x = p1a1 × p2a2 × ... × pkak where all pis are prime. Then, f(x) = a1 + a2 + ... + an.
Use simple inclusion. Consider all the primes from 1 to 5 × 105 are p1, p2, ..., pk.
So, after each query, if d(x) is the set of beers like i in the shelf that x is a divisor of ai, then number of pairs with gcd equal to 1 is: 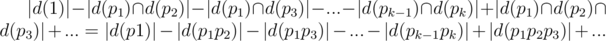
Consider good numbers from 1 to 5 × 105 are b1, b2, ..., bm. The above phrase can be written in some other way: |d(b1)| × ( - 1)f(b1) + |d(b2)| × ( - 1)f(b2) + ... + |d(bm)| × ( - 1)f(bm).
So, for each query if we can find all good numbers that ai is divisible by them in a fast way, we can solve the rest of the problem easily (for each good number x, we can store |d(x)| in an array and just update this array and update the answer).

Since all numbers are less than 2 × 3 × 5 × 7 × 11 × 13 × 17, then there are at most 6 primes divisible buy ai. With a simple preprocesses, we can find their maximum and so easily we can find these (at most 6) primes fast. If their amount is x, then there are exactly 2x good numbers that ai is divisible by them (power of each prime should be either 0 or 1).
So we can perform each query in O(26)
Time complexity: 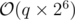 .
.
547D - Mike and Fish
Consider a bipartite graph. In each part (we call them first and second part) there are L = 2 × 105 vertices numbered from 1 to L. For each point (x, y) add an edge between vertex number x from the first part and vertex number y from the second part.
In this problem, we want to color edges with two colors so that the difference between the number of blue edges connected to a vertex and the number of red edges connected to it be at most 1.
Doing such thing is always possible.
We prove this and solve the problem at the same time with induction on the number of edges :

If all vertices have even degree, then for each component there is an Eulerian circuit, find it and color the edges alternatively_ with blue and red. Because graph is bipartite, then our circuit is an even walk and so, the difference between the number of blue and red edges connected to a vertex will be 0.
Otherwise, if a vertex like v has odd degree, consider a vertex like u that there is and edge between v and u. Delete this edge and solve the problem for the rest of the edges (with the induction definition) and then add this edge and if the number of red edges connected to u is more than the blue ones, then color this edge with blue, otherwise with red.
You can handle this add/delete edge requests and find odd vertices with a simple set. So,
Time complexity: 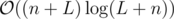
547E - Mike and Friends
call(i, j) = match(sjinsi) which match(tins) is the number of occurrences of t in s.
Concatenate all strings together in order (an put null character between them) and call it string S. We know that 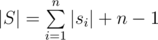 .
.
Consider N = 5 × 105. Consider Consider for each i, Sxisxi + 1...syi = si (xi + 1 = yi + 2).
Also, for i - th character of S which is not a null character, consider it belongs to swi.
Calculate the suffix array of S in 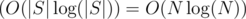 and show it by f1, f2, ..., f|S| (we show each suffix by the index of its beginning).
and show it by f1, f2, ..., f|S| (we show each suffix by the index of its beginning).
For each query, we want to know the number of occurrences of sk in Sxl...syr. For this propose, we can use this suffix array.
Consider that we show suffix of S starting from index x by S(x).
Also, for each i < |S|, calculate lcp(S(fi), S(fi + 1)) totally in 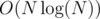 and show it by lci.
and show it by lci.

For each query, consider fi = xk, also find minimum number a and maximum number b (using binary search and sparse table on sequence lc) such that a ≤ i ≤ b and min(lca, lca + 1, ..., lci - 1) ≥ |sk| and min(lci, lci + 1, ..., lcb - 1) ≥ |sk|.
Finally answer of this query is the number of elements in wa, wa + 1, ..., wb that are in the interval [l, r].
This problem is just like KQUERY. You can read my offline approach for KQUERY here. It uses segment tree, but you can also use Fenwick instead of segment tree.
This wasn't my main approach. My main approach uses aho-corasick and a data structure I invented and named it C-Tree.
Time complexity: 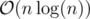
C++ Code by PrinceOfPersia (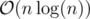 )
)
C++ Code by PrinceOfPersia (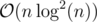 )
)
C++ Code by Haghani (Suffix array construction in 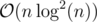 and the rest in
and the rest in 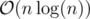 )
)

If there's any suggestion or error let me know.











Had another fun round, thanks for the problems.
I can't understand 5 pretest for B div2.What a pretest?
After system testing you will be able to see it under your code
I'm sure for my code. problem was easy
Can anybody explain why my code did't work 11303700
This part incorrect becouse if t<ans you don't reset it. If in the end of line t<ans your count for the next line would start not from 0 . Sorry for my awful english .
for(int j = 0; j < m ;j++) if(a[x][j] == 1)t++; else if(t > ans){ ^^^^^^^^^^^ ans = t; t = 0; ^^^^^^ } if(t > ans){ ans = t; try: for(int j = 0; j < m ;j++) {if(a[x][j] == 1) t++; else t=0; ans=max(ans,t);}
can't we use LCM in div2 C?
NO. Because suppose you get from 25 to 20 in 3 seconds. Now there is no guarantee that you'll get from 20 back to 20 in 3 seconds. It, in general,will take more/less time. Thus the concept of LCM fails.
Consider the nontrival case: cycle of h1 sequence including a1 found in [0, m] seconds is t1, cycle of h2 sequence including a2 found in [0, m] seconds is t2, h1 becomes a1 at pos1 seconds, h2 becomes a2 at pos2 seconds. Then I think LCM(t1, t2) or t1*t2 can be used if we start at pos0 = max(pos1, pos2) seconds when both cycles are "activated". Here is the lcm solution.
I think you only need to iterate from 0 to t2(or t1),instead of LCM(t1,t2).
In fact, I simply iterate [0, t2] in the old code because t1*t2 is the CM. Since LCM(t1, t2)/t1 = t2/gcd(t1,t2) <= t2, this implementation may be faster somewhat for some input.
Still not system tested and editorial is out, you're fast!
This is the fastest editorial, what I have seen! Thanks for a good contest!
My for E got TLE omg... 11288679
for E got TLE omg... 11288679
http://codeforces.com/contest/547/submission/11307115 swap(st[v], st[u]) -> O(st[v].size() + st[u].size()) st[v].swap(st[u]) -> O(1)
Unbelieveable... I thought it's working just like this swap. Also, had many problems AC before using swap(a, b)...
Most of them are overloaded. For example std set and map. But appearently it is not the case for order statistics tree.
Yeah, the swap function is a algorithm method in head file "algorithm". If we pass two containers to it, it maybe(depends on whether the function has been overloaded for the container) visit containers' each element then swap it. And the swap function of a container just swap the whole container(just swap the address containers' points point) in O(1) instead of their elements in O(size of container).
My O(nlog2n) for E got TLE. Sadly thing is, I always use
But today, I delete this line, because I think char s[N] will be better. Then I changed my mind.
Lesson 1 : Use ios..., if you're using cin and cout.
You may get TLE even using ios, if the number of queries is very high like 10^6 or something
You may get TLE even using Android.
Okey, really bad joke.
You may get TLE even using scanf. I just want to say, ios is important.
By the way, it reminds me of lower_bound. If we initial a set in C++, and insert a lot of elements, when we want to find the least one which is larger than x, lower_bound(s.begin(),s.end(),x),O(s.size()), s.lower_bound(x),O(log(s.size()))... The same as map in C++... I have struggled at this problem many times!
I overkilled B with segment trees -_- 11290242
I also used segment trees :D 11294974
Look at our source codes... "There are two types of people" :D
I used RMQ and binary search !!
Look at our source codes... "There are three types of people" :D
I used DSU)
segtree++
Hello,
Good contest, i have another answer for problem c but i couldnt get AC.
if we consider ( h1 * x1 + y1 ) % m then we can see that this falls in a loop so we can push each iteration in a vector and do the same for ( h2 * x2 + y2 ) % m if we name the vectors v1 and v2 respectively, if a1 and a2 do exist, we name their indices in v1 and v2, i and j respectively. now we want to find minimum p, q such that:
p*(sizeof(v1)) + i = j + q*(sizeof(v2))which is equal top*(sizeof(v1)) - q*(sizeof(v2)) = j - iand now ifj - i % gcd(sizeof(v1), -sizeof(v2)) != 0holds we output -1 else: the equation has infinite answers so we use Extended Euclidean Algorithm to find it.please correct me if im wrong.
Wow !!! che tasadofi !!! I honestly didn't read your comment and posted my own opinion but they are exactly the same o__O
Yep... Seems so!
I don't know what to say to make you believe but it's no big deal what you think.I really didn't even READ your comment before posting my comment.mifahmi?
dude chill... no hard feelings!:)
you right. But if x1, x2, y1, y2 ~ 10^5, then answer can be bigger 2*10^9. And in exgcd you not always have (x>0 && y>0) and this is very important.
Go on.
d1 — first day, when Xaniar have height a1. d2 — first day, when Abol have height a2.
l1 — length of cycle (a1->?->...->a1), and l2 — length of cycle (a2->?...->a2).
d1+x*l1 = d2+y*l2
x*l1 — y*l2 = d2 — d1
Use Extended Euclidean Algorithm and got answer
BUT!!!!
you can have test, when cycle a1->..->a1 doesn't exists. so you have h1->...->a1->...... So if answer exists it equals only d1 (It is only day, when Xaniar have height a1) So you check this answer.
I hope it's helpful
damn, you are right my cycles have bugs. i don't have the right cycle. i am really thankful.
no)
your gcdex give y < 0.
You have to get x > 0 && y > 0, or you can get negative number of day.
P.S. I'm glad you fixed bugs
that may be a problem too but if you look at my code filling the vectors you will notice that the supposed cycle i have isnt a cycle its something like
f1 -> f2 -> .. -> fi -> .. -> fn -> ... -> fi
and its wrong.
Thanks for helping me out.
Hey, can you explain why there would be a cycle at all? This is of the form f(f(x))%m, and I can't prove how there's a cycle being formed here at all
Well, I'm sure that there is a cycle, but not necessary a cycle with expected answer.
The prove is easy:
If we take (mod M) then there is a maximum of M different results (from 0 to M — 1). So after M + 1 iterations we'll got at least one number that was met before.
If the f(x) is a deterministic function — the whole sequence after that number would be the same as previous one.
Why does d2-d1 have to be the gcd of l1 and l2 ?
l1*x-l2*y=d2-d1
(l1*x-l2*y) % gcd(l1, l2) = 0 — I think, this is obvious (if not: suppose gcd(l1, l2)=g then l1 = k*g, l2 = l*g, and l1*x-l2*y = g*(kx-ly))
So (d2-d1) must be divided by gcd(l1, l2)
Hi
Can you please give a good link for studying Extended Euclidean Algo?
en.wikipedia.org/wiki/Extended_Euclidean_algorithm
I used this way to solve Div 2. C :we find the minimum time it takes for every one of the guys to reach its goal(I coded for this awfully). if one of them can't ever reach its goal (a1 and a2) so the answer is -1 otherwise (assume the distant of Xaniar to get to x is d1[x] and Abol d2[x]) the answer is the minimum number t1*m*d1[a1] for some non-negative value of t1 that is equal to t2*m*d2[a2] for some non-negative value of t2.So if d1[a1] is equal to d2[a2] we print it otherwise the answer is lowest common multiple of (m*d1[a1]) and (m*d2[a2]).After the contest finished I submitted this and got WA.Why's this wrong?
kmm = LCM = Least Common Multiple
No it's bmm :D
Yeah was a little mistake. sorry
Please someone respond.I'm pretty sure about MY approach.
In Problem A division 2 my submission failed at testcase 52 . But my logic is correct i just changed one line it got accepted .
11287822 Failed one
11306586 Accepted one
I think it is with string concatenation but why it is happenning.
The first argument to substr is the starting position and the second is the length of the substring. Ref: http://www.cplusplus.com/reference/string/string/substr/
problem C div.2 was one of the trickiest problems i've seen only 270 people from div.1 solved it!
I think I have an even simpler solution to D. 11307013
There is another way to find the largest j: a[j] < a[i]. Denote it by pos[i], then for every position do the following algorithm: pos[i] = i — 1, while (a[pos[i]] >= a[i]) pos[i] = pos[pos[i]]. I don't know why but it seems to work in linear time.
This round was a great challenge, keep it like this !
I used a RMQ with a Sparse Table for 547B - Mike and Feet, but without success. Someone thought the same?
I am afraid Sparse Table doesn't really help in this problem.see zt5840's commenti also used sparse table
This problem can be solved by ST and binary search. Link to my code: http://codeforces.com/contest/547/submission/11312230.
it can be solved by sparse table without binary search too (with two pointers)
Could be the problem Mike and Feet (Div 1 B / Div 2 D) be resolved using a dynamic programming approach?.
Also, I couldn't understand why for the test input, the solution for the group of size 2 was 4 and not 5. Shouldn't it be the strongest group of size 2 the one that contains the bears 6 and 5?
This is the sample test data: 10 1 2 3 4 5 4 3 2 1 6
Output: 6 4 4 3 3 2 2 1 1 1
Why the second number is 4? (group of size 2).
Groups should be contiguous subsequences. The sequences of length 2 including 5 are [4, 5] and [5, 4].
hi...can explain wat is in the editorial for the mike and feet problem...i understood till finding l[],r[]... after tat can u make it a bit clear...
You can open my submission (I think that it is readable enought) and follow the steps:
1) I compress the input array so that all integers are not greater than N and I denote the number of different integers with the variable "all". For example if we have the sequence 6,9,2,6, then it will become 2,3,1,2.
2) Make the observation that a number K can be the answer of the X-th query if there exists a contiguous subarray with length at least X in which K is the minimum number.
3) Find for each number what is the maximum contiguous subarray in which the minimum is that number using stack "s" and arrays "l" and "r".
4) Start with curr=all and put the current number as answer for the current query until it is possible, then decrease the current number.
A group of bears is a non-empty contiguous segment of the line.
Problem D can be solved with LR flow in bipartite graph, where first part corresponds to columns and second to rows. 11308635
What is LR flow?
It's algorithm to search flow, when each edge has not only maximum, but minimum capacity value too. So fe should satisfy Le ≤ fe ≤ Re.
Nice approach :like:
could you provide more information on your approach?
Can you find LR flow for general graph? Or just bipartite graph? Can you briefly explain the algo or maybe provide some links? Thank you very much :)
LR flow is literaly the first flow problem I have done (I just didn't hear that name), I'm sure you can come up with a solution to this (in general graph) in no time.
But could you explain solution of the problem from contest?
Firstly, if you're not aware with idea of points being edges in bipartite graph between vertices representing rows and columns then please read editorial. If you are, you can go along.
Assume that we push flow with vertices colored red. Than if we fix column c where there are 2k points then exactly k units of flow need to flow through this vertex and if there are 2k+1 points then k or k+1 units can go through this vertex which can be represented as conjunction of two inequalities — one being fc ≥ k and second fc ≤ k + 1. Analogously we treat case of 2k (k ≤ fc ≤ k) and analogously we treat rows.
In this article you can find method for general graph, it's simple enough.
Because circulation is actually a union of cycles?
It seems I don't use this fact.
I noticed that you do not even use lower capacities in your implementation.
After assuming there is a solution why would maximum flow guarantee this: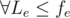
An alternative algorithm for Div1 A/Div2 C: 1) find the first time it takes to reach the target height and find the period (target height to target height) — these are t1,p1 and t2,p2 2) we need the minimum time when both will be at target height: thus, t1+ k1*p1 = t2 + k2*p2
(k2*p2)% p1 = (t1-t2)%p1;
So I tried all values of k2 from 0 to p1-1. The answer is t2 + k2*p2.
There are a few corner cases such as when p1 or p2 don't exist. You can look at my solution http://codeforces.com/contest/547/submission/11309426.
Caution: I was tired and I kept adding conditions till it passed. The code may still be incorrect. But it got accepted. The algorithm is probably correct :)
In DIV 2 prob B, according to constraints O(N*M*Q) should pass in 2s as :::: N*M*Q = 1.25 * (10^9). As generally O(10^9) solutions pass in 1s so the above solution should pass in 2s.
I want to know that how can one know if O(N*M*Q) will give TLE. It is quite easy to convert it to O((N+M)*Q) but how one knows if it O(N*M*Q) will give TLE. Plz guide me in this.
Please someone help me in this.
10^9 computations is not possible in 1s. In 1s, about 10^8(or 2*(10^8)) computations are maximally possible.
So what u want to emphasise is 10^8 computations is possible in 1s while 10^9 computations is possible in 2s
It depends on the type of computation you are doing. For example, 10^9 + or — or ifelse may pass in 2 seconds but if you are doing * or / or % then you might be in danger. If you really need to depend on such a solution, you can always try "custom invocation" to test how your solution acts on big tests (in CF of course).
i always thought xor and other bitwise operaters are faster than + or -
i would really want a table which shows what is faster and slower
I thought xor was way slower than & | operators. Seems i was wrong. Thanks for pointing out. I should have said % instead of ^. i'll update that comment
In Div2-D Mike and Feet, I don't understand the part which says "This can be done in O(n) with a maximum partial sum (keeping maximum instead of sum)". Can anybody explain this?
It is a simple variation of partial sum. If you understood partial sum via the linked document, you can understand this too:
First find the l[i] and r[i] for every 1<=i<=n. Code:
for(int i=1; i<=n; i++) // for l[] { while(!S.empty() && A[S.top()]>=A[i]) S.pop(); if(S.empty()) l[i]=0; else l[i]=S.top(); S.push(i); } for(int i=n; i>=1; i--) //for r[] { while(!T.empty() && A[T.top()]>=A[i]) T.pop(); if(T.empty()) r[i]=n+1; else r[i]=T.top(); T.push(i); }After this, first initialize the array ans[] with 0 as explained. Then, for every i from 1 to n, do this int p = r[i] — l[i] — 1. This will give you the interval in which A[i] is the mimimum. ans[p] = max(ans[p], A[i]). If A[i] is minimum than ans[p], then update the minimum of segment p with A[i].
So, here we are just updating ans[p] not the entire ans[] each time. Later we traverse once more from the last element to the first and update ans[i] with the maximum possible value. Here we make an observation that an element at i=5, ans[5] can also occur in i=1 to i=4.
for(int i=n-1; i>0; i--) ans[i]=max(ans[i],ans[i+1]);
It is little tricky but give it a try. Hope this helps.:)
My code: http://codeforces.com/contest/547/submission/11314560
Nice explanation, helpful :)
With reference to your last line of code
how do we make sure that ans[i] is not greater than max(ans[i],ans[i+1]) for all i
As per the editorial, it is given that ans[i]>=ans[i+1]. Also, in the above for loop we make sure that ans[i]>=ans[i+1] because we traverse from the end.
Thanks.. But consider a case when ans[i]<ans[i+1]..so we make ans[i]=ans[i+1] in the last line of code.. My question is why can't ans[i]>ans[i+1] as we have not calculated ans[i(len)] for every pair i,j where abs(i-j)+1 =len
thanks for your explanation but I still don't understand why r[i] — l[i] — 1 would give the internals in which A[i] is the minimum. Can you explain? More importantly, why would someone think about this problem in this way? I mean for me I wouldn't think about solving this problem anywhere near in this direction (e.g. first find array l, then find array r and then do r[i] — l[i] -1). Not to mention this is just the beginning of the whole procedure. I have spent a lot of time trying to understand the solution; I hope to understand why people would think in this way so that I can solve similar problems applying the same principle.
Hope my question makes sense. Thanks.
let j=l[i]. It is the largest position less than i such that A[j]<A[i]. It means that A[i] is minimum in the range j+1 to i. That is, from l[i]+1 to i.
Similarly, k=r[i] is the smallest position greater than i such that A[k]<A[i]. It means A[i] is minimum in the range i to r[i]-1.
Combining these two, we get A[i] is minimum in the range l[i]+1 to r[i]-1. And the length of the range is r[i]-l[i]-1.
As far as your second question is concerned, even I don't know, why would someone think in this manner. But I think, by practicing more questions, you get the intuition of solving it. If you have understood the problem and the solution, it will definitely help you.
Hope this helps.:)
thanks for this but I think you meant to say j is the max position such that A[j] < A[i] and k is the min position such that A[k] < A[i].
Not sure whether you made this obvious error on purpose to test my understanding:)
Yeah, I corrected the error. It was a mistake. Thanks.
another solution for DIV1B in O(n log* n) using DSU
code: 11289460
Can you please explain your solution ?
hard to explain!! :D
we have a graph with n(0 ... n — 1) vertices and n — 1 edges!
edges are between i and i + 1 with weight min(a[i], a[i + 1]) for all 0 <= i < n — 1
sort edges in descending order (now I know that it is O(n log n) :D)
now add edges one by one and each time:(step i) join these two sets! ans[size[that set]] = weight[i]
we know that if we have a set of size x with ans[x] we have a set of size y (y < x) of size at least ans[x]
and we know that ans[1] >= ans[2] >= ... >= ans[n]
now we go from n to 1 and do this ans[x] = max(ans[x], ans[x + 1], ..., ans[n]) <=> ans[x] = max(ans[x], ans[x + 1])
Thank you for your explanation
Can we have more editorials that include source code?
I really benefited from that too. It helps me a ton, I enjoyed this editorial thoroughly.
I tried solving Div 1 D using the suggested solution, but it keeps failing on case 14. Maybe someone more experienced can comment on what goes wrong? 11310012
EDIT: Fixed it, I forgot the graph might consist of multiple components. Accepted now :) 11310079
Can somebody please explain the solution to A? I don't understand why it's correct, I just compared each segment of the string to its reverse.
It's actually the 'same' thing, but without having to reverse the string.
Assuming that the length of the string is a multiple of k, we know that the size of each palindrome is
len = |s| / k, right?We also know that each char of the original string belongs to exactly one of these palindromes, ok? So let's see which one: All characters from the 0-th char to the
len - 1-th one belong to the 0th palindrome, all characters from thelen-th char to the2 * len - 1belong to the 1st palindrome, ..., all characters from thex * lento(x+1) * len -1belong to the x-th palindrome.So, given a character index, we only have to divide it by
lenand it will be equal to the index of the palindrome that it belongs to.Now that we know which palindrome it belongs to, we have to know where it starts, so if each palindrome has length
len, it means the 0th starts at0, the 1st starts atlen, the 2nd at2*len, ..., the xth atx*len.So, for the ith character of the original string,
i / lengives the index of the palindrome it belongs to, and(i /len) * lengives us where this palindrome starts. And the end is the start plus the length minus one, so it is(i /len) * len + len - 1.i % lenis equal to the index of the ith char in that palindrome, if we consider it as a separate string, so if we have the string "abcdef" and k = 2, we can see that 'd' is the 0th character of the 1st 'substring', i.e. "def", which is the same as3 % 3, since 'd' is at position 3 and len is also 3.Now we need to know which character we have to compare
s[i]with. If we did that as a separate string it would be justs[len - 1 - i], that is, we subtract i from the end. But since we are doing that without separating the substring from the original string, we just have to compares[i]tos[end - index], and we have seen that:end = (i /len) * len + len - 1index = i % lenSo we get:
s[(i / len) * len + len - 1 - (i%len)], as the editorial says.If I haven't made myself clear, feel free to ask me =)
Great! dcms2
Excellent explanation, dcms2 .
wish i know english like you haha
If you look at the fastest solutions for problem Div1 D, you'll discover very easy linear solution. Don't look at my code though — it's probably harder to understand.
Hey, could you explain the idea? I couldn't get it from the codes I saw.
Thanks
Let's build a graph where vertices are input points and edges are segments connecting them. We build it in such a way that there are no more than 1 point with no adjacent vertical edges in every vertical line and no more than 1 point with no adjacent horizontal edges in every horizontal line, and also there are no points with two or more adjacent edges of the same type.
Now if we have X points on some line, there are exactly X/2 (rounded down) edges connecting them. Therefore by simply painting endpoints of every edge in different colors we will reach our goal.
How to prove that such painting is always possible? Graph which we build is bipartite. Every path in it is some sort of zigzag with no two adjacent edges of same (vertical/horizontal) type. This means that every cycle have even length. And this is sufficient condition for graph being bipartite.
Got it, thanks!
Can anyone tell the condition after which we will be sure that the height of frog and flower will never be equal? Also will there be no limit on no. of iterations after which i can say that their height never equals?
I am not sure if there exist a limit to number of iterations after which we could say that height can never be equal. But if at all the limit exist, it must be large enough that we can't iterate.
Example-consider the test case-
999983 408725 408721 1 1 378562 294895 984270 0
Answer for which is 499981500166. Surely we can't iterate to that number
But i didn't understand the tutorial of this problem . Can you help me.
It's about finding cycles. When the solutions are too large it is because there are big cycles in both the frog and the plant. When we find the cycle for one of them we can know that after a number of seconds equal to the size of the cycle we will come to the same number.
Using this information we can go to the desired number for one of the 2 cycles and then just skip big amounts of seconds (the size of the cycle) to search the point where other number will become the desired. This search can be at most the size of the mod since when a number is repeated then we will repeat the same iterations.
Beautiful editorial, I hope everyone wrote editorials like this. I appreciate your work a lot.
I cannot get the DIV1-C inclusion equation.. I may not be familiar with problems like this yet. What's d(x) exactly? When {1,2,3,4,6} is in the shelf, I assumed d(1) to be {1,2,3,4,6} since 1 is a divisor of all
a_is.. But this gets far away from the answer. Can anyone explain this by an example?Hello !! We can reduce this problem to: Given a set of numbers , S = {a1,a2,...,an} y give a number x how many numbers in S there are , so that gcd(ai , x) == 1
so if express x = p1 * p2 * ... * pk , how the product of primes (unique) for example 60 = 2 * 2 * 3 * 5 -, but unique 60 = 2 * 3 * 5 if denote d(x) how the quantity of numbers divisible by x en S so the answer = d(1) — ( d(2) + d(3) + d(5) ) + ( d(2 * 3) + d(3 * 5) + d(2 * 5) ) — d(2 * 3 * 5)
d(1) = n (all number is divisible by 1) whicht is principe inclusion — exclusion !! I hope had help you!!
I understood everything up to the point you explain. But then the author does some jump which I am unable to follow, mainly how the same sum can be expressed differently in terms of bi's where bi is a good number.
So what exacly am I supposed to compute in terms of bi's for a given ai and why is the transformation from the inclusion-exclusion formula to the bi formula correct?
I feel like this editorial anwser is the perfect example where one has to dicipher half the anwser.
Can anyone explain the logic behind DSU solution for Div1 B?
Cant get DIV 2 D solution given in editorial. Can anyone explain it
See this
Can anyone explain Div1 C in detail? Sorry, but I don't understand anything from the editorial.
can any body explain the div2 C in a bit detail. what i was thinking is : calculate time in which h1 changes to a1 and then calculate time in which a1 changes again to a1.
but after that whole thing is getting messed up .
The idea is basically like this:
I think the code inside is confusing.. the variable name c is duplicated. Also, the final answer should have been
q+co, not including x..Well, that's much readable than editorial as for me, thanks.
@minsu the confusing thing is the time multiple of c when e becomes b'. please exlpain this step .
Well, it's obvious that a' becomes a' in multiple-of-c seconds. The next step is making e->b'. Iterating every c seconds, check if e becomes b'. f(x) is needed here for calculating the height after c seconds, when x is the initial height. Since there are only p possibilities of value, we try no more than p times. That's O(p). The pseudo-code might be:
This is the main algorithm, we also have to check all the exceptions..
Mike is really a cute bear!
Can anybody please explain Div1-C, I didn't get the editorial after reading it several times?
Huh, I just read D and I've seen this thing before: https://www.imo-official.org/year_info.aspx?year=1986
Q6 of IMO 1986. That's going back a while!
in problem A Div 1 i just don't get what happened in this part of the code
x[2] = x[1], y[2] = y[1]; x[1] = 1, y[1] = 0; do{ cur = nex(cur, 0); ++ o; x[1] = (1LL * x[1] * x[2]) % p; y[1] = (1LL * y[1] * x[2]) % p; y[1] = (1LL * y[1] + y[2]) % p; }while(o < p + 10 && cur != a[1]);
even though i solved it my way i don't get the editorial it is just so confusing if you can refine it a bit that would be helpful
For understanding Div1-C, Codechef-COPRIME3 did great help to me.
I didn't solve Div1B as it is explained in the article. Although it isn't really O(N), it's still nice, I guess.
First of all, I get the heights normalized. In the contest, I did it in O(NlogN), but, in order to obtain O(N), we can use radix-sort.
Then we can acces in O(1) the position of any height. Now let's have a look on the example:
10 1 2 3 4 5 4 3 2 1 6
Instead of finding out the maximum strenght among all groups of size x, we can find the minimum x for witch the answer is a certain height.
We take the heights in decreasing order and mark in an bool array its position. Using the example, we first mark 10th element. Then we mark the fifth, then we mark elements 4 and 6:
0 0 0 1 1 1 0 0 0 1
Because there are 3 consecutive marked elements, we know that for size 3 the answer is at least 4, the height we reached, and we remember this information in an array ans[x], the array we'll print.
So, for each height, we must know the largest sequence of marked elements. I used the union-find algorithm for this, wich works in O(log*N), which, in this universe, is O(1). I unite the new marked element with the sequence on its left and the sequence on its right, if they exist.It's source 11297991.
In the contest I solved this problem in O(Nlogn)(because heapsort, because .c), altough with radix-sort it would be O(Nlog*N), which is kind of O(N).
I wish to thank PrinceOfPersia for putting such an amazing effort into preparing the problem set and editorial. However, personally, the editorial is extremely difficult to understand in terms of language used/intent conveyed which is totally understandable since he is not a native speaker. Maybe, it would be a good idea to have a native English speaker vet through the editorial and modify it accordingly.
Hello everyone, I don't fully understand the explanation for the problem "Mike and Frog". The part I don't understand is the one below, any help would be much appreciated.
if g(x) = Xx + Y, then find f(x) = g(g(...(g(x)))) (c times). It is really easy:
c = 1, d = 0 for i = 1 to c c = (cX) % p d = (dX + Y) % p Then,
f(x) return (cx + d) % p
Why is the above true?
If g(x) = Xx + Y and you want to define a new function (f(x) = X'x + Y') that f(x) equals g(g(...g(x))) c times.
let's do it the hard way when c = 3
g(g(g(x))) = g(g(Xx + Y)) = g((X^2)x + XY + Y) = (X^3)x + (X^2)Y + XY + Y.
It's easy to observe that X' = (X^c), Y'= ((X^(c-1))Y + (X^(c-2))Y + ... + Y).
(sorry for my bad English .. and poor way of explanation :)
What are some corner case for Div1-A? I'm getting WA at test 26 but I don't know what did I do wrong.
In your case it is overflow in the output
printf("%d", i1-1);, i1 is long long, so you should print it as I64d or using cout.=)
Oh god, I made a very stupid mistake. Thanks!
you're welcome!
In 547B : isn't this better definition of li and ri: For each i, find the largest j, j<i that aj < ai and show it by li (if there is no such j, then li = 0). Also, find the smallest j, j>i that aj < ai and show it by ri (if there is no such j, then ri = n + 1).
Yours is the perfect definition. I had hard time understanding the tutorial. Hope the tutorial will be edited.
I tried to solve D (div 1) and got TLE on test 13. I used vector<pair<int,int> > to memorize the graph and in the dfs function I was visiting the edges 11344840 . Then, I switched to multiset<pair<int,int> > to memorize the graph and in the dfs function I deleted the edges 11344905 . Surprisingly, it got AC, although the time complexity is somewhere around O(NlogN) because of the "find" and "erase" functions in the multimap. However, the TLE solution had O(N) time complexity and went slower. Can someone explain to me how did this happen?
First submission complexity is actually O(nm). Consider next test : triangles with one common vertex (let call it 1). First you do 1 iteration of cycle in
triangles with one common vertex (let call it 1). First you do 1 iteration of cycle in
dfs(1), then 3, then 5, and so on. Total complexity on such is O(n2) (it is not worst test though).To make this code O(n + m) you need keep n pointers to first not checked edge coming from every vertex and start cycle from it (basically, continue previous cycle, not starting it over).
Yes, you are right, my bad. Thank you!
Where can I find more about this new data structure?
It's not too new; It's like generalized kmp tree. Anyway, you can read my paper.
So is it simply suffix link tree from Aho-Corasick?..
Yep!
Thanks for your Editorial,the problems are fairly nice.
In the editorial of problem Div. 1 A Why should q <= p? Sorry if the ques is stupid
I solved div1A/div2C as a linear diophantine equation, but the corner cases were annoying:
My code: http://codeforces.com/contest/548/submission/11385163
In the div1 problem B, the editorial says
For each i, find the largest j that aj < ai and show it by li (if there is no such j, then li = 0).
Here it doesn't mention, the largest index j should be lower than index i.
Also, find the smallest j that aj < ai and show it by ri (if there is no such j, then ri = n + 1).
Here it doesn't mention, smallest index j should be greater than index i.
This gave me a hard time to understand the editorial. Hope the editorial will be edited.
Can someone tell me how did my solution get accepted for 548B — http://codeforces.com/contest/548/submission/11400460 . The complexity is q*n*m.
A great Editorial . Always a great pleasure reading POP's Editorials...Great Job... Really a useful one. Now I feel like I missed a Very Good Round.. Looking forward for ur future contests..
Could someone please explain "547C — Mike and Foam" with more detail? I (and several others) can't understand it from the editorial. Thanks in advance!
547E(div1.E) We can use Suffix tree && Chair tree(prefix persistence segment tree). By this we can solve this problem inline, and time is O(nlogn), space is O(nlogn). this is my C++ code[submission:11516303]
Agreed
I'm sorry, but what i do not correct in problem div1 C. Let, we have test : 2 2 6 7 1 2 So, after first quere we have d[1] = 1, d[2] = 1, d[3] = 1, d[6] = 1, and answer is 1 * ( - 1)0 + 1 * ( - 1)1 + 1 * ( - 1)1 + 1 * ( - 1)2 = 0. Ok, it is true. After second queue, we have d[1] = 2, d[2] = 1, d[3] = 1, d[6] = 1, d[7] = 1, and answer is 2 * ( - 1)0 + 1 * ( - 1)1 + 1 * ( - 1)1 + 1 * ( - 1)2 + 1 * ( - 1)1 = 0, but right answer is 1. Where is my mistake?
I am getting WA for problem A in 28 no testcase. My Code : http://ideone.com/w3lbkh Please anyone help me to find out the bug.
You should change this:
To this:
I changed it but again Wrong ans
I got accept by that code
I write a C++ code same as editorial for question 547B - Mike and Feet and accepted: link
what is the prove of using stack will give correct answer in problem B div1 ?
I didn't understand it :( .
You can search about the Stock span problem , the problem(Div 1B) uses the same approach
In the problem A of codeforces round #305(div 2) first test case saba 2 has a answer NO . I think it should be YES as saba can be written as a combination of two palindromic strings which are "s" and "aba" so shouldn't the answer be YES?
what is lcs in problem E
In problem D1 D,for the odd case what if after solving the problem by removing an edge u,v, u has more red edges and v has more blue edges.In this case no matter what color you put on the edge u,v the constraint is not satisfied. Can somebody explain ?
Problem $$$C$$$ can be solved with mobius! We can let $$$g[x]$$$ represent the number pairs of indices such that have a gcd which is divisible by $$$x$$$. By mobius inversion, our answer is:
Computing and updating $$$g$$$ is straight-forward: $$$g[x]$$$ is $$$\binom{a}{2}$$$, where $$$a$$$ is the number of numbers which are divisible by $$$x$$$.
141436383