Random Team Can any one please help me to find how minimum number of pair friends can be formed in this probem,i got the maximum part ,but not getting how to calculate minimum numbers of pairs of friends.
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/26/2024 03:51:38 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










If there are x guys in a team, this team will produce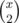 friends, so that means the number of friends we will have in the end will be
friends, so that means the number of friends we will have in the end will be
where xi is the number of guys in team i. If there's only one possible team (m = 1), we can't do nothing, so let's assume we have m > 1
Let's see what happens when we change one guy of his team (for instance, from team x2 to team x1. All terms will be equal except those of team 1 and 2, and it's gonna be better trade if our sum diminishes:
x2 > x1 + 1
this means we should take a guy from group 2 and put him in group 1 only if the number of guys in group 2 had at least 2 guys more than group 1. Based on that, we should try to keep the size of the groups as close as possible to minimize that sum.
for minimum number you would like to have equal number of people in all groups.so first you give n/m members to each team.now you will be left with n%m members.still what is the best way to ensure equality? you distribute these n%m members 1 per team in each of the arbitrarily selected n%m team . now why did we split in such a manner to ensure equality? we found that the number of friends is proportional to square of the number of people in a team. an intuitive example if we were to find to split 100 onto two parts such that the sum of squares is minimum we would split it in 50-50. ps- i recently did this question therefore got encouraged to share my approach . no disrespect to ivanilos sir :)
Thanks for the answers