Hello everyone. Here is problem I recently encountered on 'Algorithm and data structures' course exam. The problem statement is:
You are given a sequence a1,a2,...,an, and a number b. Your task is to find algorithm which counts all pairs (l,r) such that median of sequence a(l),a(l+1),..,a(r) is bigger than b.
My solution on exam was O(n^2logn) which used order statistics tree. Other solutions were
O(n^2) — used sorting to check median of pair in constant time
O(nlogn) — related to counting inverses in permutation.
And surprisingly someone came up with O(n) solution. So here is my question, can anyone tell me about this solution to the problem? I'm quite curious how this can be done in linear time.











Anywhere where I can submit this problem? I want to make sure solution is correct before I tell.
http://usaco.org/index.php?page=viewproblem2&cpid=91
solution
First, replace each element of sequence a with either -1 (if it's less than b) or 1 (otherwise). Now the problem becomes "find the number of subarrays of a such that the sum is nonnegative". Then, build a prefix sum array (make sure to have the leading 0). For each position from the 2nd position onwards in the prefix sum array, we want to count the number of elements preceding that and are less than or equal to the current element.
Already, if we use a BBST, we have a standard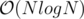 solution. To speed this up to
solution. To speed this up to  , notice that adjacent elements in our prefix sum array differ by at most 1. So we can use most of the information from the previous element, and we only need to consider three cases: our range is expanded by 1 (ai - 1 + 1 = ai), or it is decreased by 1 (ai - 1 - 1 = ai), or it stays the same (ai - 1 = ai). We should maintain a frequency table of "how many times the element x has occurred so far" for every x that occurs in the prefix sum array (the range is at most N because all the elements are either -1 or 1). With this information, we can easily update the count between adjacent indexes.
, notice that adjacent elements in our prefix sum array differ by at most 1. So we can use most of the information from the previous element, and we only need to consider three cases: our range is expanded by 1 (ai - 1 + 1 = ai), or it is decreased by 1 (ai - 1 - 1 = ai), or it stays the same (ai - 1 = ai). We should maintain a frequency table of "how many times the element x has occurred so far" for every x that occurs in the prefix sum array (the range is at most N because all the elements are either -1 or 1). With this information, we can easily update the count between adjacent indexes.
Wow, this is actually simpler than I thought. I guess i'd come up with nlogn solution if i thought about problem reduction, however this didn't really come to my mind.