A few days ago, someone much smarter than me shared with me the following problem. He said it involves "nothing else but simple arrays and for-loops, but has some weird observations to make". I couldn't solve it, even though the solution is simple enough that it can probably be understood by higher-rated pupils on CF. I thought it might be interesting to you, so here it is:
You are given an array $$$a$$$ with $$$n$$$ positive integers (you don't know anything about their maximum value). Find out the maximum difference between two elements if the array $$$a$$$ would be sorted.
Example:
Input: $$$n = 4, a = [11, 2, 7, 5]$$$
Output: $$$4$$$, because if we were to sort the array $$$a$$$, then we would have $$$[2, 5, 7, 11]$$$, so the maximum difference between two adjacent elements is $$$4$$$.
Of course, you can just sort the array in $$$O(n \log n)$$$ and find the difference that way. Value-based sorting (like radix sort) is not an option because you don't know what the maximum value is. But there is actually a way to find it in $$$O(n)$$$, without sorting the array.
Hope you enjoyed the problem!










https://leetcode.com/problems/maximum-gap/description/
https://csacademy.com/contest/interview-archive/task/consecutive-max-difference/
Cool! Now find minimum. Seriously though.
The idea with buckets is good. But you don't really have a good bound of the answer until you start calculating it.
Let's add elements one by one and maintain the answer and similar bucket structure. And let's set the bucket size to the current answer. The good thing about this structure is that each bucket contains at most one element, so when adding new element you only need to check the bucket with the element itself and two neighbouring ones, which takes $$$O(1)$$$ (keep buckets in a hash table to not waste anything on empty ones).
The bad thing is that the answer might change at some point and our structure stops being correct. Well, just rebuild it in linear time. "But that's quadratic" you might say. And you will be right, but what if we shuffle the array in the start? Then what is the probability that the newest element updates the answer? Well, since the answer have just been updated, the new distance is unique (or maybe you split some segment exactly in the middle, then not really unique, but that doesn't change much). So the new point must be one of the ends of this segment, and the probability of that is $$$\frac{2}{k}$$$, where $$$k$$$ is the number of processed elements (including the last one).
So, on $$$k$$$-th iteration you update the answer with probability $$$\frac{2}{k}$$$ and in that case rebuild everything in $$$O(k)$$$. So the expected time wasted on that iteration is $$$O(2)=O(1)$$$, which sums up to just $$$O(n)$$$.
... is that it works in spaces with more dimensions. Let's say you want to find 2 closest points in 3D. You do the same, except your buckets are cubes now (imagine cutting the space into a mesh with step d). It's not true that only one point will be at any bucket, but it's still $$$O(1)$$$ points. And you need to check your cube and all the neighbours, which is 27 buckets now. But technically it is still $$$O(n)$$$ in total.
I literally don't know the normal algorithm for the 2 closest points on a plane, because I have only used this one.
...I bet umnik uses binary search to find the bucket each point is in
I get the joke, but I can't just let it slide. The whole point is that it is $$$O(n)$$$.
This is famous interview problem: https://www.interviewbit.com/problems/maximum-consecutive-gap/
nice problem
it is wrong, think harder.
spitting this nonsense. I'm not if he used even a 1% of his brain power.
You probably just implemented it wrong lmao
sorry, I don't see how that solution is correct.
a = [5 2 1 4] sorted_a = [1 2 4 5] max = 5 second_max = 4 diff = 1 max_diff = 2 ???
found the guessforces expert
A mandatory pedantic comment
This is a horrible way to phrase it because you immediately proceed to contradict yourself:
Maybe you wanted to say that the radix sort has a pseudopolynomial complexity? However, this is not true, because its complexity is O(wn), where n is the number of keys, and w is the key length. It is polynomial because the input size is also O(wn).
Maybe you wanted to say that w is large, in which case O(wn) is polynomial but slow? However, your proposed solution also becomes slow if you account for the increasing cost of arithmetic operations. For example, subtraction becomes O(w), and division by n-1 may be even slower.
Maybe it's possible to construct a computational system where the complexities of primitive operations work out in favor of your proposed solution, but I doubt that it will be practical.
I think for $$$a_i \le 10^9,$$$ we can assume that the cost of such arithmetic operations is basically constant (because of word size), but it is not feasible to create an array of size $$$10^9$$$ in order to perform radix sort.
You can radix sort by the first bit, then by the second bit, etc. This way, you can sort 32-bit integers in 32 linear-time passes. (or be smarter and do 4 passes, each sorting by a group of 8 bits)
In general, you can sort $$$N$$$ numbers of $$$W$$$ bits in $$$O(WN)$$$ time.
I see. For some reason, I mistook radix sort for counting sort. 🤡
You must be thinking about counting sort, not radix sort.
Yes, I realized that later. I'm a clown
For me, it was pretty clear that he meant that you don't know the maximum value at the time of writing the program.
As if someone hardcodes key length in radix sort.
Well, radix sort wouldn't be significantly slower even with big numbers, but still. I agree with the things you said, but trying out both versions and measuring their runtime have more worth than talking about them.
Cool problem! I think there is a small mistake in your explanation.
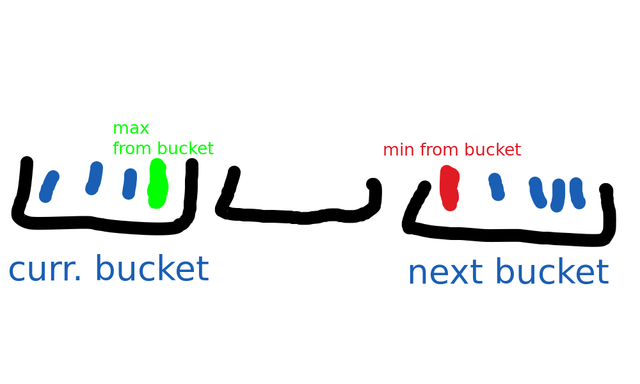
I though about the problem in a more "pigeonhole principle" type of way: Make N equally-sized buckets (this needs some adjusting when the $$$\max-\min+1$$$ doesn't divide $$$n$$$, but it still works).
If each element falls into a different bucket, we just sorted in linear time, so solve normally.
Otherwise, there are empty buckets, and the difference across an empty bucket will be bigger than any difference within a bucket, so the answer will be the $$$\min$$$ of a bucket minus the $$$\max$$$ of the previous non-empty bucket.
This brings me to what might be a mistake in your solution:
This is not an actual candidate (there can be 3 or more elements in the bucket), but checking it doesn't break the algorithm because one of two things always happens:
Totally not contradictory.
isn't this both not correct and unnecessary?
I agree, if the lower bound is the box size you never need to consider 2 elements from the same box. Also it would only be a valid candidate if the number of elements in the box were exactly 2.
Why this?
If you read the input array, you will definitely know the maximum value.
They are saying that it can be really large, so you can't use radix sort, because it takes $$$\mathcal{O(n \cdot \ell)}$$$. But as described in nskybytskyi's comment above, if the numbers are really quite large, the comparision and division operations described in this solution take $$$\mathcal{O(\ell)}$$$ time anyway (where $$$\ell$$$ is the length of the binary representation of the number).
What about using a vector containing ints (or lls) called values? Then, as you traverse the elements of the input array, you can set values[index]=value. Then, couldn't you just loop through 0 to n-1, and find the maximum value of the absolute value of (values[index+1]-values[index]), and output the max? Please let me know if I misunderstood the problem.