Recently IMO 2015 has ended. Problem 6 was the hardest one and solved by only 11 contestants, but for competitive programmers this task wasn't that hard. If you are interested in it, I think it's worth trying even if you haven't solved any IMO problems.
The problem statement is here.
I wrote some hints in white characters.
Hint 1: How is it related to competitive programming?
Hint 2: Doesn't it look like bitmask DP?
Hint 3: Run the following program.
mask = 0;
for(i=1;;i++){
mask» = 1;
mask| = (1«(ai - 1)); // here the newly set bit must be 0 before this operation
}
Hint 4: The number of '1' bits in mask is non-decreasing while the program is running.
So, the number of '1' bits will be constant at some moment: call it b.
Then, the sum of (aj - b) is the difference of sum of positions of set bits in mask when i = m and i = n.











rng_58 you should are both competitve programmer and mathematican :), great!
Of course. Check these links — 1 and 2. He perfected IMO once. One other similar guy that I know of is hos.lyric. Also, scott_wu got into IMO and IOI, but he didn't go to IMO or he would have got a gold there as well. There are plenty of other people who got into both IMO and IOI, like AstroConjecture, Dmitry_Egorov, semiexp, Swistakk, et cetera. But my favorite contestants ever are Reid Barton and bmerry. Another interesting phenomenon is Xellos. He got medals at IOI, IMO, IPhO, IChO, IAO, ILO, IZO, IPO, etc. Plus he has so much time to shitpost(he probably sleeps 2 hours a day) :D
And I am sharing lolcat pictures from Reddit :(
It seems that in Xellos's world duration of day is 100500 hours.
Nikolay Durov has 3 golds on IMO, 1 gold and 3 silvers on IOI and 2 titles in ACM ICPC
It should be mask>> = 1 shouldn't it ? That is you are right shifting after every iteration.
Yes, thank you, fixed.
So basically what you are saying is this:
In every iteration we definitely set one bit because of the condition a[i] + i != a[j] + j. This is because the set bit goes at position a[i] and after every subsequent iteration it moves right by 1, So its position after the kth iteration would be a[i] — k + i, and when a new bit is set a[i] — k + i != a[j] . Also after every iteration at most one bit goes away at the end, so the number of set bits is non-decreasing. At most 2015 bits can be set, so after a point it has to remain constant. At this point lets say there are b bits set in total. Now the last bit has to be set, because only then it gets removed after every iteration. Also when we set a[i]th bit we also move all the other set bits 1 step right. So the change in sum is actually a[i] — b. So the net change in sum of set bits is what is LHS. Also we can get maximum difference in sum for b = 1008, where we choose the initial sum to be 2015 + 2014 + 2013... + 1009 + 1 and the last sum is given by 1 + 2 +... + 1008, and the difference is 0 + 2013 + 2011 + .. + 1 = (1007)^2 !!!!
This maybe one of the most brilliant solution I have ever read !!
Thanks for sharing! The 2nd problem seems to be an interesting number-theoretical thing. Are there solutions anywhere?
Link. Go to the forum of needed problem.
Not sure why this should be easier for competitive programmers and bitmask DP looks for me like a last thing I would think of (maybe I will change my mind after few minutes of thinking), but for me it wasn't an obstacle to solve this problem in few minutes, because there is one other social group different than competitive programmers for which this problem should be really obvious. And this group is ... jugglers :).
Every juggler is well acknowledged with notion of siteswap. This is basically sequence of numbers denoting how high you need to throw a ball at given moments <=> when it will fall to your hand again (https://en.wikipedia.org/wiki/Siteswap ). See how condition ak + k ≠ al + l is relevant :)? Siteswaps are usually finite and we derive infinite ones by reapeating them. Every juggler also knows that arithmetic mean of numbers in siteswap is a number of used balls. So our sequence can be treated as an infinite siteswap and b should be a number of balls used to perform it. Solution to that problem is a slight modification of a proof of this classic AM statement (I didn't know this proof beforehand).
One has to also ask himself what is a "ball" in that problem? If we denote f(k) = ak + k then ball thrown at moment k shows again at moments f(k), f(f(k))... And they appear in moments k such that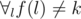 (that is, you don't have a ball which has just landed in your hand, but need to throw one up, so you need a new one). This is basically everything you need to know.
(that is, you don't have a ball which has just landed in your hand, but need to throw one up, so you need a new one). This is basically everything you need to know.
I think you just exactly described what is written/drawn on the paper in front of me.
Yes, I think in a similar way after the "call it b." part:
And there will be exactly b chains. The sum only depends on the tail / head of chains in (n, m]. And we know they can't be too far (>2014) from n and m. So it is easy to show the sum will be bounded by some number, like 2015^2, but showing it is 1007^2 will need some detailed calculation.