Hello every one
I've solved this problem but I have different questions about this problem:
The link : Frequent Values
The questions:
1 — How can I solve this problem if the values not sorted?
2 — How can I solve this problem online?
3 — How can I solve this problem if the values not sorted and online?
Edit: The link for the first question is here: values not sorted











First is Mo algorithm ...
Please explain how it can be done by Mo algorithm?
So for online method you can use BIT and make a new array b(b[i]=the numers of number from left of i with value a[i]).Now for query [L,R] take maximal from range :)
If values not sorted ,use Mo's algorithm.Read http://blog.anudeep2011.com/mos-algorithm/ . He has an example where he uses frequencies.U have to make the same but ,let's say we have an element with frequency x stored,we wanna keep an array and put 1 for every i(1<=i<=x).So in general,if you decrease the frequenct of an element from x to x-1,you decrease 1 at position x,if you increase,you increase 1 at position x+1.
Now for every query you binary search the last element in that array which is >0(hence there is a frequency existent).Or you can remove binary search and keep maximal 1 in the array,and update it when you decrease 1.
Total complexity O(N*sqrt(n)+Q*sqrt(n)+Q*log(n))) or O((N+Q)*sqrt(n)) The other solution is to keep a seg tree but it takes O(N*sqrt(n)+Q*sqrt(n)*log(n)),worse performane
For the 3rd problem,I wait myself for a solution...
Thanks for the link and explanation, but I have another question:
Is every problem solvable by BIT can be solved by Segment Tree?
BIT can be used for sum (in every case),and for maximal,minimal element when for a position ,every time you update the element,is better or equal than the previous value.Also can be used for multiplication when element is updated just once.
Seg tree can be used for a lot more things(gcd,multiplication-every time),lazy propagations,progressions,but it is more inefficient..
can you please provide some problems that needs Mo algorithm.
Yandex.Algorithm 2011 Round 2 Problem D
here: http://codeforces.com/problemset/problem/86/D
how did you solve this problem??using segment trees??
It's a RMQ problem, you can build the tree of the frequency of every value, so every query can be done by
O(log n), but you have to handle the corner cases whena[i] != a[j]so the answer is:So you have to keep track of the counter and the first appearance of every value.
For the third problem (online + arbitrary values):
Next idea is sqrt decomposition. For a fixed L we can calculate answers for all possible Rs in O(N) (just keeping current amount of occurrences for each number in an array). Unfortunately, we cannot precalculate answers for all segments (it would be O(N2), to let's do it for K uniformly distributed Ls, it will be O(NK).
Then, we have some queries incoming. Suppose we have query [L, R]. Then we know that we can "shift" L for not more than elements and get a precalculated query. With the power of point 3 we now can answer query in
elements and get a precalculated query. With the power of point 3 we now can answer query in 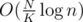 .
.
The only thing left is to chose K wisely. We can let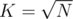 and have
and have 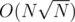 precalc and
precalc and  per query. Or we can minimize
per query. Or we can minimize 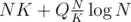 , where Q is amount of queries, and it's minimal when
, where Q is amount of queries, and it's minimal when 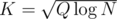 (just take a derivative). That way we have
(just take a derivative). That way we have 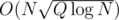 for precalculation and
for precalculation and 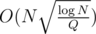 per query. When N ≈ Q we have
per query. When N ≈ Q we have  for precalc and
for precalc and 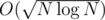 per query, which sums up to
per query, which sums up to 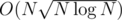
Also I want to add an approach which is based on this idea but is faster.Overall complexity O(N*k+Q*(n/k)).So you can choose k=sqrt(Q) for the best complexity.
You can find it in this editorial https://discuss.codechef.com/questions/66188/qchef-editorial ,it's big but not so hard. Even if there the problem wants something else, you can change the meaning of last[i][j] from last position of j to number of positions equal to j and it's all done.
Also this problem uses same approach. https://www.codechef.com/problems/QCHEF
Auto comment: topic has been updated by Mhammad1 (previous revision, new revision, compare).